2021-2022学年度人教版七年级数学下册课件 7.1.2 平面直角坐标系 (共22张PPT)
文档属性
| 名称 | 2021-2022学年度人教版七年级数学下册课件 7.1.2 平面直角坐标系 (共22张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-30 14:31:06 | ||
图片预览




文档简介
(共22张PPT)
第七章
平面直角坐标系
七年级数学人教版·下册
7.1.2 平面直角坐标系
授课人:XXXX
教学目标
1.平面直角坐标系和点的坐标;(重点)
2.根据点的位置写出点的坐标, 根据点的坐标描出点的位置.(难点)
新课导入
思考1: 如图, 数轴上的点 A, B 表示的数是什么?
表示数字4的点是哪个点?
0
1
2
3
4
-3
-2
-1
A
B
C
思考2 : 由(1)你发现数轴上的点与实数是什么关系?
一一对应.
①数轴上的每个点都对应一个实数(这个实数叫作这个
点在数轴上的坐标);
②反过来,知道一个数, 这个数在数轴上的位置就确定了.
A: -3; B: 2.
点C.
新课导入
数学家笛卡儿潜心研究能否用代数中的计算来代替几何中的证明. 有一天, 在梦中他用金钥匙打开了数学宫殿的大门, 遍地的珠子光彩夺目, 他看见窗框角上有一只蜘蛛正忙着结网, 顺着吐出的丝在空中飘动, 一个念头闪过脑际: 眼前这一条条的横线和竖线不正是自己全力研究的直线和曲线吗
1596-1650
新知探究
3
1
4
2
5
-2
-4
-1
-3
O
y
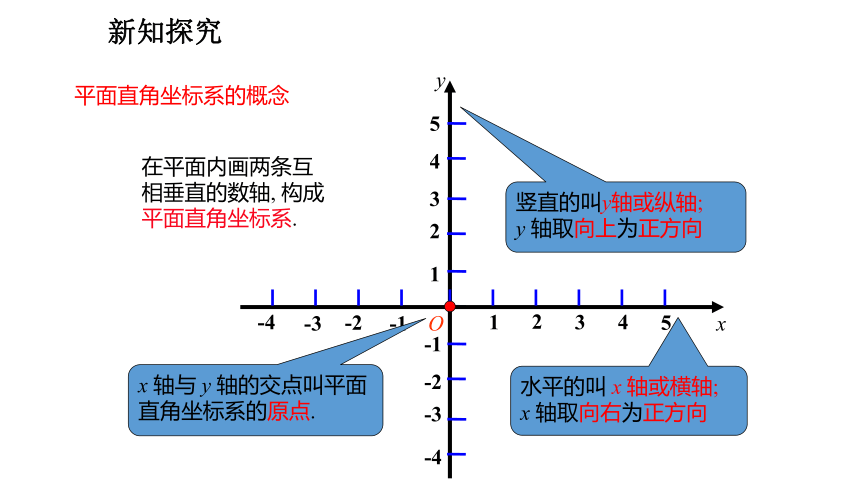
在平面内画两条互相垂直的数轴, 构成平面直角坐标系.
1
2
3
4
5
-4
-3
-2
-1
x
竖直的叫y轴或纵轴;
y 轴取向上为正方向
水平的叫 x 轴或横轴;
x 轴取向右为正方向
x 轴与 y 轴的交点叫平面直角坐标系的原点.
平面直角坐标系的概念
新知探究
2
-1
A
B
C
D
1
5
4
3
-4
-3
-2
-1
O
6
4
3
2
1
5
-2
-3
-4
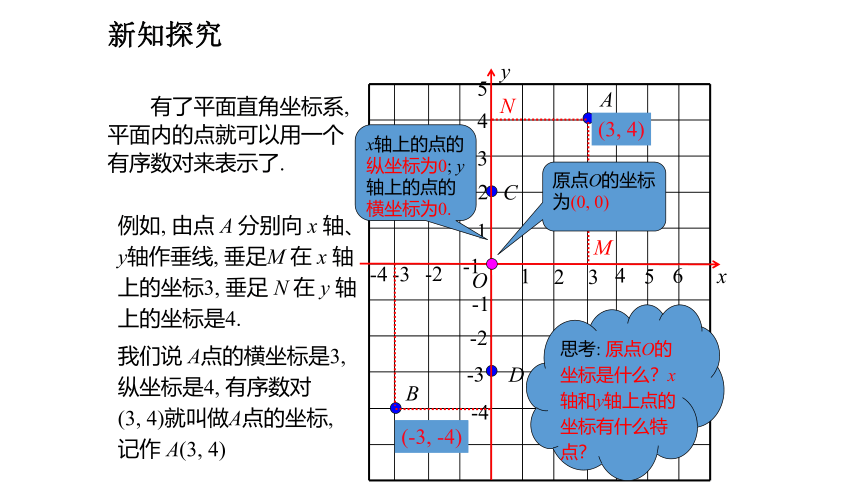
有了平面直角坐标系, 平面内的点就可以用一个有序数对来表示了.
x
y
例如, 由点 A 分别向 x 轴、y轴作垂线, 垂足M 在 x 轴上的坐标3, 垂足 N 在 y 轴上的坐标是4.
(3, 4)
我们说 A点的横坐标是3, 纵坐标是4, 有序数对
(3, 4)就叫做A点的坐标, 记作 A(3, 4)
M
N
(-3, -4)
思考: 原点O的坐标是什么?x轴和y轴上点的坐标有什么特点?
原点O的坐标为(0, 0)
x轴上的点的纵坐标为0; y轴上的点的横坐标为0.
新知探究
3
1
4
2
5
-2
-4
-1
-3
O
1
2
3
4
5
-4
-3
-2
-1
x
y
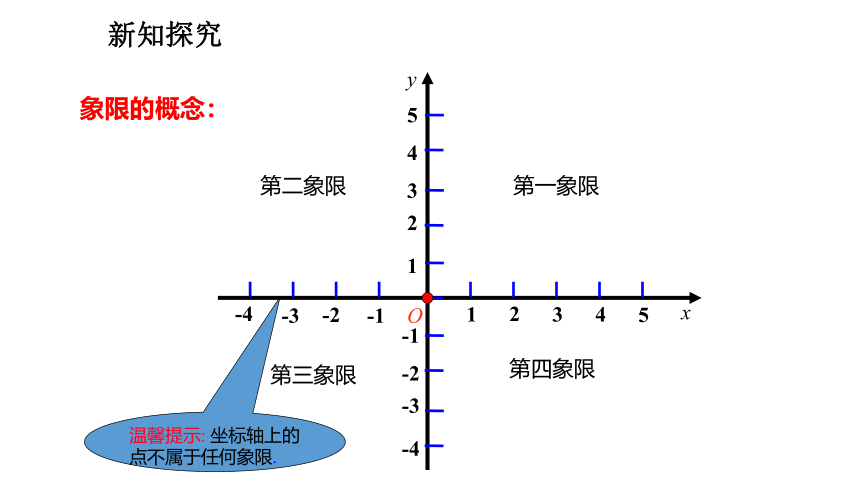
第一象限
第二象限
第三象限
第四象限
象限的概念:
温馨提示: 坐标轴上的点不属于任何象限.
新知探究
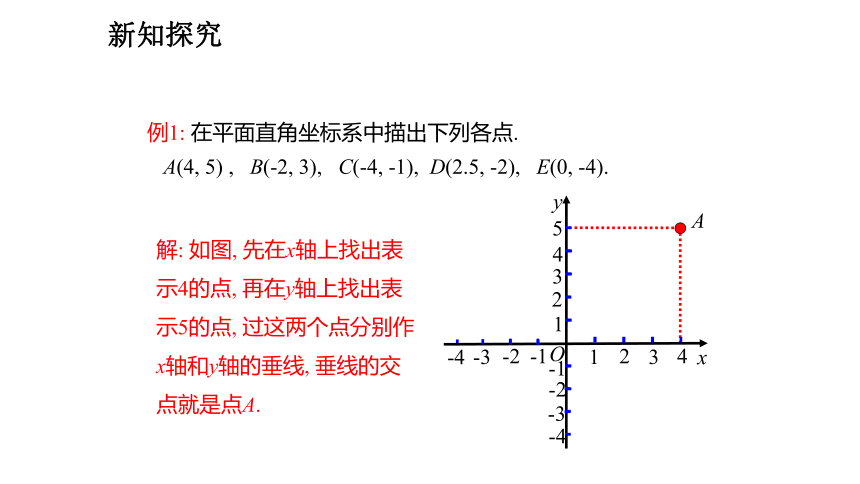
例1: 在平面直角坐标系中描出下列各点.
A(4, 5) , B(-2, 3), C(-4, -1), D(2.5, -2), E(0, -4).
A
解: 如图, 先在x轴上找出表示4的点, 再在y轴上找出表示5的点, 过这两个点分别作x轴和y轴的垂线, 垂线的交点就是点A.
y
O
x
-1
-2
-3
-1
-2
-3
-4
1
2
3
4
1
2
3
4
5
-4
新知探究
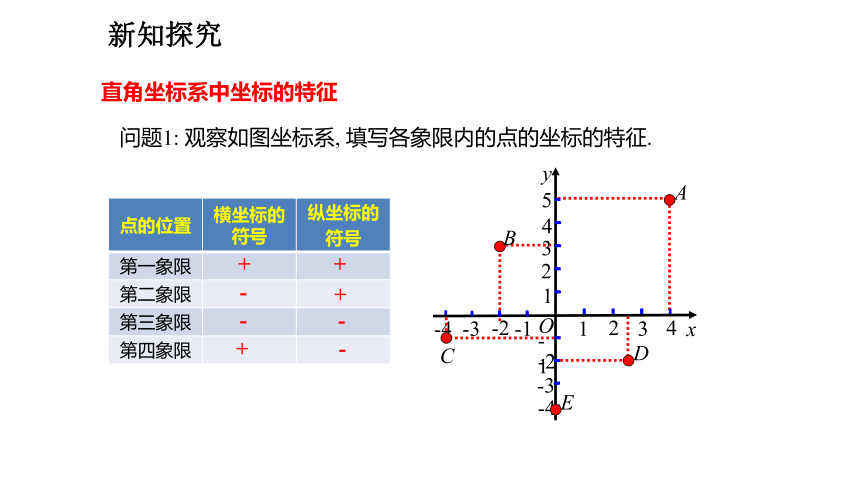
问题1: 观察如图坐标系, 填写各象限内的点的坐标的特征.
点的位置 横坐标的符号 纵坐标的
符号
第一象限
第二象限
第三象限
第四象限
+
+
+
-
-
-
+
-
A
y
O
x
-1
-2
-3
-1
-2
-3
-4
1
2
3
4
1
2
3
4
5
-4
B
C
D
E
直角坐标系中坐标的特征
新知探究
点的位置 横坐标的符号 纵坐标的
符号
在x轴的正半轴上
在x轴的负半轴上
在y轴的正半轴上
在y轴的负半轴上
0
+
+
-
-
0
0
0
A
y
O
x
-1
-2
-3
-1
-2
-3
-4
1
2
3
4
1
2
3
4
5
-4
B
C
D
E
问题2: 观察如图坐标系, 填写坐标轴上的点的坐标的特征.
知识归纳
①对于坐标平面内任意一点M, 都有唯一的一对有序实数(x, y) (即点M 的坐标)和它对应;
②反过来, 对于任意一对有序实数(x, y), 在坐标平面内都有唯一的一点M(即坐标为(x, y)的点)和它对应.
也就是说, 坐标平面内的点与有序实数对是一一对应的.
新知探究
(O) 1 2 3 4 5
6
5
4
3
2
1
例2: 正方形ABCD的边长为6 , 如果以点 A 为坐标原点, AB 所在直线为 x 轴, 建立平面直角坐标系, 那么 y 轴是哪条线?写出正方形的顶点 A, B, C, D的坐标.
D
A
B
C
(0, 0)
y
(6, 0)
(6, 6)
(0, 6)
新知探究
请另建立一个平面直角坐标系, 这时正方形的顶点A, B, C, D的坐标又分别是什么?与同学们交流一下.
D
A
B
C
x
y
(3,3)
(3,-3)
(-3,-3)
(-3,3)
新知探究
由上得知, 建立的平面直角坐标系不同, 则各点的坐标也不同. 你认为怎样建立直角坐标系才比较适当?
平面直角坐标系建立得适当, 可以容易确定图形上的点, 例如以正方形的两条边所在的直线为坐标轴, 建立平面直角坐标系. 又如按图建立平面直角坐标系. 建立不同的平面直角坐标系, 同一个点就会有不同的坐标, 但正方形的形状和性质不会改变.
新知探究
B(-4, 3)
1
2
3
-3
x
-2
·
-2
-3
o
-1
y
4
2
5
3
6
1
①(0 , 6), (-4, 3), (4 , 3)
②(-2 , 3), (-2 , -3), (2 , -3), (2 , 3)
·
·
·
·
·
·
-4
-1
4
C(4, 3)
D(-2, 3)
G(2, 3)
E(-2, -3)
F(2, -3)
A(0 , 6)
·
在如图建立的直角坐
标系中读出下列各点.
你能发现什么
新知探究
分别写出图中点 A, B, C, D 的坐标. 观察图形, 并回答问题.
(3, 2)
(3, -2)
-2
-1
4
3
2
1
-3
-4
-4
y
1
2
3
-3
-1
-2
(-3, 2)
(-3, -2)
O
点A与点B的位置有什么特点
点A与点B的坐标有什么关系
点A与点C 的位置有什么特点
点A与点C 的坐标有什么关系
点B与点C的位置有什么特点
点B与点C的坐标有什么关系
关于 x 轴对称的点的横坐标相同, 纵坐标互为相反数.
关于 y 轴对称的点的纵坐标相同, 横坐标互为相反数.
关于原点对称的点的横坐标、纵坐标都互为相反数.
A
B
C
D
课堂小结
平面直角坐标系
在平面内画两条互相垂直的数轴, 构成平面直角坐标系.
第一象限: (+, +), 第二象限: (-, +),
第三象限: (-, -), 第四象限: (+, -).
x轴上的点的纵坐标为0, 表示为(x, 0).
y轴上的点的横坐标为0, 表示为(0, y).
坐标平面内的点与有序实数对是一一对应的.
平面直角坐标系中的点关于. x轴, y轴, 原点对称的点的特点.
课堂小测
1.请你根据下列各点的坐标判定它们分别在第几象限或在什
么坐标轴上?
A(-5, 2) B (3, -2) C(0, 4) D(-6, 0)
E(1, 8) F(0, 0) G(5, 0) H(-6, -4)
第二象限
第四象限
y轴的正半轴上
x轴的负半轴上
第一象限
坐标原点
x轴的正半轴上
第三象限
课堂小测
2.在平面直角坐标系内,下列各点在第四象限的是( )
A.(2,1) B.(-2,1) C.(-3,-5) D.(3,-5)
D
3.已知坐标平面内点A(m, n)在第四象限, 那么点B(n, m)在 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
B
4.点(4, 3)与点(4,- 3)的关系是 ( )
A.关于原点对称 B.关于 x 轴对称 C.关于 y 轴对称 D.不能构成对称关系
B
课堂小测
5.点(3, -2)在第_____象限; 点(-1.5, -1)在第_______象限, 点(0, 3)在____轴上; 若点(a+1, -5)在 y 轴上, 则 a=______.
7.点 M (- 8, 12)到 x 轴的距离是_____, 到 y 轴的距离是______.
6.点 A在 x 轴上, 距离原点4个单位长度, 则 A点的坐标是____________.
三
y
-1
(4, 0)或(-4, 0)
12
8
四
课堂小测
8.方格纸上分别描出下列点的看看这些点在什么位置上, 由此你有什么发现?
-4 –3 –2 –1 o
1 2 3 4 5
-1
-2
-3
-4
x
y
A (2, 3)
B (2, -1)
C (2, 4)
D (2, 0)
E (2, -5)
F (2, -4)
A
B
D
E
F
C
●
●
●
●
●
●
横坐标相等的点在一条直线上且平行于 y 轴.
1
2
3
4
-5
第七章
平面直角坐标系
七年级数学人教版·下册
7.1.2 平面直角坐标系
授课人:XXXX
教学目标
1.平面直角坐标系和点的坐标;(重点)
2.根据点的位置写出点的坐标, 根据点的坐标描出点的位置.(难点)
新课导入
思考1: 如图, 数轴上的点 A, B 表示的数是什么?
表示数字4的点是哪个点?
0
1
2
3
4
-3
-2
-1
A
B
C
思考2 : 由(1)你发现数轴上的点与实数是什么关系?
一一对应.
①数轴上的每个点都对应一个实数(这个实数叫作这个
点在数轴上的坐标);
②反过来,知道一个数, 这个数在数轴上的位置就确定了.
A: -3; B: 2.
点C.
新课导入
数学家笛卡儿潜心研究能否用代数中的计算来代替几何中的证明. 有一天, 在梦中他用金钥匙打开了数学宫殿的大门, 遍地的珠子光彩夺目, 他看见窗框角上有一只蜘蛛正忙着结网, 顺着吐出的丝在空中飘动, 一个念头闪过脑际: 眼前这一条条的横线和竖线不正是自己全力研究的直线和曲线吗
1596-1650
新知探究
3
1
4
2
5
-2
-4
-1
-3
O
y
在平面内画两条互相垂直的数轴, 构成平面直角坐标系.
1
2
3
4
5
-4
-3
-2
-1
x
竖直的叫y轴或纵轴;
y 轴取向上为正方向
水平的叫 x 轴或横轴;
x 轴取向右为正方向
x 轴与 y 轴的交点叫平面直角坐标系的原点.
平面直角坐标系的概念
新知探究
2
-1
A
B
C
D
1
5
4
3
-4
-3
-2
-1
O
6
4
3
2
1
5
-2
-3
-4
有了平面直角坐标系, 平面内的点就可以用一个有序数对来表示了.
x
y
例如, 由点 A 分别向 x 轴、y轴作垂线, 垂足M 在 x 轴上的坐标3, 垂足 N 在 y 轴上的坐标是4.
(3, 4)
我们说 A点的横坐标是3, 纵坐标是4, 有序数对
(3, 4)就叫做A点的坐标, 记作 A(3, 4)
M
N
(-3, -4)
思考: 原点O的坐标是什么?x轴和y轴上点的坐标有什么特点?
原点O的坐标为(0, 0)
x轴上的点的纵坐标为0; y轴上的点的横坐标为0.
新知探究
3
1
4
2
5
-2
-4
-1
-3
O
1
2
3
4
5
-4
-3
-2
-1
x
y
第一象限
第二象限
第三象限
第四象限
象限的概念:
温馨提示: 坐标轴上的点不属于任何象限.
新知探究
例1: 在平面直角坐标系中描出下列各点.
A(4, 5) , B(-2, 3), C(-4, -1), D(2.5, -2), E(0, -4).
A
解: 如图, 先在x轴上找出表示4的点, 再在y轴上找出表示5的点, 过这两个点分别作x轴和y轴的垂线, 垂线的交点就是点A.
y
O
x
-1
-2
-3
-1
-2
-3
-4
1
2
3
4
1
2
3
4
5
-4
新知探究
问题1: 观察如图坐标系, 填写各象限内的点的坐标的特征.
点的位置 横坐标的符号 纵坐标的
符号
第一象限
第二象限
第三象限
第四象限
+
+
+
-
-
-
+
-
A
y
O
x
-1
-2
-3
-1
-2
-3
-4
1
2
3
4
1
2
3
4
5
-4
B
C
D
E
直角坐标系中坐标的特征
新知探究
点的位置 横坐标的符号 纵坐标的
符号
在x轴的正半轴上
在x轴的负半轴上
在y轴的正半轴上
在y轴的负半轴上
0
+
+
-
-
0
0
0
A
y
O
x
-1
-2
-3
-1
-2
-3
-4
1
2
3
4
1
2
3
4
5
-4
B
C
D
E
问题2: 观察如图坐标系, 填写坐标轴上的点的坐标的特征.
知识归纳
①对于坐标平面内任意一点M, 都有唯一的一对有序实数(x, y) (即点M 的坐标)和它对应;
②反过来, 对于任意一对有序实数(x, y), 在坐标平面内都有唯一的一点M(即坐标为(x, y)的点)和它对应.
也就是说, 坐标平面内的点与有序实数对是一一对应的.
新知探究
(O) 1 2 3 4 5
6
5
4
3
2
1
例2: 正方形ABCD的边长为6 , 如果以点 A 为坐标原点, AB 所在直线为 x 轴, 建立平面直角坐标系, 那么 y 轴是哪条线?写出正方形的顶点 A, B, C, D的坐标.
D
A
B
C
(0, 0)
y
(6, 0)
(6, 6)
(0, 6)
新知探究
请另建立一个平面直角坐标系, 这时正方形的顶点A, B, C, D的坐标又分别是什么?与同学们交流一下.
D
A
B
C
x
y
(3,3)
(3,-3)
(-3,-3)
(-3,3)
新知探究
由上得知, 建立的平面直角坐标系不同, 则各点的坐标也不同. 你认为怎样建立直角坐标系才比较适当?
平面直角坐标系建立得适当, 可以容易确定图形上的点, 例如以正方形的两条边所在的直线为坐标轴, 建立平面直角坐标系. 又如按图建立平面直角坐标系. 建立不同的平面直角坐标系, 同一个点就会有不同的坐标, 但正方形的形状和性质不会改变.
新知探究
B(-4, 3)
1
2
3
-3
x
-2
·
-2
-3
o
-1
y
4
2
5
3
6
1
①(0 , 6), (-4, 3), (4 , 3)
②(-2 , 3), (-2 , -3), (2 , -3), (2 , 3)
·
·
·
·
·
·
-4
-1
4
C(4, 3)
D(-2, 3)
G(2, 3)
E(-2, -3)
F(2, -3)
A(0 , 6)
·
在如图建立的直角坐
标系中读出下列各点.
你能发现什么
新知探究
分别写出图中点 A, B, C, D 的坐标. 观察图形, 并回答问题.
(3, 2)
(3, -2)
-2
-1
4
3
2
1
-3
-4
-4
y
1
2
3
-3
-1
-2
(-3, 2)
(-3, -2)
O
点A与点B的位置有什么特点
点A与点B的坐标有什么关系
点A与点C 的位置有什么特点
点A与点C 的坐标有什么关系
点B与点C的位置有什么特点
点B与点C的坐标有什么关系
关于 x 轴对称的点的横坐标相同, 纵坐标互为相反数.
关于 y 轴对称的点的纵坐标相同, 横坐标互为相反数.
关于原点对称的点的横坐标、纵坐标都互为相反数.
A
B
C
D
课堂小结
平面直角坐标系
在平面内画两条互相垂直的数轴, 构成平面直角坐标系.
第一象限: (+, +), 第二象限: (-, +),
第三象限: (-, -), 第四象限: (+, -).
x轴上的点的纵坐标为0, 表示为(x, 0).
y轴上的点的横坐标为0, 表示为(0, y).
坐标平面内的点与有序实数对是一一对应的.
平面直角坐标系中的点关于. x轴, y轴, 原点对称的点的特点.
课堂小测
1.请你根据下列各点的坐标判定它们分别在第几象限或在什
么坐标轴上?
A(-5, 2) B (3, -2) C(0, 4) D(-6, 0)
E(1, 8) F(0, 0) G(5, 0) H(-6, -4)
第二象限
第四象限
y轴的正半轴上
x轴的负半轴上
第一象限
坐标原点
x轴的正半轴上
第三象限
课堂小测
2.在平面直角坐标系内,下列各点在第四象限的是( )
A.(2,1) B.(-2,1) C.(-3,-5) D.(3,-5)
D
3.已知坐标平面内点A(m, n)在第四象限, 那么点B(n, m)在 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
B
4.点(4, 3)与点(4,- 3)的关系是 ( )
A.关于原点对称 B.关于 x 轴对称 C.关于 y 轴对称 D.不能构成对称关系
B
课堂小测
5.点(3, -2)在第_____象限; 点(-1.5, -1)在第_______象限, 点(0, 3)在____轴上; 若点(a+1, -5)在 y 轴上, 则 a=______.
7.点 M (- 8, 12)到 x 轴的距离是_____, 到 y 轴的距离是______.
6.点 A在 x 轴上, 距离原点4个单位长度, 则 A点的坐标是____________.
三
y
-1
(4, 0)或(-4, 0)
12
8
四
课堂小测
8.方格纸上分别描出下列点的看看这些点在什么位置上, 由此你有什么发现?
-4 –3 –2 –1 o
1 2 3 4 5
-1
-2
-3
-4
x
y
A (2, 3)
B (2, -1)
C (2, 4)
D (2, 0)
E (2, -5)
F (2, -4)
A
B
D
E
F
C
●
●
●
●
●
●
横坐标相等的点在一条直线上且平行于 y 轴.
1
2
3
4
-5
