2021-2022学年度人教版七年级数学下册8.3 实际问题与二元一次方程组课件(共24张PPT)
文档属性
| 名称 | 2021-2022学年度人教版七年级数学下册8.3 实际问题与二元一次方程组课件(共24张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-30 14:39:42 | ||
图片预览








文档简介
(共24张PPT)
七年级数学人教版·下册
8.3.1 用二元一次方程组解决数字,
和、差、倍、分等问题
授课人:XXXX
第八章
二元一次方程组
教学目标
1.以方程组为工具, 分析、解决含有多个未知数的实际问题;(重点)
2.确定解题策略, 二元一次方程组解决数字, 和、差、倍、分等问题.
(难点)
新课导入
-3
-1
2
新知探究
例1:一个两位数, 十位上的数字比个位上的数字大5, 如果把十位上的数
字与个位上的数字交换位置, 那么得到的新两位数比原来的两位数
的一半还少9, 求这个两位数?
解:设个位上的数字为 x, 十位上的数字为 y. 根据题意得
答:这个两位数是72.
.
,
.
,
,
新知探究
例 2: 10年前, 母亲的年龄是儿子的6倍; 10年后, 母亲的年龄是儿子的2倍.
求母子现在的年龄?
解:设现在母亲的年龄为 x岁, 儿子的年龄为 y岁. 根据题意得
答: 现在母亲的年龄为40岁, 儿子的年龄为15岁.
,
,
,
.
新知探究
例3:某市举办中学生足球比赛, 规定胜一场得3分, 平一场得1分. 市第二中学足球队比赛11场, 没有输过一场, 共得27分, 试问该队胜几场, 平几场?
分析:题中的未知量有胜的场数和平的场数, 等量关系有胜的场数+平的场数=11; 胜场得分+平场得分=27.
胜场 平场 合计
场数
得分
x
3x
y
y
11
27
解:设市第二中学足球队胜 x场, 平 y场. 依题意可得
8
y
3x
y
3
答:该市第二中学足球队胜8场, 平3场.
x
通过上述两题, 总结
用二元一次方程组解
决实际问题的步骤.
知识归纳
列方程组解应用题的关键在于审题, 弄清题意及题中的相等关系.
新知探究
列:分析题意, 找出两个等量关系, 列出方程组.
用方程组解决实际问题的步骤:
审:弄清题目中的数量关系, 设出两个未知数.
解:解方程组, 求出未知数的值.
验:检验求得的值是否正确和符合实际情形.
答:写出答案.
新知探究
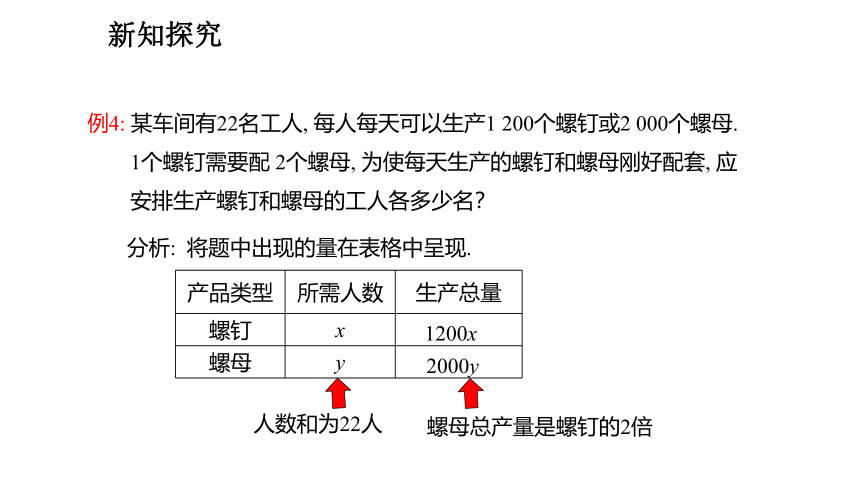
例4: 某车间有22名工人, 每人每天可以生产1 200个螺钉或2 000个螺母.
1个螺钉需要配 2个螺母, 为使每天生产的螺钉和螺母刚好配套, 应
安排生产螺钉和螺母的工人各多少名?
分析: 将题中出现的量在表格中呈现.
产品类型 所需人数 生产总量
螺钉 x
螺母 y
螺母总产量是螺钉的2倍
人数和为22人
1200x
2000y
新知探究
解:设生产螺钉的 x人, 生产螺母的 y人.
依题意, 可列方程组
解方程组, 得
答:设生产螺钉的10人, 生产螺母的12人.
解决配套问题要弄清:
(1)每套产品中各部分的比例;
(2)生产各部分的工人数之和=工人总数.
x
新知探究
例5:某高校共有5个大餐厅和2个小餐厅, 经过测试: 同时开放1个大餐厅和
2个小餐厅, 可供1680名学生就餐; 同时开放2个大餐厅和1个小餐厅,
可供2280名学生就餐. (1)求1个大餐厅和1个小餐厅分别可供多少名学生就餐? (2)若7个餐厅同时开放, 请估计一下能否供应全校的5300名学生就餐,
并说明理由.
新知探究
解: (1)设1个大餐厅和1个小餐厅分别可供 x名, y名学生就餐.
x+2y=1680,
2x+y=2280,
解得
x=960,
y=360.
(2)若7个餐厅同时开放, 则有
5×960+2×360=5320,
答: 若7个餐厅同时开放, 可以供应全校的5300名学生就餐.
5320 > 5300.
依题意得
答: 1个大餐厅和1个小餐厅分别可供960名, 360名学生就餐.
实际问题
数学问题的解
(二元一次方程组的解)
问题答案
数学问题
(二元一次方程组)
设未知数, 列方程组
转化
解方程组
消元
检验
知识归纳
课堂小结
用二元一次方程组解决实际问题
列方程组解应用题的关键在于审题, 弄清题意及题中的相等关系.
用方程组解决实际问题的步骤.
课堂小测
1.一个两位数的十位数字与个位数字的和是8, 把这个两位数加上18,结果恰好成为数字对调后组成的两位数, 求原两位数. 设原两位数的个位数字为x, 十位数字为y, 所列方程组正确的是( )
B.
D.
B
,
,
,
,
课堂小测
3.学校文艺部组织部分文艺积极分子看演出, 共购得8张甲票,
4张乙票, 总共用了112元. 已知每张甲票比乙票贵2元,则甲票、
乙票的票价分别是 ( )
A.甲票10元/张, 乙票8元/张 B.甲票8元/张, 乙票10元/张
C.甲票12元/张, 乙票10元/张 D.甲票10元/张, 乙票12元/张
A
2.我国古代数学巨著《孙子算经》中的“鸡兔同笼”题为“今有
雉(鸡)兔同笼, 上有三十五头, 下有九十四足. 问雉兔各几何”.
正确答案是 ( )
A.鸡24只, 兔11只 B.鸡23只, 兔12只
C.鸡11只, 兔24只 D.鸡12只, 兔23只
B
课堂小测
4.大数和小数的差为12, 这两个数的和为60, 则
大数是______, 小数是____.
5.买14支铅笔和6本练习本, 共用5.4元. 若铅每
支 x元, 练习本每本 y元, 写出以和为未知数的
方程为___________.
36
24
14x+6y=5.4
课堂小测
6.用白铁皮做水桶,每张铁皮能做1个桶身或8个桶底, 而1个桶身1个
桶底正好配套做1个水桶, 现在有63张这样的铁皮, 则需要用多少张
做桶身, 多少张做桶底正好配套
解:设用 x张铁皮做桶身, y张铁皮做桶底.
根据题意得
解得
答: 需要用56张铁皮做桶身, 7张铁皮做桶底正好配套.
课堂小测
7.在读书活动中, 某校将一批书按以下原则分给各班: 第一班取走100本, 又取走余下的十分之一: 第二班取走200本, 又取走余下的十分之一 ... 以此类推, 最后全部书被各班取走, 而且各班所得的书相等, 问共多少本书, 班数是多少
解得
x=8100,
y=900.
答: 共有8100本书, 9个班级.
y
8.通过对一份中学生营养快餐的检测, 得到以下信息:
①快餐总质量为300g;
②快餐的成分: 蛋白质、碳水化合物、脂肪、矿物质;
③蛋白质和脂肪含量占50%; 矿物质的含量是脂肪含量的2倍; 蛋白质和碳水化合物含量占85%.
根据上述数据回答下面的问题:
⑴分别求出营养快餐中蛋白质、碳水化合物、脂肪、矿物质的质量和所占百分比;
⑵根据计算结果制作扇形统计图表示营养快餐成分的信息.
课堂小测
解:(1)设一份营养快餐中的蛋白质 x g, 脂肪 y g. 根据题意,
得
x+y=300×50%,
(300×85%-x)+2y=300×50%.
解这个方程组, 得
x=135, y=15.
经检验, 符合题意.
∴ 2y=2×15=30 (g),
300×85%-x=255-135=120 (g)
课堂小测
根据以上计算, 可得下面的统计表.
蛋白质
脂肪
矿物质
碳水化合物
合计
各种成分的质量(g)
135
15
30
120
300
各种成分所占百分比
45%
5%
10%
40%
100%
课堂小测
(2)所求扇形统计图如图.
中学生营养快餐成分扇形统计图
10%
5%
45%
40%
课堂小测
七年级数学人教版·下册
8.3.1 用二元一次方程组解决数字,
和、差、倍、分等问题
授课人:XXXX
第八章
二元一次方程组
教学目标
1.以方程组为工具, 分析、解决含有多个未知数的实际问题;(重点)
2.确定解题策略, 二元一次方程组解决数字, 和、差、倍、分等问题.
(难点)
新课导入
-3
-1
2
新知探究
例1:一个两位数, 十位上的数字比个位上的数字大5, 如果把十位上的数
字与个位上的数字交换位置, 那么得到的新两位数比原来的两位数
的一半还少9, 求这个两位数?
解:设个位上的数字为 x, 十位上的数字为 y. 根据题意得
答:这个两位数是72.
.
,
.
,
,
新知探究
例 2: 10年前, 母亲的年龄是儿子的6倍; 10年后, 母亲的年龄是儿子的2倍.
求母子现在的年龄?
解:设现在母亲的年龄为 x岁, 儿子的年龄为 y岁. 根据题意得
答: 现在母亲的年龄为40岁, 儿子的年龄为15岁.
,
,
,
.
新知探究
例3:某市举办中学生足球比赛, 规定胜一场得3分, 平一场得1分. 市第二中学足球队比赛11场, 没有输过一场, 共得27分, 试问该队胜几场, 平几场?
分析:题中的未知量有胜的场数和平的场数, 等量关系有胜的场数+平的场数=11; 胜场得分+平场得分=27.
胜场 平场 合计
场数
得分
x
3x
y
y
11
27
解:设市第二中学足球队胜 x场, 平 y场. 依题意可得
8
y
3x
y
3
答:该市第二中学足球队胜8场, 平3场.
x
通过上述两题, 总结
用二元一次方程组解
决实际问题的步骤.
知识归纳
列方程组解应用题的关键在于审题, 弄清题意及题中的相等关系.
新知探究
列:分析题意, 找出两个等量关系, 列出方程组.
用方程组解决实际问题的步骤:
审:弄清题目中的数量关系, 设出两个未知数.
解:解方程组, 求出未知数的值.
验:检验求得的值是否正确和符合实际情形.
答:写出答案.
新知探究
例4: 某车间有22名工人, 每人每天可以生产1 200个螺钉或2 000个螺母.
1个螺钉需要配 2个螺母, 为使每天生产的螺钉和螺母刚好配套, 应
安排生产螺钉和螺母的工人各多少名?
分析: 将题中出现的量在表格中呈现.
产品类型 所需人数 生产总量
螺钉 x
螺母 y
螺母总产量是螺钉的2倍
人数和为22人
1200x
2000y
新知探究
解:设生产螺钉的 x人, 生产螺母的 y人.
依题意, 可列方程组
解方程组, 得
答:设生产螺钉的10人, 生产螺母的12人.
解决配套问题要弄清:
(1)每套产品中各部分的比例;
(2)生产各部分的工人数之和=工人总数.
x
新知探究
例5:某高校共有5个大餐厅和2个小餐厅, 经过测试: 同时开放1个大餐厅和
2个小餐厅, 可供1680名学生就餐; 同时开放2个大餐厅和1个小餐厅,
可供2280名学生就餐. (1)求1个大餐厅和1个小餐厅分别可供多少名学生就餐? (2)若7个餐厅同时开放, 请估计一下能否供应全校的5300名学生就餐,
并说明理由.
新知探究
解: (1)设1个大餐厅和1个小餐厅分别可供 x名, y名学生就餐.
x+2y=1680,
2x+y=2280,
解得
x=960,
y=360.
(2)若7个餐厅同时开放, 则有
5×960+2×360=5320,
答: 若7个餐厅同时开放, 可以供应全校的5300名学生就餐.
5320 > 5300.
依题意得
答: 1个大餐厅和1个小餐厅分别可供960名, 360名学生就餐.
实际问题
数学问题的解
(二元一次方程组的解)
问题答案
数学问题
(二元一次方程组)
设未知数, 列方程组
转化
解方程组
消元
检验
知识归纳
课堂小结
用二元一次方程组解决实际问题
列方程组解应用题的关键在于审题, 弄清题意及题中的相等关系.
用方程组解决实际问题的步骤.
课堂小测
1.一个两位数的十位数字与个位数字的和是8, 把这个两位数加上18,结果恰好成为数字对调后组成的两位数, 求原两位数. 设原两位数的个位数字为x, 十位数字为y, 所列方程组正确的是( )
B.
D.
B
,
,
,
,
课堂小测
3.学校文艺部组织部分文艺积极分子看演出, 共购得8张甲票,
4张乙票, 总共用了112元. 已知每张甲票比乙票贵2元,则甲票、
乙票的票价分别是 ( )
A.甲票10元/张, 乙票8元/张 B.甲票8元/张, 乙票10元/张
C.甲票12元/张, 乙票10元/张 D.甲票10元/张, 乙票12元/张
A
2.我国古代数学巨著《孙子算经》中的“鸡兔同笼”题为“今有
雉(鸡)兔同笼, 上有三十五头, 下有九十四足. 问雉兔各几何”.
正确答案是 ( )
A.鸡24只, 兔11只 B.鸡23只, 兔12只
C.鸡11只, 兔24只 D.鸡12只, 兔23只
B
课堂小测
4.大数和小数的差为12, 这两个数的和为60, 则
大数是______, 小数是____.
5.买14支铅笔和6本练习本, 共用5.4元. 若铅每
支 x元, 练习本每本 y元, 写出以和为未知数的
方程为___________.
36
24
14x+6y=5.4
课堂小测
6.用白铁皮做水桶,每张铁皮能做1个桶身或8个桶底, 而1个桶身1个
桶底正好配套做1个水桶, 现在有63张这样的铁皮, 则需要用多少张
做桶身, 多少张做桶底正好配套
解:设用 x张铁皮做桶身, y张铁皮做桶底.
根据题意得
解得
答: 需要用56张铁皮做桶身, 7张铁皮做桶底正好配套.
课堂小测
7.在读书活动中, 某校将一批书按以下原则分给各班: 第一班取走100本, 又取走余下的十分之一: 第二班取走200本, 又取走余下的十分之一 ... 以此类推, 最后全部书被各班取走, 而且各班所得的书相等, 问共多少本书, 班数是多少
解得
x=8100,
y=900.
答: 共有8100本书, 9个班级.
y
8.通过对一份中学生营养快餐的检测, 得到以下信息:
①快餐总质量为300g;
②快餐的成分: 蛋白质、碳水化合物、脂肪、矿物质;
③蛋白质和脂肪含量占50%; 矿物质的含量是脂肪含量的2倍; 蛋白质和碳水化合物含量占85%.
根据上述数据回答下面的问题:
⑴分别求出营养快餐中蛋白质、碳水化合物、脂肪、矿物质的质量和所占百分比;
⑵根据计算结果制作扇形统计图表示营养快餐成分的信息.
课堂小测
解:(1)设一份营养快餐中的蛋白质 x g, 脂肪 y g. 根据题意,
得
x+y=300×50%,
(300×85%-x)+2y=300×50%.
解这个方程组, 得
x=135, y=15.
经检验, 符合题意.
∴ 2y=2×15=30 (g),
300×85%-x=255-135=120 (g)
课堂小测
根据以上计算, 可得下面的统计表.
蛋白质
脂肪
矿物质
碳水化合物
合计
各种成分的质量(g)
135
15
30
120
300
各种成分所占百分比
45%
5%
10%
40%
100%
课堂小测
(2)所求扇形统计图如图.
中学生营养快餐成分扇形统计图
10%
5%
45%
40%
课堂小测
