2021-2022学年度人教版七年级数学下册 8.3.3 用二元一次方程组解决增长率、利润等问题 课件(共16页)
文档属性
| 名称 | 2021-2022学年度人教版七年级数学下册 8.3.3 用二元一次方程组解决增长率、利润等问题 课件(共16页) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-30 00:00:00 | ||
图片预览






文档简介
(共16张PPT)
七年级数学人教版·下册
8.3.3 用二元一次方程组解决增长率、利润等问题
授课人:XXXX
第八章
二元一次方程组
教学目标
1. 分析题目中的各个量的关系;(重点)
2.用二元一次方程组解决增长率、利润问题.(难点)
新课导入
某班为奖励在运动会上取得较好成绩的运动员, 花了400元钱购买甲、乙两种奖品共30件, 其中甲种奖品每件16元, 乙种奖品每件12元, 求甲、乙两种奖品各买多少件?若设购买甲种奖品 x件, 乙种奖品 y件, 则方程组正确的是( )
B
C
D
例1:某市现有42万人口, 计划一年后城镇人口增加0.8%, 农村人口增加 1.1%,
这样全市人口将增加1%, 求这个市现在的城镇人口与农村人口?
分析: 两个相等关系1.现在城镇人口+ 农村人口=现在全市总人口
2.明年增加后的城镇人口+明年增加后的农村人口=明年全市总人口
解:这个市现在的城镇人口有x万人, 农村人口有y万人.
根据题意得
答: 这个市现在的城镇人口有14万人, 农村人口有28万人.
,
,
,
.
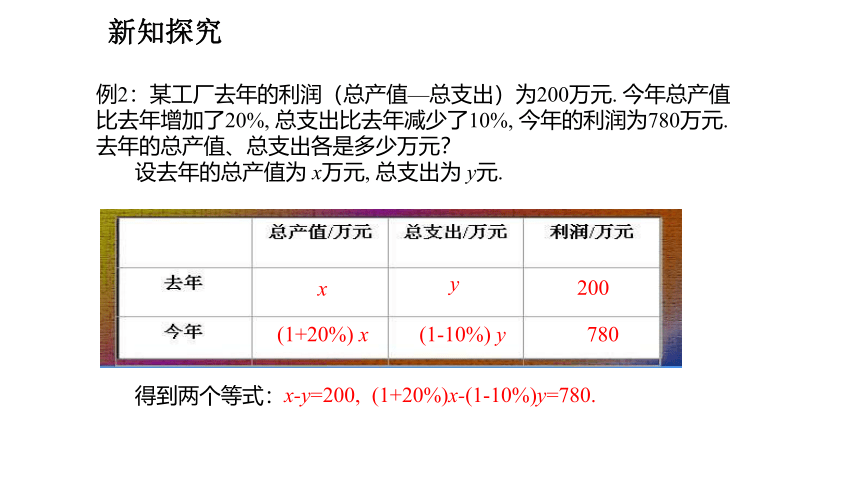
新知探究
得到两个等式:
设去年的总产值为 x万元, 总支出为 y元.
x
y
200
(1+20%) x
(1-10%) y
780
x-y=200,
(1+20%)x-(1-10%)y=780.
例2:某工厂去年的利润(总产值—总支出)为200万元. 今年总产值比去年增加了20%, 总支出比去年减少了10%, 今年的利润为780万元.去年的总产值、总支出各是多少万元?
新知探究
解:设去年的总产值为x万元, 总支出为y万元, 由题意得.
解这个方程组, 得
答:去年的总收入为2000万元,总支出为1800万元.
新知探究
.
,
,
,
知识归纳
用方程组解决问题时, 可以先设计表格, 通过填表对有关数量进行整理, 发现等量关系,列出方程组, 求出方程组的解后, 应进一步考虑它是否符合问题的实际意义.
新知探究
例3: 某商场按定价销售某种商品时, 每件可获利45元; 该商品按定价的八五折销售8件与将定价降低35元销售12件所获利润相等. 该商品的进价、定价分别是多少
解: 设该商品定价是 x 元, 进价 y 元.
根据题意可列出方程组
解方程组, 得
答: 该商品定价是200元, 进价155 元.
,
.
,
,
新知探究
例4: 某超市在 “五一” 期间寻顾客实行优惠, 规定如下:
(2)若顾客在该超市一次性购物 x元, 当小于500元但不小于200元时, 他实际付款 元; 当x大于或等于500元时, 他实际付款 元(用含 x 的代数式表示);
一次性购物 优惠方法
少于200元 不予优惠
低于500元但不低于200元 九折优惠
500元或大于500元 其中500元部分给予九折优惠, 超过500部分给予八折优惠
(1)王老师一次购物600元, 他实际付款 元 ;
530
0.9x
0.8x+50
新知探究
(3)如果王老师两次购物合计820元, 他实际付款共计728元,且第一次购物的货款少于第二次购物的, 求两次购物各多少元?
其中500元部分给予九折优惠, 超过500部分给予八折优惠
500元或等于500元
九折优惠
低于500元但不低于200元
不予优惠
少于200元
优惠方法
一次性购物
解: 设第一次购物的货款为 x元, 第二次购物的货款为 y元.
①当 x<200, y>500时, 由题意得
x+y=820,
x+0.8y+50=728,
解得
x=110,
y=710;
新知探究
②当 200≤ x<500, y ≥ 500时, 由题意得
x+y=820,
0.9x+0.8y+50=728,
解得
x=220,
y=600;
③当200≤ x<500, 200≤ y <500时,由题意得
综上所述, 两次购物的分别为110元、710元或220元、600元.
x+y=820,
0.9x+0.9y=728,
此方程组无解.
课堂小结
用二元一次方程组解决实际问题
方程组解决问题时, 可以先设计表格, 通过填表对有关数量进行整理, 发现等量关系, 列出方程组, 求出方程组的解后, 应进一步考虑它是否符合问题的实际意义.
列二元一次方程组的关键是寻找等量关系.找等量关系常用的方法: (1)直接列式法; (2)列表法; (3)图形示意法
课堂小测
1.有一个商店把某件商品按进价加20%作为定价, 可是总卖不出去;
后来老板按定价减20%以96元出售, 很快就卖掉了, 则这次生意盈
亏情况是 ( )
A.赚6元 B.不亏不赚 C.亏4元 D.亏24元
C
课堂小测
2.CNI公司去年的利润(总产值—总支出)为200万元. 今年总产值比去年增加了20%, 总支出比去年减少了10%, 今年的利润为780万元. 去年的总产值、总支出各是多少万元?
解: 设去年的总产值为 x万元, 总支出为 y万元, 则
今年的总产值=(1+20%)x万元,
今年的总支出=(1-10%)y万元.
由题意得
解得
答: 去年的总收入为2000万元, 总支出为1800万元.
3.某电器商场销售A, B两种型号计算器, 两种计算器的进货价格分别为每台30元, 40元, 商场销售5台A型号和1台B型号计算器, 可获利润76元; 销售6台A型号和3台B型号计算器, 可获利润120元. (1)求商场销售A, B两种型号计算器的销售价格分别是多少元?(利润=销售价格-进货价格); (2)商场准备用不多于2500元的资金购进A, B两种型号计算器共70台, 问最少需要购进A型号的计算器多少台?
课堂小测
(2)设购进A型计算器a台, 则购进B型计算器(70-a)台, 则30a+40(70-a) ≤ 2500,解得 a ≥ 30. 答: 最少需要购进A型号的计算器30台.
解:(1)设A种型号计算器的销售价格是x元, B种型号计算器的销售价格是 y元.
由题意得 解得
答: A种型号计算器的销售价格是42元, B种型号计算器的销售价格是56元.
,
,
,
.
七年级数学人教版·下册
8.3.3 用二元一次方程组解决增长率、利润等问题
授课人:XXXX
第八章
二元一次方程组
教学目标
1. 分析题目中的各个量的关系;(重点)
2.用二元一次方程组解决增长率、利润问题.(难点)
新课导入
某班为奖励在运动会上取得较好成绩的运动员, 花了400元钱购买甲、乙两种奖品共30件, 其中甲种奖品每件16元, 乙种奖品每件12元, 求甲、乙两种奖品各买多少件?若设购买甲种奖品 x件, 乙种奖品 y件, 则方程组正确的是( )
B
C
D
例1:某市现有42万人口, 计划一年后城镇人口增加0.8%, 农村人口增加 1.1%,
这样全市人口将增加1%, 求这个市现在的城镇人口与农村人口?
分析: 两个相等关系1.现在城镇人口+ 农村人口=现在全市总人口
2.明年增加后的城镇人口+明年增加后的农村人口=明年全市总人口
解:这个市现在的城镇人口有x万人, 农村人口有y万人.
根据题意得
答: 这个市现在的城镇人口有14万人, 农村人口有28万人.
,
,
,
.
新知探究
得到两个等式:
设去年的总产值为 x万元, 总支出为 y元.
x
y
200
(1+20%) x
(1-10%) y
780
x-y=200,
(1+20%)x-(1-10%)y=780.
例2:某工厂去年的利润(总产值—总支出)为200万元. 今年总产值比去年增加了20%, 总支出比去年减少了10%, 今年的利润为780万元.去年的总产值、总支出各是多少万元?
新知探究
解:设去年的总产值为x万元, 总支出为y万元, 由题意得.
解这个方程组, 得
答:去年的总收入为2000万元,总支出为1800万元.
新知探究
.
,
,
,
知识归纳
用方程组解决问题时, 可以先设计表格, 通过填表对有关数量进行整理, 发现等量关系,列出方程组, 求出方程组的解后, 应进一步考虑它是否符合问题的实际意义.
新知探究
例3: 某商场按定价销售某种商品时, 每件可获利45元; 该商品按定价的八五折销售8件与将定价降低35元销售12件所获利润相等. 该商品的进价、定价分别是多少
解: 设该商品定价是 x 元, 进价 y 元.
根据题意可列出方程组
解方程组, 得
答: 该商品定价是200元, 进价155 元.
,
.
,
,
新知探究
例4: 某超市在 “五一” 期间寻顾客实行优惠, 规定如下:
(2)若顾客在该超市一次性购物 x元, 当小于500元但不小于200元时, 他实际付款 元; 当x大于或等于500元时, 他实际付款 元(用含 x 的代数式表示);
一次性购物 优惠方法
少于200元 不予优惠
低于500元但不低于200元 九折优惠
500元或大于500元 其中500元部分给予九折优惠, 超过500部分给予八折优惠
(1)王老师一次购物600元, 他实际付款 元 ;
530
0.9x
0.8x+50
新知探究
(3)如果王老师两次购物合计820元, 他实际付款共计728元,且第一次购物的货款少于第二次购物的, 求两次购物各多少元?
其中500元部分给予九折优惠, 超过500部分给予八折优惠
500元或等于500元
九折优惠
低于500元但不低于200元
不予优惠
少于200元
优惠方法
一次性购物
解: 设第一次购物的货款为 x元, 第二次购物的货款为 y元.
①当 x<200, y>500时, 由题意得
x+y=820,
x+0.8y+50=728,
解得
x=110,
y=710;
新知探究
②当 200≤ x<500, y ≥ 500时, 由题意得
x+y=820,
0.9x+0.8y+50=728,
解得
x=220,
y=600;
③当200≤ x<500, 200≤ y <500时,由题意得
综上所述, 两次购物的分别为110元、710元或220元、600元.
x+y=820,
0.9x+0.9y=728,
此方程组无解.
课堂小结
用二元一次方程组解决实际问题
方程组解决问题时, 可以先设计表格, 通过填表对有关数量进行整理, 发现等量关系, 列出方程组, 求出方程组的解后, 应进一步考虑它是否符合问题的实际意义.
列二元一次方程组的关键是寻找等量关系.找等量关系常用的方法: (1)直接列式法; (2)列表法; (3)图形示意法
课堂小测
1.有一个商店把某件商品按进价加20%作为定价, 可是总卖不出去;
后来老板按定价减20%以96元出售, 很快就卖掉了, 则这次生意盈
亏情况是 ( )
A.赚6元 B.不亏不赚 C.亏4元 D.亏24元
C
课堂小测
2.CNI公司去年的利润(总产值—总支出)为200万元. 今年总产值比去年增加了20%, 总支出比去年减少了10%, 今年的利润为780万元. 去年的总产值、总支出各是多少万元?
解: 设去年的总产值为 x万元, 总支出为 y万元, 则
今年的总产值=(1+20%)x万元,
今年的总支出=(1-10%)y万元.
由题意得
解得
答: 去年的总收入为2000万元, 总支出为1800万元.
3.某电器商场销售A, B两种型号计算器, 两种计算器的进货价格分别为每台30元, 40元, 商场销售5台A型号和1台B型号计算器, 可获利润76元; 销售6台A型号和3台B型号计算器, 可获利润120元. (1)求商场销售A, B两种型号计算器的销售价格分别是多少元?(利润=销售价格-进货价格); (2)商场准备用不多于2500元的资金购进A, B两种型号计算器共70台, 问最少需要购进A型号的计算器多少台?
课堂小测
(2)设购进A型计算器a台, 则购进B型计算器(70-a)台, 则30a+40(70-a) ≤ 2500,解得 a ≥ 30. 答: 最少需要购进A型号的计算器30台.
解:(1)设A种型号计算器的销售价格是x元, B种型号计算器的销售价格是 y元.
由题意得 解得
答: A种型号计算器的销售价格是42元, B种型号计算器的销售价格是56元.
,
,
,
.
