2021-2022学年度人教版七年级数学下册 9.3 一元一次不等式组 课件(共23张)
文档属性
| 名称 | 2021-2022学年度人教版七年级数学下册 9.3 一元一次不等式组 课件(共23张) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-30 15:23:14 | ||
图片预览






文档简介
(共23张PPT)
七年级数学人教版·下册
9.3 一元一次不等式组
授课人:XXXX
第九章
不等式与不等式组
教学目标
1.求解一元一次不等式组, 求一元一次不等式组的特殊解;(重点)
2.对一元一次不等式组解集的理解.(难点)
新课导入
小强和爸爸、妈妈三人在操场上玩跷跷板, 爸爸的体重为72kg, 体重只有妈妈一半的小强和妈妈一同坐在跷跷板的另一端, 这时爸爸所在的一端仍然着地. 后来, 小强借来一副质量为6kg的哑铃, 加在他和妈妈坐的一端, 结果爸爸被跷起离地, 则小强的体重约是多少
在这个问题中, 如果设小强的体重为 x kg, 可以列出下列两个不等式:
2x+x < 72, 2x+x+6 > 72.
知识归纳
类似于方程组, 把两个不等式合起来, 可以组成一个一元一次不等式组.
新知探究
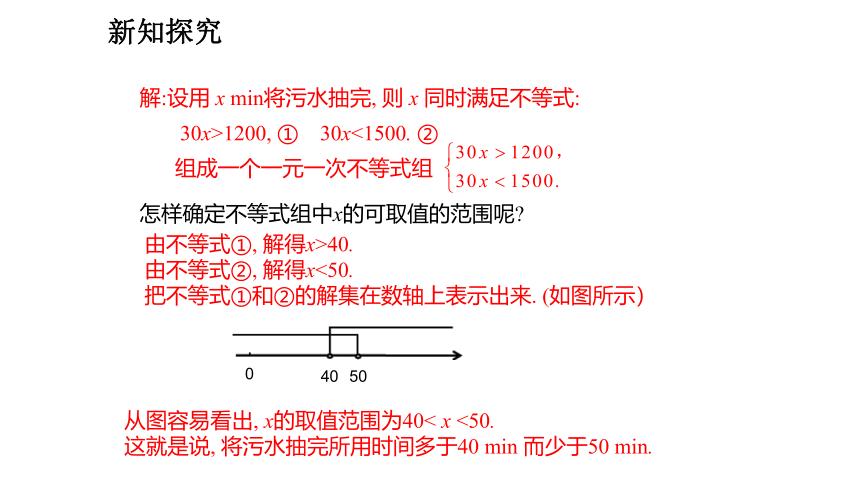
例1: 用每分可抽30 t 水的抽水机来抽污水管道里积存的污水, 估计积存的污水超过1200 t 而不足1500 t, 那么将污水抽完所用时间的范围是什么
思考:
(1)如果设 x min将污水抽完, 可以列哪两个不等式
(2)通过一个不等式, 能确定 x 的取值范围吗
(3)用什么办法能够确定 x 的取值范围
(4)确定的 x 的取值范围, 怎样在数轴上表示
新知探究
解:设用 x min将污水抽完, 则 x 同时满足不等式:
30x>1200, ① 30x<1500. ②
怎样确定不等式组中x的可取值的范围呢
由不等式①, 解得x>40.
由不等式②, 解得x<50.
把不等式①和②的解集在数轴上表示出来. (如图所示)
从图容易看出, x的取值范围为40< x <50.
这就是说, 将污水抽完所用时间多于40 min 而少于50 min.
组成一个一元一次不等式组
0
40
50
知识归纳
类比方程组的求解, 不等式组中的各个不等式解集的公共部分, 就是不等式组中的未知数的取值范围.
新知探究
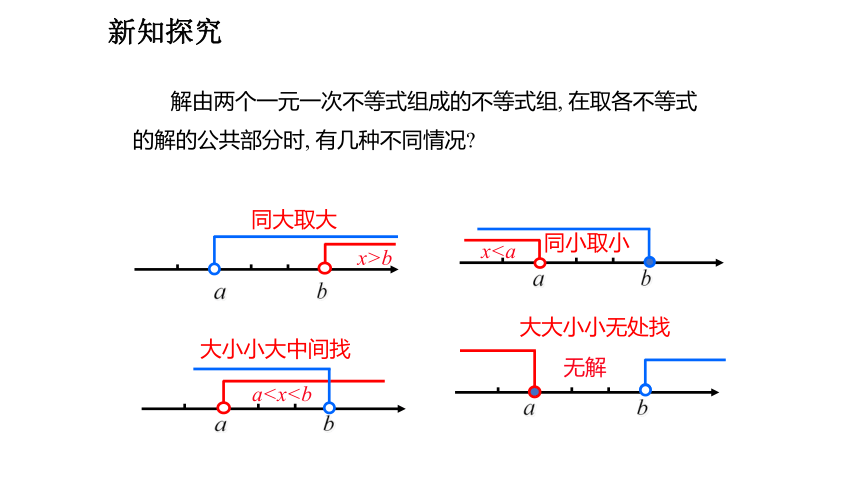
解由两个一元一次不等式组成的不等式组, 在取各不等式的解的公共部分时, 有几种不同情况
a b
a b
a b
a b
同大取大
同小取小
大小小大中间找
大大小小无处找
x>b
xa无解
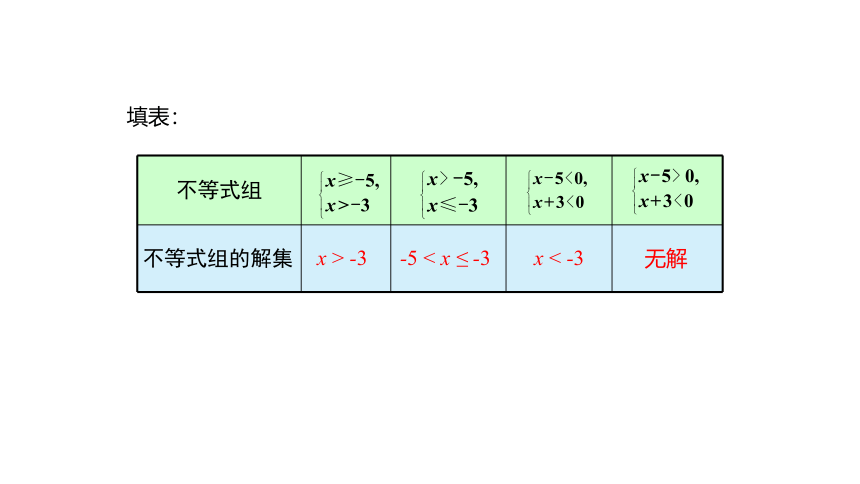
填表:
不等式组
不等式组的解集
x > -3
-5 < x ≤ -3
x < -3
无解
知识归纳
一般地, 把几个一元一次不等式解集的公共部分,
叫作由它们所组成的一元一次不等式组的解集.
求不等式组的解集的过程, 叫作解不等式组.
新知探究
例2: 解下列不等式组.
解:(1)解不等式①, 得 x > 2.
解不等式②, 得 x > 3.
把不等式①和②的解集在数轴上如图.
找出两个不等式解集的公共部分,
得不等式组的解集 x > 3.
(2)解不等式①, 得 x ≥ 8.
解不等式②, 得 x < .
把不等式①和②的解集在数轴上如图.
从上图可以看到这两个不等式的
解集没有公共部分, 不等式组无解.
新知探究
例3: x取哪些整数值时, 不等式5x+2>3(x-1)与 x- 1 ≤ 7- x 都成立
问题1: 5x+2>3(x- 1)的解集是什么
问题2: x- 1 ≤ 7- x 的解集是什么
问题3: 怎样才能使得 x 适合两个不等式
问题4: 适合两个不等式的整数 x 有哪些
新知探究
解析: 解决问题1和问题2就是解不等式求解集. 通过建立不等式组可
以求得两个不等式解集的公共部分. 求出这两个不等式组成的
不等式组的解集, 解集中的整数就是 x 可取的整数值.
新知探究
例4: 3个小组计划在10天内生产500件产品(每天生产量相同),
按原先的生产速度, 不能完成任务; 如果每个小组每天比
原先生产1件产品, 就能提前完成任务. 每个小组原先每天
生产多少件产品?
解: 设每个小组原先每天生产 x 件产品.
由题意, 得
3×10x < 500,
3×10(x+1) > 500,
解不等式组, 得 ,
根据题意, x 的值应是整数, 所以 x=16.
答: 每个小组原先每天生产16件产品.
课堂小结
一元一次不等式组
类似于方程组, 把这两个不等式合起来, 组成一个一元一次不等式组.
一般地, 把几个一元一次不等式解集的公共部分, 叫作由它们所组成的一元一次不等式组的解集.
求不等式组的解集的过程, 叫作解不等式组.
课堂小测
1.已知点P(3- m, m- 1)在第二象限, 则m的取值范围在数轴上表示正确的是
( )
A B C D
A. B. C. D.
2.不等式组的解集在数轴上表示如图所示, 则该不等式组可能为 ( )
A
B
课堂小测
a ≤ -1
-3 < a ≤ -2
课堂小测
课堂小测
课堂小测
7.把一篮苹果分给几个学生, 若每人分4个, 则剩余3个; 若每人分6个, 则最后一个学生最多分2个, 求学生人数和苹果分别是多少?
解: 设学生有 x 个, 则苹果有(4x+3)个.
根据题意,得
(4x+3)-6(x-1) > 0,
(4x+3)-6(x-1) ≤ 2.
解不等式组, 得3.5 < x < 4.5
根据题意, x的值应是整数, 所以 x=4, 则4x+3=19.
答: 学生有4人, 苹果有19个.
课堂小测
8.某中学为提升学生的课外阅读能力, 拓展学生的知识面, 决心打造 “书香校园”,计划用不超过1900本科技类书籍和1620本人文类书籍, 组建中、小型两类图书角共30个. 已知组建一个中型图书角需科技类书籍80本, 人文类书籍50本; 组建一个小型图书角需科技类书籍30本, 人文类书籍60本.
(1)符合题意的组建方案有几种 请你帮助学校设计出来;
解:(1)设组建中型图书角 x 个, 则组建小型图书角(30-x)个.
根据题意,得
解得18 ≤ x ≤ 20, 因为 x 是正整数, 所以 x 可取18,19, 20.
所以一共有三种组建方案:
方案一: 中型图书角建18个, 小型图书角建12个;
方案二: 中型图书角建19个, 小型图书角建11个;
方案三: 中型图书角建20个, 小型图书角建10个.
课堂小测
(2)若组建一个中型图书角的费用是860元, 组建一个小型图书角的费用是570元, 试说明(1)中哪种方案费用最低, 最低费用是多少元
(2)由(1)知方案一的费用:
18×860+12×570=22320(元);
方案二的费用: 19×860+11×570=22610(元);
方案三的费用: 20×860+10×570=22900(元).
所以方案一的费用最低, 最低费用是22320元.
七年级数学人教版·下册
9.3 一元一次不等式组
授课人:XXXX
第九章
不等式与不等式组
教学目标
1.求解一元一次不等式组, 求一元一次不等式组的特殊解;(重点)
2.对一元一次不等式组解集的理解.(难点)
新课导入
小强和爸爸、妈妈三人在操场上玩跷跷板, 爸爸的体重为72kg, 体重只有妈妈一半的小强和妈妈一同坐在跷跷板的另一端, 这时爸爸所在的一端仍然着地. 后来, 小强借来一副质量为6kg的哑铃, 加在他和妈妈坐的一端, 结果爸爸被跷起离地, 则小强的体重约是多少
在这个问题中, 如果设小强的体重为 x kg, 可以列出下列两个不等式:
2x+x < 72, 2x+x+6 > 72.
知识归纳
类似于方程组, 把两个不等式合起来, 可以组成一个一元一次不等式组.
新知探究
例1: 用每分可抽30 t 水的抽水机来抽污水管道里积存的污水, 估计积存的污水超过1200 t 而不足1500 t, 那么将污水抽完所用时间的范围是什么
思考:
(1)如果设 x min将污水抽完, 可以列哪两个不等式
(2)通过一个不等式, 能确定 x 的取值范围吗
(3)用什么办法能够确定 x 的取值范围
(4)确定的 x 的取值范围, 怎样在数轴上表示
新知探究
解:设用 x min将污水抽完, 则 x 同时满足不等式:
30x>1200, ① 30x<1500. ②
怎样确定不等式组中x的可取值的范围呢
由不等式①, 解得x>40.
由不等式②, 解得x<50.
把不等式①和②的解集在数轴上表示出来. (如图所示)
从图容易看出, x的取值范围为40< x <50.
这就是说, 将污水抽完所用时间多于40 min 而少于50 min.
组成一个一元一次不等式组
0
40
50
知识归纳
类比方程组的求解, 不等式组中的各个不等式解集的公共部分, 就是不等式组中的未知数的取值范围.
新知探究
解由两个一元一次不等式组成的不等式组, 在取各不等式的解的公共部分时, 有几种不同情况
a b
a b
a b
a b
同大取大
同小取小
大小小大中间找
大大小小无处找
x>b
x
填表:
不等式组
不等式组的解集
x > -3
-5 < x ≤ -3
x < -3
无解
知识归纳
一般地, 把几个一元一次不等式解集的公共部分,
叫作由它们所组成的一元一次不等式组的解集.
求不等式组的解集的过程, 叫作解不等式组.
新知探究
例2: 解下列不等式组.
解:(1)解不等式①, 得 x > 2.
解不等式②, 得 x > 3.
把不等式①和②的解集在数轴上如图.
找出两个不等式解集的公共部分,
得不等式组的解集 x > 3.
(2)解不等式①, 得 x ≥ 8.
解不等式②, 得 x < .
把不等式①和②的解集在数轴上如图.
从上图可以看到这两个不等式的
解集没有公共部分, 不等式组无解.
新知探究
例3: x取哪些整数值时, 不等式5x+2>3(x-1)与 x- 1 ≤ 7- x 都成立
问题1: 5x+2>3(x- 1)的解集是什么
问题2: x- 1 ≤ 7- x 的解集是什么
问题3: 怎样才能使得 x 适合两个不等式
问题4: 适合两个不等式的整数 x 有哪些
新知探究
解析: 解决问题1和问题2就是解不等式求解集. 通过建立不等式组可
以求得两个不等式解集的公共部分. 求出这两个不等式组成的
不等式组的解集, 解集中的整数就是 x 可取的整数值.
新知探究
例4: 3个小组计划在10天内生产500件产品(每天生产量相同),
按原先的生产速度, 不能完成任务; 如果每个小组每天比
原先生产1件产品, 就能提前完成任务. 每个小组原先每天
生产多少件产品?
解: 设每个小组原先每天生产 x 件产品.
由题意, 得
3×10x < 500,
3×10(x+1) > 500,
解不等式组, 得 ,
根据题意, x 的值应是整数, 所以 x=16.
答: 每个小组原先每天生产16件产品.
课堂小结
一元一次不等式组
类似于方程组, 把这两个不等式合起来, 组成一个一元一次不等式组.
一般地, 把几个一元一次不等式解集的公共部分, 叫作由它们所组成的一元一次不等式组的解集.
求不等式组的解集的过程, 叫作解不等式组.
课堂小测
1.已知点P(3- m, m- 1)在第二象限, 则m的取值范围在数轴上表示正确的是
( )
A B C D
A. B. C. D.
2.不等式组的解集在数轴上表示如图所示, 则该不等式组可能为 ( )
A
B
课堂小测
a ≤ -1
-3 < a ≤ -2
课堂小测
课堂小测
课堂小测
7.把一篮苹果分给几个学生, 若每人分4个, 则剩余3个; 若每人分6个, 则最后一个学生最多分2个, 求学生人数和苹果分别是多少?
解: 设学生有 x 个, 则苹果有(4x+3)个.
根据题意,得
(4x+3)-6(x-1) > 0,
(4x+3)-6(x-1) ≤ 2.
解不等式组, 得3.5 < x < 4.5
根据题意, x的值应是整数, 所以 x=4, 则4x+3=19.
答: 学生有4人, 苹果有19个.
课堂小测
8.某中学为提升学生的课外阅读能力, 拓展学生的知识面, 决心打造 “书香校园”,计划用不超过1900本科技类书籍和1620本人文类书籍, 组建中、小型两类图书角共30个. 已知组建一个中型图书角需科技类书籍80本, 人文类书籍50本; 组建一个小型图书角需科技类书籍30本, 人文类书籍60本.
(1)符合题意的组建方案有几种 请你帮助学校设计出来;
解:(1)设组建中型图书角 x 个, 则组建小型图书角(30-x)个.
根据题意,得
解得18 ≤ x ≤ 20, 因为 x 是正整数, 所以 x 可取18,19, 20.
所以一共有三种组建方案:
方案一: 中型图书角建18个, 小型图书角建12个;
方案二: 中型图书角建19个, 小型图书角建11个;
方案三: 中型图书角建20个, 小型图书角建10个.
课堂小测
(2)若组建一个中型图书角的费用是860元, 组建一个小型图书角的费用是570元, 试说明(1)中哪种方案费用最低, 最低费用是多少元
(2)由(1)知方案一的费用:
18×860+12×570=22320(元);
方案二的费用: 19×860+11×570=22610(元);
方案三的费用: 20×860+10×570=22900(元).
所以方案一的费用最低, 最低费用是22320元.
