人教版六年级下学期数学鸽巢问题(例1)课件(共24张PPT)
文档属性
| 名称 | 人教版六年级下学期数学鸽巢问题(例1)课件(共24张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 5.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-29 06:04:34 | ||
图片预览







文档简介
(共24张PPT)
六年级数学下册
数学广角
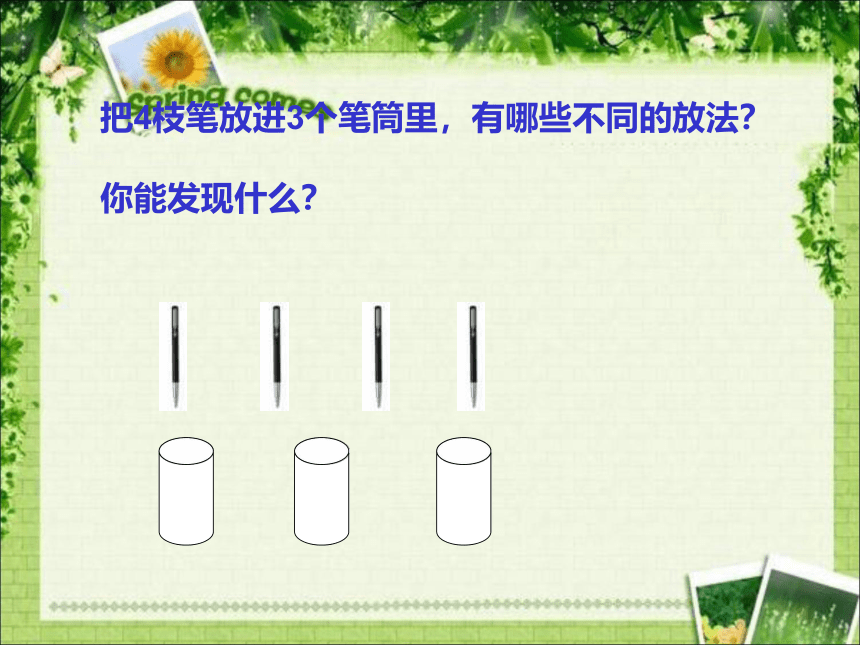
把4枝笔放进3个笔筒里,有哪些不同的放法?
你能发现什么?
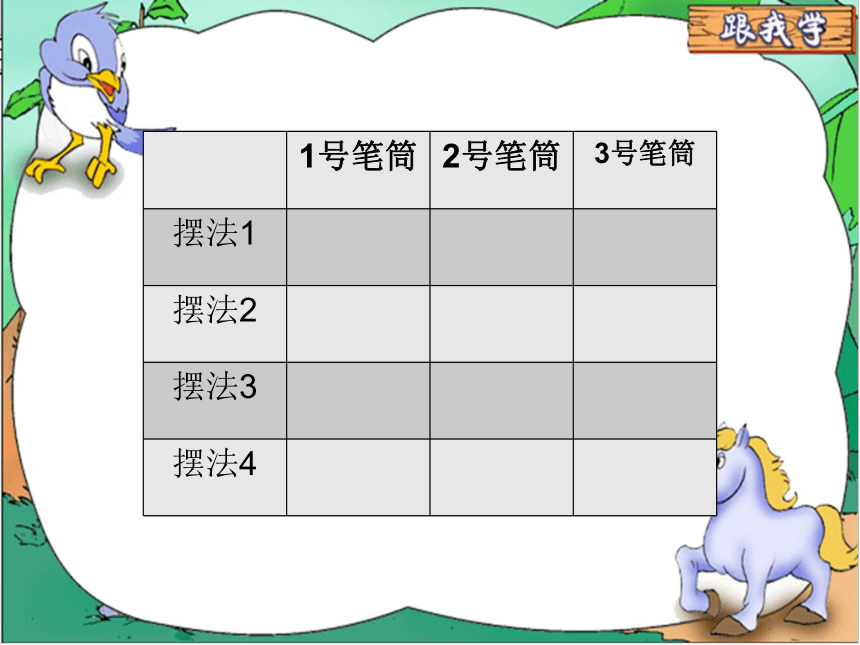
1号笔筒 2号笔筒 3号笔筒
摆法1
摆法2
摆法3
摆法4
活动任务:
将4枝笔放进3个文具盒里。
解决问题:
无论怎样放,总有一个文具盒里至少有( )枝笔。
小组合作:拿出4枝笔和3个文具盒,把这4枝笔放进这3个文具盒中摆一摆,放一放,看有几种情况?
至少放进2枝
实际操作
把4枝笔放进3个笔筒里,不管怎么放,总有一个笔筒里至少放进2枝笔,
这是为什么?
我们可以这样考虑:
如果我们先让每个笔筒里放1枝笔,最多放3枝。
剩下的1枝还要放进其中的一个笔筒。所以不管
怎么放,总有一个笔筒里至少放进2枝笔。
1.认识“鸽巢问题”
像上面的这个问题就是“鸽巢问题”,在这里“4支铅笔”就是“4个要分别放的物体”,“3个笔筒”就是“3个鸽巢”。把此问题用“鸽巢问题”的语言描述就是:把4个物体放进3个鸽巢,总有一个鸽巢里至少有2个物体。
最先发现这些规律的人是谁呢?他就是19世纪德国数学家“狄里克雷”,后人为了纪念他从这么平凡的事情中发现的规律,就把这个规律用他的名字命名,叫“狄里克雷原理”,又把它叫做“鸽巢原理”,还把它叫做 “抽屉原理”。
把4枝笔放进3个笔筒里,不管怎么放,总有一个笔筒里至少放进2枝笔,
那把5枝笔放进4个笔筒里呢?6枝笔5个笔筒呢?------
小组交流交流,发现了什么规律?
只要待分物体比容器数量多1,
用:待分物体÷容器数=1……1
多的这个无论放入哪个容器里,总有一个容器里至少放进2个物体。
你知道了吗?
一副扑克牌54张,去掉2个王。扑克牌中有红心、方块、梅花、黑桃4个花色。
抽取5张牌花色会怎样?
5张牌中至少有2张牌花色是相同的。
你知道这个游戏中
蕴含的道理吗?
抽牌
游戏
把5本书放进2个抽屉中,不管怎么放,总有一个抽屉至少放进几本书?
5本书平均放进2个抽屉中,每个抽屉放进2本,最多放了4本,剩下的一本不管怎么放,都能确保总有一个抽屉至少放进3本书。
通过今天的
学习你有什么收获?
请多指教!
六年级数学下册
数学广角
把4枝笔放进3个笔筒里,有哪些不同的放法?
你能发现什么?
1号笔筒 2号笔筒 3号笔筒
摆法1
摆法2
摆法3
摆法4
活动任务:
将4枝笔放进3个文具盒里。
解决问题:
无论怎样放,总有一个文具盒里至少有( )枝笔。
小组合作:拿出4枝笔和3个文具盒,把这4枝笔放进这3个文具盒中摆一摆,放一放,看有几种情况?
至少放进2枝
实际操作
把4枝笔放进3个笔筒里,不管怎么放,总有一个笔筒里至少放进2枝笔,
这是为什么?
我们可以这样考虑:
如果我们先让每个笔筒里放1枝笔,最多放3枝。
剩下的1枝还要放进其中的一个笔筒。所以不管
怎么放,总有一个笔筒里至少放进2枝笔。
1.认识“鸽巢问题”
像上面的这个问题就是“鸽巢问题”,在这里“4支铅笔”就是“4个要分别放的物体”,“3个笔筒”就是“3个鸽巢”。把此问题用“鸽巢问题”的语言描述就是:把4个物体放进3个鸽巢,总有一个鸽巢里至少有2个物体。
最先发现这些规律的人是谁呢?他就是19世纪德国数学家“狄里克雷”,后人为了纪念他从这么平凡的事情中发现的规律,就把这个规律用他的名字命名,叫“狄里克雷原理”,又把它叫做“鸽巢原理”,还把它叫做 “抽屉原理”。
把4枝笔放进3个笔筒里,不管怎么放,总有一个笔筒里至少放进2枝笔,
那把5枝笔放进4个笔筒里呢?6枝笔5个笔筒呢?------
小组交流交流,发现了什么规律?
只要待分物体比容器数量多1,
用:待分物体÷容器数=1……1
多的这个无论放入哪个容器里,总有一个容器里至少放进2个物体。
你知道了吗?
一副扑克牌54张,去掉2个王。扑克牌中有红心、方块、梅花、黑桃4个花色。
抽取5张牌花色会怎样?
5张牌中至少有2张牌花色是相同的。
你知道这个游戏中
蕴含的道理吗?
抽牌
游戏
把5本书放进2个抽屉中,不管怎么放,总有一个抽屉至少放进几本书?
5本书平均放进2个抽屉中,每个抽屉放进2本,最多放了4本,剩下的一本不管怎么放,都能确保总有一个抽屉至少放进3本书。
通过今天的
学习你有什么收获?
请多指教!
