人教版六年级下学期数学《正比例》课件(共27张PPT)
文档属性
| 名称 | 人教版六年级下学期数学《正比例》课件(共27张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 14.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-29 06:06:47 | ||
图片预览







文档简介
(共27张PPT)
正比例
人教版 六年级下册第四单元第四课时
问题导入、课前热身
我们还学过哪些数量关系式?试着说一说…
已知路程和时间,怎样求速度?
速度 = 路程÷时间
已知总价和数量,怎样求单价?
单价 = 总价÷数量
已知工作总量和工作时间,怎样求工作效率?
工作效率 =工作总量÷工作时间
小红在购物,购物的时候你能想起哪个数量关系式?它们的关系还有哪种说法?进入到我们今天的学习,来看教材。
自主学习、新知引入
请仔细阅读课本第45页例1的内容,回答里面的问题。
自主学习、精读教材
数量/m 1 2 3 4 5 6 7 8 …
总价/元 3.5 7 10.5 14 17.5 21 24.5 28 …
文具店有一种彩带,销售的数量与总价的关系如下表。
观察表格中的信息,回答这三个问题。
你能知道哪些信息?
就是总价和数量是有关系的两个量。
数量/m 1 2 3 4 5 6 7 8 …
总价/元 3.5 7 10.5 14 17.5 21 24.5 28 …
(1)表中有哪两种量
数量和总价
总价和数量是两种相关联的量
数量增加,总价随着增加。
数量减少,总价随着减少。
(2)总价是怎样随着数量的变化而变化的?
合作探究、初步感知
(3)相应的总价与数量的比分别是多少?比值是多少?
数量/m 1 2 3 4 5 6 7 8 …
总价/元 3.5 7 10.5 14 17.5 21 24.5 28 …
3.5
3.5
3.5
3.5
3.5
3.5
3.5
3.5
…
=
=
=
=
=
=
=
=
比值是3.5,实际就是彩带的单价。用式子表示为:
数量
总价
=
单价
相对应的总价和数量的比的比值是一定的。
单价是固定不变的量,也就是单价一定。
合作探究、明辨释疑
小组讨论:两种量成正比例关系要满足什么条件?
合作探究、明辨释疑
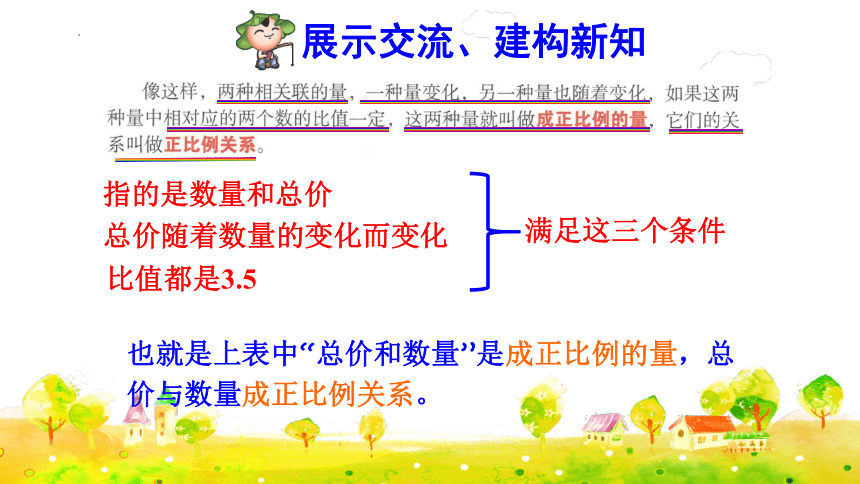
指的是数量和总价
总价随着数量的变化而变化
比值都是3.5
满足这三个条件
也就是上表中“总价和数量”是成正比例的量,总价与数量成正比例关系。
展示交流、建构新知
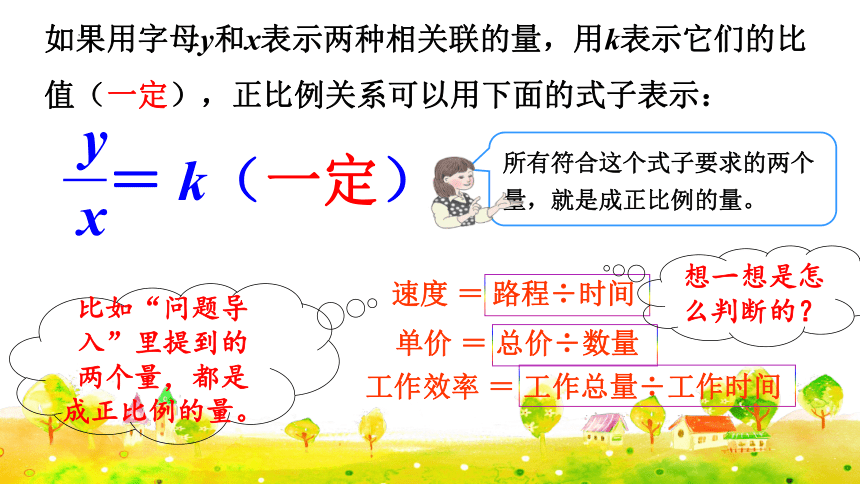
x
y
= k(一定)
所有符合这个式子要求的两个量,就是成正比例的量。
比如“问题导入”里提到的两个量,都是成正比例的量。
速度 = 路程÷时间
单价 = 总价÷数量
工作效率 = 工作总量÷工作时间
想一想是怎么判断的?
如果用字母y和x表示两种相关联的量,用k表示它们的比值(一定),正比例关系可以用下面的式子表示:
本题表中的数据还可以用图象表示:
数量/m 1 2 3 4 5 6 7 8 …
总价/元 3.5 7 10.5 14 17.5 21 24.5 28 …
你会观察这个图象了吗?试着根据这个图象回答下面的问题:
(1)从图中你发现了什么
答:这个图象是一条逐渐上升的直的线。
层层深入、感知图像
答:这两个点也在这条射线上,并且射线又在上升,它们的单价相等。
(2)把数对(10,35)和(12,42)所在的点描出来,并和上面的图象连起来并延长,你还能发现什么
(3)不计算,根据图象判断,如果买9 m彩带,总价是多少?49元能买多少米彩带
答:通过观察,我发现买9 m彩带总价是31.5元,49元能买14 m彩带。
31.5
31.5
(4)小明买的彩带的米数是小丽的2倍,他花的钱是小丽的几倍?
答:因为彩带的数量成倍地增加,总价也会成倍地增加,所以他花的钱是小丽的2倍。
彩带的单价一定
这样的例子还有很多,想一想你学过的数量关系式和计算公式,说说成正比例的量。
体验总结、反思提升
你能举出生活中正比例关系的例子吗?
正方形的周长与边长成正比例关系。
如果汽车行驶速度一定,路程与时间成正比例关系。
1.一辆汽车行驶的时间和路程如下表。
时间/时 1 2 3 4 5 6
路程/km 80 160 240 320 400 480
(1)写出几组路程与相对应的时间的比,并比较比值的大小。
80 ∶1 160 ∶2 240 ∶3
320 ∶4 400 ∶5 480 ∶6 比值相等(一定)。
(2)说一说这个比值表示什么。
这个比值表示速度。
知识点 1
正比例的意义及图象
(3)汽车行驶的路程与时间成正比例关系吗?为什么?
成正比例关系。因为路程随着时间的变化而变化,而且 =速度(一定),所以成正比例关系。
路程
时间
(4)在图中描出表示路程和相对应时间的点,然后把它们按顺序连起来。并估计一下行驶120 km大约要用多少时间。
行驶120 km大约要用1.5时。
2.判断下面各题中的两种量是否成正比例关系,并说明理由。
(1)三角形的底一定,面积和高。
因为( )÷( )=底(一定)
所以( )和( )成正比例关系。
知识点 2
正比例关系的判断方法
面积×2
高
面积
高
(2)成活率一定,栽树的数量和成活的数量。
(3)圆的面积和它的半径。
3.判断。(对的画“√”,错的画“×”)
(1)在梯形中,面积与上底成正比例关系。 ( )
易错辨析
辨析:如果梯形的高一定,那么面积与上下底的
和成正比例关系;如果梯形的上下底的和一定,
那么面积与高成正比例关系。
(2)正方体的棱长和表面积成正比例关系。 ( )
辨析:正方体的棱长和表面积不成正比例关系,
因为表面积÷棱长=棱长×6(不一定)。
4.下表关于正方体的一些数量,哪两种量成正比例关系?说明理由。
提升点
正确判断正方体中的两种量是否成正比例关系
正方体的表面积和底面积成正比例关系。
因为表面积÷底面积=6。
正方体的质量与体积成正比例关系。
因为质量÷体积=每立方厘米的质量(一定)。
5.如果3x=8y,那么x和y成什么比例关系?请说明理由。
这节课你有哪些收获?
我的收获
正比例:
1. 像这样,两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系。
判断两个量是否成正比例关系的基本步骤:
一看是不是(相关联)。
二看是不是(变化相一致)。
三看是不是(商一定)
我的收获
正比例图象的特点:
正比例关系的图象是一条直的线。从图象中可以直观地看到相对应两种量的变化情况。不用计算,由一种量的值可以直接找到相对应的另一种量的值。
我的收获
必做作业 请完成教材第49页练习九第1题、第3题、第4题;第50页第5题、第7题。
选做作业 请完成教材第49页练习九第2题、下发习题集
作业设计
正比例
人教版 六年级下册第四单元第四课时
问题导入、课前热身
我们还学过哪些数量关系式?试着说一说…
已知路程和时间,怎样求速度?
速度 = 路程÷时间
已知总价和数量,怎样求单价?
单价 = 总价÷数量
已知工作总量和工作时间,怎样求工作效率?
工作效率 =工作总量÷工作时间
小红在购物,购物的时候你能想起哪个数量关系式?它们的关系还有哪种说法?进入到我们今天的学习,来看教材。
自主学习、新知引入
请仔细阅读课本第45页例1的内容,回答里面的问题。
自主学习、精读教材
数量/m 1 2 3 4 5 6 7 8 …
总价/元 3.5 7 10.5 14 17.5 21 24.5 28 …
文具店有一种彩带,销售的数量与总价的关系如下表。
观察表格中的信息,回答这三个问题。
你能知道哪些信息?
就是总价和数量是有关系的两个量。
数量/m 1 2 3 4 5 6 7 8 …
总价/元 3.5 7 10.5 14 17.5 21 24.5 28 …
(1)表中有哪两种量
数量和总价
总价和数量是两种相关联的量
数量增加,总价随着增加。
数量减少,总价随着减少。
(2)总价是怎样随着数量的变化而变化的?
合作探究、初步感知
(3)相应的总价与数量的比分别是多少?比值是多少?
数量/m 1 2 3 4 5 6 7 8 …
总价/元 3.5 7 10.5 14 17.5 21 24.5 28 …
3.5
3.5
3.5
3.5
3.5
3.5
3.5
3.5
…
=
=
=
=
=
=
=
=
比值是3.5,实际就是彩带的单价。用式子表示为:
数量
总价
=
单价
相对应的总价和数量的比的比值是一定的。
单价是固定不变的量,也就是单价一定。
合作探究、明辨释疑
小组讨论:两种量成正比例关系要满足什么条件?
合作探究、明辨释疑
指的是数量和总价
总价随着数量的变化而变化
比值都是3.5
满足这三个条件
也就是上表中“总价和数量”是成正比例的量,总价与数量成正比例关系。
展示交流、建构新知
x
y
= k(一定)
所有符合这个式子要求的两个量,就是成正比例的量。
比如“问题导入”里提到的两个量,都是成正比例的量。
速度 = 路程÷时间
单价 = 总价÷数量
工作效率 = 工作总量÷工作时间
想一想是怎么判断的?
如果用字母y和x表示两种相关联的量,用k表示它们的比值(一定),正比例关系可以用下面的式子表示:
本题表中的数据还可以用图象表示:
数量/m 1 2 3 4 5 6 7 8 …
总价/元 3.5 7 10.5 14 17.5 21 24.5 28 …
你会观察这个图象了吗?试着根据这个图象回答下面的问题:
(1)从图中你发现了什么
答:这个图象是一条逐渐上升的直的线。
层层深入、感知图像
答:这两个点也在这条射线上,并且射线又在上升,它们的单价相等。
(2)把数对(10,35)和(12,42)所在的点描出来,并和上面的图象连起来并延长,你还能发现什么
(3)不计算,根据图象判断,如果买9 m彩带,总价是多少?49元能买多少米彩带
答:通过观察,我发现买9 m彩带总价是31.5元,49元能买14 m彩带。
31.5
31.5
(4)小明买的彩带的米数是小丽的2倍,他花的钱是小丽的几倍?
答:因为彩带的数量成倍地增加,总价也会成倍地增加,所以他花的钱是小丽的2倍。
彩带的单价一定
这样的例子还有很多,想一想你学过的数量关系式和计算公式,说说成正比例的量。
体验总结、反思提升
你能举出生活中正比例关系的例子吗?
正方形的周长与边长成正比例关系。
如果汽车行驶速度一定,路程与时间成正比例关系。
1.一辆汽车行驶的时间和路程如下表。
时间/时 1 2 3 4 5 6
路程/km 80 160 240 320 400 480
(1)写出几组路程与相对应的时间的比,并比较比值的大小。
80 ∶1 160 ∶2 240 ∶3
320 ∶4 400 ∶5 480 ∶6 比值相等(一定)。
(2)说一说这个比值表示什么。
这个比值表示速度。
知识点 1
正比例的意义及图象
(3)汽车行驶的路程与时间成正比例关系吗?为什么?
成正比例关系。因为路程随着时间的变化而变化,而且 =速度(一定),所以成正比例关系。
路程
时间
(4)在图中描出表示路程和相对应时间的点,然后把它们按顺序连起来。并估计一下行驶120 km大约要用多少时间。
行驶120 km大约要用1.5时。
2.判断下面各题中的两种量是否成正比例关系,并说明理由。
(1)三角形的底一定,面积和高。
因为( )÷( )=底(一定)
所以( )和( )成正比例关系。
知识点 2
正比例关系的判断方法
面积×2
高
面积
高
(2)成活率一定,栽树的数量和成活的数量。
(3)圆的面积和它的半径。
3.判断。(对的画“√”,错的画“×”)
(1)在梯形中,面积与上底成正比例关系。 ( )
易错辨析
辨析:如果梯形的高一定,那么面积与上下底的
和成正比例关系;如果梯形的上下底的和一定,
那么面积与高成正比例关系。
(2)正方体的棱长和表面积成正比例关系。 ( )
辨析:正方体的棱长和表面积不成正比例关系,
因为表面积÷棱长=棱长×6(不一定)。
4.下表关于正方体的一些数量,哪两种量成正比例关系?说明理由。
提升点
正确判断正方体中的两种量是否成正比例关系
正方体的表面积和底面积成正比例关系。
因为表面积÷底面积=6。
正方体的质量与体积成正比例关系。
因为质量÷体积=每立方厘米的质量(一定)。
5.如果3x=8y,那么x和y成什么比例关系?请说明理由。
这节课你有哪些收获?
我的收获
正比例:
1. 像这样,两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系。
判断两个量是否成正比例关系的基本步骤:
一看是不是(相关联)。
二看是不是(变化相一致)。
三看是不是(商一定)
我的收获
正比例图象的特点:
正比例关系的图象是一条直的线。从图象中可以直观地看到相对应两种量的变化情况。不用计算,由一种量的值可以直接找到相对应的另一种量的值。
我的收获
必做作业 请完成教材第49页练习九第1题、第3题、第4题;第50页第5题、第7题。
选做作业 请完成教材第49页练习九第2题、下发习题集
作业设计
