沪科版数学七年级下册同步课件:6.2 第1课时 实数及其分类
文档属性
| 名称 | 沪科版数学七年级下册同步课件:6.2 第1课时 实数及其分类 |

|
|
| 格式 | pptx | ||
| 文件大小 | 280.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-29 00:00:00 | ||
图片预览




文档简介
(共20张PPT)
第6章 实数
6.2 第1课时 实数及其分类
知识回顾
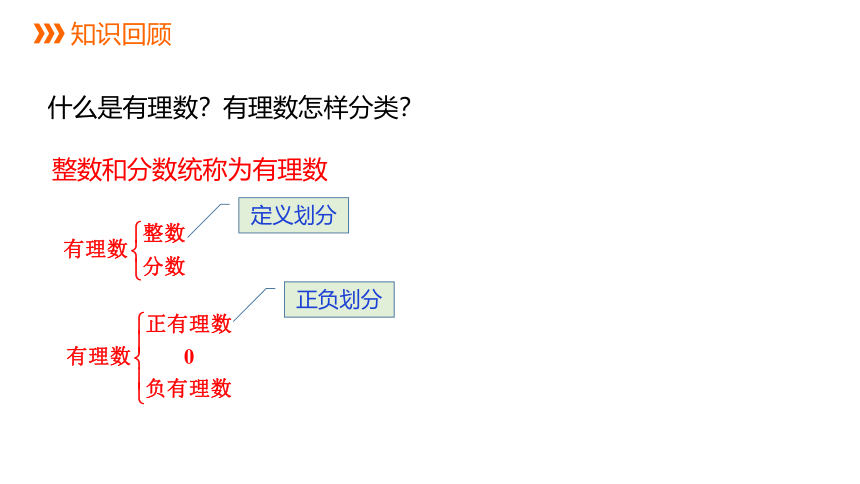
什么是有理数?有理数怎样分类?
整数和分数统称为有理数
定义划分
正负划分
获取新知
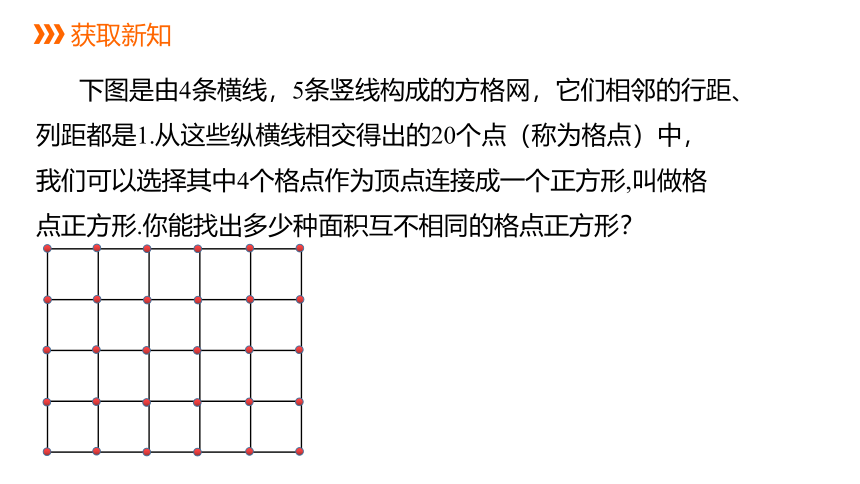
下图是由4条横线,5条竖线构成的方格网,它们相邻的行距、列距都是1.从这些纵横线相交得出的20个点(称为格点)中,我们可以选择其中4个格点作为顶点连接成一个正方形,叫做格点正方形.你能找出多少种面积互不相同的格点正方形?
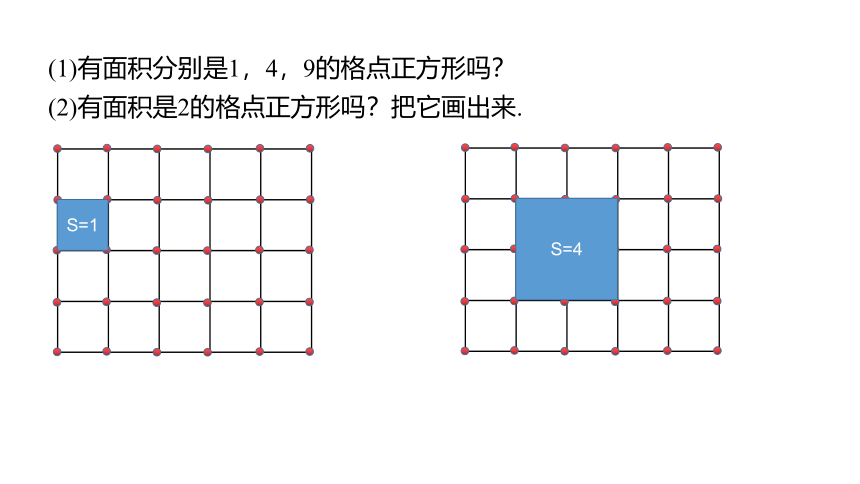
(1)有面积分别是1,4,9的格点正方形吗?
(2)有面积是2的格点正方形吗?把它画出来.
S=1
S=4
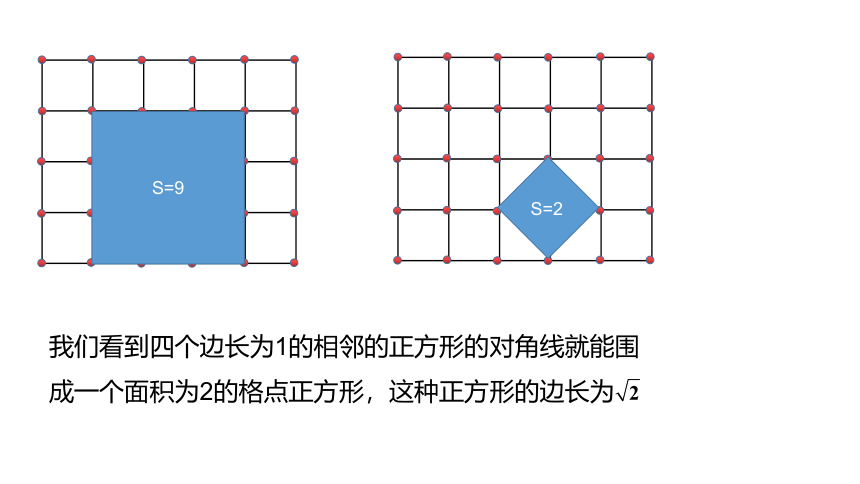
S=9
S=2
我们看到四个边长为1的相邻的正方形的对角线就能围成一个面积为2的格点正方形,这种正方形的边长为
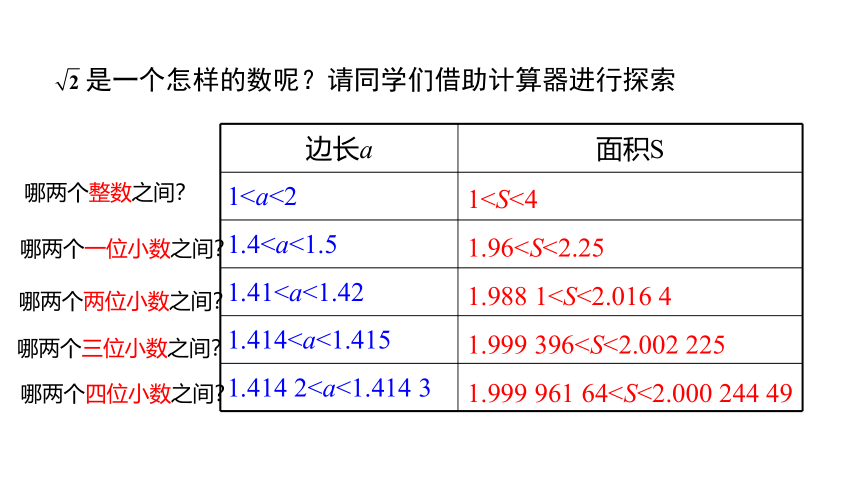
是一个怎样的数呢?请同学们借助计算器进行探索
边长a 面积S
11.41.411.4141.414 211.961.988 11.999 3961.999 961 64哪两个整数之间?
哪两个一位小数之间?
哪两个两位小数之间?
哪两个三位小数之间?
哪两个四位小数之间?
像这样一直无限做下去,我们可以得到:
我们知道,有理数包括整数和分数,整数和分数可统一写成分数的形式(整数可以看作分母为1的分数).也就是说,有理数总可写成 (m,n是整数,且m≠0)的形式.
例如,
2= = 2.0; = 0.5;
任何整数、分数都可以化为有限小数或无限循环小数.
反过来,任何有限小数和无限循环小数都可以写成分数 形式,因此有理数是有限小数或无限循环小数.
是一个无限不循环小数,它不是有理数.此外 =1.732 050 80…,
=1.442 249 57…,
π = 3. 141 592 65… .
这些数都是无限不循环小数.
我们把无限不循环小数叫作无理数.
三种常见形式:
(1)开方开不尽的数,如 , ,…;
(2)含有π的一类数: π, π,π+1,…;
(3)类似0.101 001 000 1…(每相邻两个1之间依次多1个0)
这样的无限不循环小数.
有理数和无理数统称实数
仿照有理数的分类你能给实数分类吗?
(1)按定义分类:
实数
有理数
无理数
整数
分数
有限小数或
无限循环小数
无限不循环小数
实数
正实数
负实数
0
正有理数
正无理数
负有理数
负无理数
(2)按正、负性质分类:
例1 设n为正整数,且n< <n+1,则n的值为( )
A.5 B.6 C.7 D.8
例题讲解
方法总结:开不尽的平方根形式的无理数的估算一般步骤是首先将原数平方,看其在哪两个相邻的平方数之间,运用这种方法可以估计一个带根号的数的整数部分,估计其大致范围.
D
例2 将下列各数分别填入下列相应的括号内:
无理数:
有理数:
正实数:
负实数:
注意最后要有省略号代表没有尽头
随堂演练
1.有理数和无理数的区别在于( )
A.有理数是有限小数,无理数是无限小数
B.有理数能用分数表示,而无理数不能
C.有理数是正数,无理数是负数
D.有理数是整数,无理数是分数
D
2. 下列各数:3.141 59, ,0.131 131 113…(每相邻两个3之间依次多1个1),-π, , 中,无理数有( )
A.1个 B.2个
C.3个 D.4个
B
A.AO上 B.OB上 C.BC上 D.CD上
3. 如图,已知数轴上的点A,B,C,D分别表示数-2,1,2,3,
则表示数3- 的点P应落在线段( )
B
4. 任何一个有理数都可以写成_________________________的形式,反过来,任何_________________________都是有理数.
有限小数或无限循环小数
有限小数或无限循环小数
5.按大小分,实数可分为________、______、________三类.
正实数
0
负实数
6. 把下列各数填入相应的大括号内:
-7,0.32, ,3.14,0, , ,0.101 001 000 1…
(相邻两个1之间0的个数逐次加1), , .
有理数:{ …};
无理数:{
…};
·
-7,0.32, ,3.14,0,
, ,0.101 001 000 1…(相邻两个1之间0的个数逐次加1),
, ,
·
正实数:{
…};
实数:{
…}.
·
0.32, ,3.14, , , 0.101 001 000 1
…(相邻两个1之间0的个数逐次加1), ,
-7,0.32, ,3.14,0 , , ,0.101 001 000 1…
(相邻两个1之间0的个数逐次加1), , ,
.
课堂小结
→
无理数
带省略号且不循环的小数
含有π的一类数
开方开不尽的数
概念
实数
有理数
第6章 实数
6.2 第1课时 实数及其分类
知识回顾
什么是有理数?有理数怎样分类?
整数和分数统称为有理数
定义划分
正负划分
获取新知
下图是由4条横线,5条竖线构成的方格网,它们相邻的行距、列距都是1.从这些纵横线相交得出的20个点(称为格点)中,我们可以选择其中4个格点作为顶点连接成一个正方形,叫做格点正方形.你能找出多少种面积互不相同的格点正方形?
(1)有面积分别是1,4,9的格点正方形吗?
(2)有面积是2的格点正方形吗?把它画出来.
S=1
S=4
S=9
S=2
我们看到四个边长为1的相邻的正方形的对角线就能围成一个面积为2的格点正方形,这种正方形的边长为
是一个怎样的数呢?请同学们借助计算器进行探索
边长a 面积S
1
哪两个一位小数之间?
哪两个两位小数之间?
哪两个三位小数之间?
哪两个四位小数之间?
像这样一直无限做下去,我们可以得到:
我们知道,有理数包括整数和分数,整数和分数可统一写成分数的形式(整数可以看作分母为1的分数).也就是说,有理数总可写成 (m,n是整数,且m≠0)的形式.
例如,
2= = 2.0; = 0.5;
任何整数、分数都可以化为有限小数或无限循环小数.
反过来,任何有限小数和无限循环小数都可以写成分数 形式,因此有理数是有限小数或无限循环小数.
是一个无限不循环小数,它不是有理数.此外 =1.732 050 80…,
=1.442 249 57…,
π = 3. 141 592 65… .
这些数都是无限不循环小数.
我们把无限不循环小数叫作无理数.
三种常见形式:
(1)开方开不尽的数,如 , ,…;
(2)含有π的一类数: π, π,π+1,…;
(3)类似0.101 001 000 1…(每相邻两个1之间依次多1个0)
这样的无限不循环小数.
有理数和无理数统称实数
仿照有理数的分类你能给实数分类吗?
(1)按定义分类:
实数
有理数
无理数
整数
分数
有限小数或
无限循环小数
无限不循环小数
实数
正实数
负实数
0
正有理数
正无理数
负有理数
负无理数
(2)按正、负性质分类:
例1 设n为正整数,且n< <n+1,则n的值为( )
A.5 B.6 C.7 D.8
例题讲解
方法总结:开不尽的平方根形式的无理数的估算一般步骤是首先将原数平方,看其在哪两个相邻的平方数之间,运用这种方法可以估计一个带根号的数的整数部分,估计其大致范围.
D
例2 将下列各数分别填入下列相应的括号内:
无理数:
有理数:
正实数:
负实数:
注意最后要有省略号代表没有尽头
随堂演练
1.有理数和无理数的区别在于( )
A.有理数是有限小数,无理数是无限小数
B.有理数能用分数表示,而无理数不能
C.有理数是正数,无理数是负数
D.有理数是整数,无理数是分数
D
2. 下列各数:3.141 59, ,0.131 131 113…(每相邻两个3之间依次多1个1),-π, , 中,无理数有( )
A.1个 B.2个
C.3个 D.4个
B
A.AO上 B.OB上 C.BC上 D.CD上
3. 如图,已知数轴上的点A,B,C,D分别表示数-2,1,2,3,
则表示数3- 的点P应落在线段( )
B
4. 任何一个有理数都可以写成_________________________的形式,反过来,任何_________________________都是有理数.
有限小数或无限循环小数
有限小数或无限循环小数
5.按大小分,实数可分为________、______、________三类.
正实数
0
负实数
6. 把下列各数填入相应的大括号内:
-7,0.32, ,3.14,0, , ,0.101 001 000 1…
(相邻两个1之间0的个数逐次加1), , .
有理数:{ …};
无理数:{
…};
·
-7,0.32, ,3.14,0,
, ,0.101 001 000 1…(相邻两个1之间0的个数逐次加1),
, ,
·
正实数:{
…};
实数:{
…}.
·
0.32, ,3.14, , , 0.101 001 000 1
…(相邻两个1之间0的个数逐次加1), ,
-7,0.32, ,3.14,0 , , ,0.101 001 000 1…
(相邻两个1之间0的个数逐次加1), , ,
.
课堂小结
→
无理数
带省略号且不循环的小数
含有π的一类数
开方开不尽的数
概念
实数
有理数
