沪科版数学七年级下册:6.2 第2课时 实数的运算及大小比较 同步课件(共22张PPT)
文档属性
| 名称 | 沪科版数学七年级下册:6.2 第2课时 实数的运算及大小比较 同步课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 422.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-29 00:00:00 | ||
图片预览








文档简介
(共22张PPT)
第6章 实数
6.2 第2课时 实数的运算及大小比较
知识回顾
下列各数中,哪些是有理数,哪些是无理数?
, 0, 1.414, , , ,
, 0.1010010001…(相邻两个1之间逐次增加一个0).
是有理数,
是无理数.
思考:有理数可以做加、减、乘、除、乘方运算,实数可以吗?
获取新知
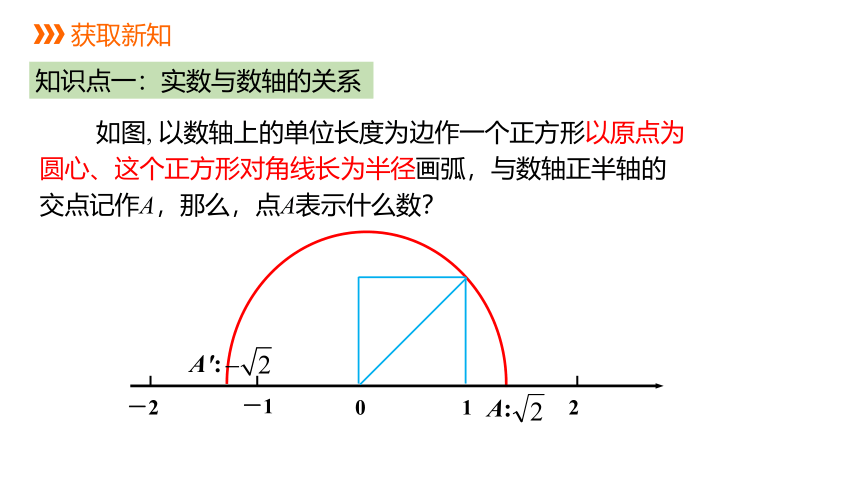
知识点一:实数与数轴的关系
如图, 以数轴上的单位长度为边作一个正方形以原点为圆心、这个正方形对角线长为半径画弧,与数轴正半轴的交点记作A,那么,点A表示什么数?
-2
-1
0
1
2
A:
A':
归纳总结
实数与数轴上点间的关系(数与形)
实数和数轴上的点是一一对应的
1.每一个实数都可以用数轴上的一个点来表示;
2.数轴上的每一点都表示一个实数.
在实数范围内 ,相反数、倒数、绝对值的意义和有理数范围内的相反数、倒数、绝对值的意义完全一样.
例如, 互为相反数
任一个实数a的绝对值仍然用|a|表示,如
互为倒数
例题讲解
例1 (1)分别写出 , 的相反数;
(2)指出 , 分别是什么数的相反数;
(3)求 的绝对值;
(4)已知一个数的绝对值是 ,求这个数.
(1)因为 ,
所以 的相反数分别为 ;
(2)因为 ,
所以 分别是 的相反数;
(3)因为 ,
所以 ;
(4)因为 ,
所以绝对值为 的数是 或 .
解:
获取新知
知识点二:实数的运算
1.运算类型:加、减、乘、除、乘方和开方运算(开平方仅限非负数)
在实数范围内
2.运算法则:与有理数的运算法则相同
3.运算律:有理数的运算律在实数范围同样适用
4.运算顺序:先算乘方、开方,再算乘除,最后算加减,同级运算按照自左向右的顺序进行,有括号的先算括号里面的
例题讲解
例2 近似计算:
(1) (精确到0.01);
(2) (精确到0.1);
解:(1) 1.732+3.142=4.874≈4.87;
(2) 2.24×2.65=5.936≈5.9;
例3 计算下列各式的值:
(1) ; (2) .
解:(1)
(2)
(加法结合律)
(逆用分配律)
获取新知
知识点三:实数的大小比较
与有理数规定的大小一样,数轴上右边的点表示的实数比左边的点表示的实数大.
原点
0
正实数
负实数
<
1.正数大于零,负数小于零,正数大于负数;
2.两个正数,绝对值大的数较大;
3.两个负数,绝对值大的数反而小.
与有理数一样,在实数范围内:
例4 在数轴上作出表示下列各数的点,比较它们的大小,并用“<”连接它们.
例题讲解
由数轴上各点的位置,得
解:
例5 比较下列各组数的大小:
解 :(1)因为 12 < 42,
所以 < 4,
所以 -1< 3;
(2)因为 10 > 32 ,
所以
所以
随堂演练
1. 如图,数轴上的A,B,C,D四点中,与数- 对应的点最接近的是( )
A.点A B.点B C.点C D.点D
B
2. 下列四个数:-3,- ,-π,-1,其中最小的数是( )
A.-π B.-3
C.-1 D.-
A
3.下列各数中,互为相反数的是( )
C
4. 的值是( )
A.5 B.-1 C. D.
C
5.如图所示,数轴上A,B两点表示的数分别为 和5.1,则A,B两点之间表示整数的点共有___个
4
6. 用“<”连接下列各数: , ,- ,2.5,0.
由图可知,各数用“<”可以连接成:
- < <0< <2.5.
解:将各数的大致位置在数轴上表示出来,如图所示.
解:(1)
(2)
(3)
7.用计算器计算(精确到0.01):
(1) ; (2) ; (3) .
8. 计算:
解:
课堂小结
实数
在实数范围内,相反数、绝对值、倒数的意义和有理数范围内的相反数、绝对值、倒数的意义完全一样.
实数与数轴上点的一一对应
实数的运算
实数的运算律
用计算器计算
实数的大小比较
第6章 实数
6.2 第2课时 实数的运算及大小比较
知识回顾
下列各数中,哪些是有理数,哪些是无理数?
, 0, 1.414, , , ,
, 0.1010010001…(相邻两个1之间逐次增加一个0).
是有理数,
是无理数.
思考:有理数可以做加、减、乘、除、乘方运算,实数可以吗?
获取新知
知识点一:实数与数轴的关系
如图, 以数轴上的单位长度为边作一个正方形以原点为圆心、这个正方形对角线长为半径画弧,与数轴正半轴的交点记作A,那么,点A表示什么数?
-2
-1
0
1
2
A:
A':
归纳总结
实数与数轴上点间的关系(数与形)
实数和数轴上的点是一一对应的
1.每一个实数都可以用数轴上的一个点来表示;
2.数轴上的每一点都表示一个实数.
在实数范围内 ,相反数、倒数、绝对值的意义和有理数范围内的相反数、倒数、绝对值的意义完全一样.
例如, 互为相反数
任一个实数a的绝对值仍然用|a|表示,如
互为倒数
例题讲解
例1 (1)分别写出 , 的相反数;
(2)指出 , 分别是什么数的相反数;
(3)求 的绝对值;
(4)已知一个数的绝对值是 ,求这个数.
(1)因为 ,
所以 的相反数分别为 ;
(2)因为 ,
所以 分别是 的相反数;
(3)因为 ,
所以 ;
(4)因为 ,
所以绝对值为 的数是 或 .
解:
获取新知
知识点二:实数的运算
1.运算类型:加、减、乘、除、乘方和开方运算(开平方仅限非负数)
在实数范围内
2.运算法则:与有理数的运算法则相同
3.运算律:有理数的运算律在实数范围同样适用
4.运算顺序:先算乘方、开方,再算乘除,最后算加减,同级运算按照自左向右的顺序进行,有括号的先算括号里面的
例题讲解
例2 近似计算:
(1) (精确到0.01);
(2) (精确到0.1);
解:(1) 1.732+3.142=4.874≈4.87;
(2) 2.24×2.65=5.936≈5.9;
例3 计算下列各式的值:
(1) ; (2) .
解:(1)
(2)
(加法结合律)
(逆用分配律)
获取新知
知识点三:实数的大小比较
与有理数规定的大小一样,数轴上右边的点表示的实数比左边的点表示的实数大.
原点
0
正实数
负实数
<
1.正数大于零,负数小于零,正数大于负数;
2.两个正数,绝对值大的数较大;
3.两个负数,绝对值大的数反而小.
与有理数一样,在实数范围内:
例4 在数轴上作出表示下列各数的点,比较它们的大小,并用“<”连接它们.
例题讲解
由数轴上各点的位置,得
解:
例5 比较下列各组数的大小:
解 :(1)因为 12 < 42,
所以 < 4,
所以 -1< 3;
(2)因为 10 > 32 ,
所以
所以
随堂演练
1. 如图,数轴上的A,B,C,D四点中,与数- 对应的点最接近的是( )
A.点A B.点B C.点C D.点D
B
2. 下列四个数:-3,- ,-π,-1,其中最小的数是( )
A.-π B.-3
C.-1 D.-
A
3.下列各数中,互为相反数的是( )
C
4. 的值是( )
A.5 B.-1 C. D.
C
5.如图所示,数轴上A,B两点表示的数分别为 和5.1,则A,B两点之间表示整数的点共有___个
4
6. 用“<”连接下列各数: , ,- ,2.5,0.
由图可知,各数用“<”可以连接成:
- < <0< <2.5.
解:将各数的大致位置在数轴上表示出来,如图所示.
解:(1)
(2)
(3)
7.用计算器计算(精确到0.01):
(1) ; (2) ; (3) .
8. 计算:
解:
课堂小结
实数
在实数范围内,相反数、绝对值、倒数的意义和有理数范围内的相反数、绝对值、倒数的意义完全一样.
实数与数轴上点的一一对应
实数的运算
实数的运算律
用计算器计算
实数的大小比较
