沪科版数学七年级下册同步课件:7.1 第2课时 不等式的基本性质
文档属性
| 名称 | 沪科版数学七年级下册同步课件:7.1 第2课时 不等式的基本性质 |

|
|
| 格式 | pptx | ||
| 文件大小 | 573.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-29 10:03:28 | ||
图片预览








文档简介
(共20张PPT)
第7章 一元一次不等式与不等式组
7.1 第2课时 不等式的基本性质
知识回顾
前面我们已经学习过等式的基本性质
(1)等式的两边加或减同一个数(或式子),
等式仍然成立.
(2)等式的两边乘或除以同一个数(除数不
为0),等式仍然成立.
猜想 :不等式也具有同样的性质吗?
获取新知
观察
如图,在一台天平两端的托盘中分别放置了质量为a,b的物体,图中天平倾斜,这直观地说明a>b.
这时,如果在两端托盘中同时加上质量为c的物体,天平的倾斜方向会改变吗?这反映的数量关系是什么呢?
如果a>b,那么a+c>b+c,a-c>b-c.
不等式的性质1 不等式两边加(或减)同一个数或同一个整式 ,不等号的方向不变.
思考
对于倾斜的天平,如果两边砝码的质量同时扩大相同的倍数或同时缩小为原来的几分之一,那么 天平的倾斜方向会改变吗?
不等式的性质2 不等式两边乘(或除以)同一个正数,
不等号的方向不变.
如果a > b,c > 0,那么 ac > bc , >
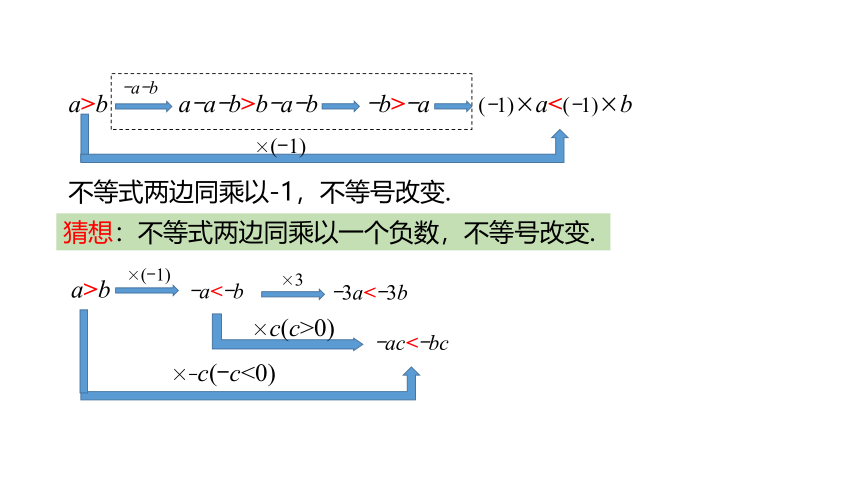
a>b
-a-b
a-a-b>b-a-b
-b>-a
(-1)×a<(-1)×b
×(-1)
不等式两边同乘以-1,不等号改变.
猜想:不等式两边同乘以一个负数,不等号改变.
a>b
×(-1)
-a<-b
×3
-3a<-3b
×c(c>0)
-ac<-bc
×-c(-c<0)
不等式的性质3 不等式两边乘(或除以)同一个负数,
不等号的方向改变.
如果a > b,c < 0,那么 ac < bc , <
不等式的性质4 如果a>b,那么,b<a.
不等式的性质5 如果a>b, b>c,那么a>c.
例题讲解
解:因为 a>b,两边都加上3,
由不等式基本性质1,得
a+3 > b+3;
由不等式基本性质1,得
a-5 < b-5 .
(1)已知 a>b,则a+3 b+3
(2)已知 a>
<
例1 用“>”或“<”填空:
因为 a>b,两边都乘3,
由不等式基本性质2,得
3a > 3b.
(3)已知 a>b,则3a 3b ;
因为 a由不等式基本性质3,得
由不等式基本性质1,得
(4)已知 a因为 ,两边都加上2,
>
>
例2 利用不等式的性质解下列不等式:
(1)x-7>26; (2) 3x<2x+1;
(3) x>50; (4) -4x>3.
解未知数为x的不等式
化为x>a或x目标
方法:不等式基本性质1~3
思路:
解:(1)根据不等式的性质1,不等式两边加7, 不等号的方向不变,所以
x-7+7>26+7,
x>33.
(2)根据不等式的性质1,不等式两边减2x,不等号的方向不变,所以
3x-2x<2x+1-2x,
x<1.
(3)根据不等式的性质2, 不等式两边乘 . 不等号的方向不变,所以
x>75.
(4)根据不等式的性质3, 不等式两边除以-4, 不等号的方向改变,所以
随堂演练
1. 已知实数a、b ,若a>b ,则下列结论正确的是( )
A.a-5<b-5 B.2+a<2+b
C. D.3a>3b
D
2.若3x>-3y,则下列不等式中一定成立的是( )
A.x+y>0 B.x-y>0
C.x+y<0 D.x-y<0
A
3.设a>b,用“<”“>”填空并回答是根据不等式的哪一条基本性质.
(1) a - 7____b - 7;根据是__________________
(2) a÷6____b÷6;根据是__________________
(3) 0.1a____0.1b; 根据是__________________
(4) -4a____-4b;根据是__________________
(5) 2a+3____2b+3;根据是__________________
(6)(m2+1)a____ (m2+1)b(m为常数);根据是__________________
>
>
>
>
>
<
不等式的性质1
不等式的性质2
不等式的性质2
不等式的性质3
不等式的性质1,2
不等式的性质2
4. 如果不等式 (a+1)x<a+1可变形为 x>1,那么a 必须满足________.
a<-1
5.把下列不等式化成“x>a”或“x<a”的形式.
(1)2x-2<0;(2)3x-9<6x;(3) x-2> x-5.
解:(1)根据不等式的基本性质1,
两边都加上2得:2x<2.
根据不等式的基本性质2,
两边除以2得:x<1;
(2)根据不等式的基本性质1,
两边都加上9-6x得:-3x<9.
根据不等式的基本性质3,
两边都除以-3得:x>-3;
(3)根据不等式的基本性质1,
两边都加上2- x得:-x>-3.
根据不等式的基本性质3,
两边都除以-1得:x<3.
课堂小结
性质1:如果a >b,那么a±c>b±c
不等式的概念
不等式的基本性质
性质4:如果a>b,那么b性质5:如果a>b,b>c,那么a>c.
不等式
性质2:如果a >b,c > 0 ,
那么 ac>bc(或 )
性质3:如果a>b,c<0 ,
那么ac
第7章 一元一次不等式与不等式组
7.1 第2课时 不等式的基本性质
知识回顾
前面我们已经学习过等式的基本性质
(1)等式的两边加或减同一个数(或式子),
等式仍然成立.
(2)等式的两边乘或除以同一个数(除数不
为0),等式仍然成立.
猜想 :不等式也具有同样的性质吗?
获取新知
观察
如图,在一台天平两端的托盘中分别放置了质量为a,b的物体,图中天平倾斜,这直观地说明a>b.
这时,如果在两端托盘中同时加上质量为c的物体,天平的倾斜方向会改变吗?这反映的数量关系是什么呢?
如果a>b,那么a+c>b+c,a-c>b-c.
不等式的性质1 不等式两边加(或减)同一个数或同一个整式 ,不等号的方向不变.
思考
对于倾斜的天平,如果两边砝码的质量同时扩大相同的倍数或同时缩小为原来的几分之一,那么 天平的倾斜方向会改变吗?
不等式的性质2 不等式两边乘(或除以)同一个正数,
不等号的方向不变.
如果a > b,c > 0,那么 ac > bc , >
a>b
-a-b
a-a-b>b-a-b
-b>-a
(-1)×a<(-1)×b
×(-1)
不等式两边同乘以-1,不等号改变.
猜想:不等式两边同乘以一个负数,不等号改变.
a>b
×(-1)
-a<-b
×3
-3a<-3b
×c(c>0)
-ac<-bc
×-c(-c<0)
不等式的性质3 不等式两边乘(或除以)同一个负数,
不等号的方向改变.
如果a > b,c < 0,那么 ac < bc , <
不等式的性质4 如果a>b,那么,b<a.
不等式的性质5 如果a>b, b>c,那么a>c.
例题讲解
解:因为 a>b,两边都加上3,
由不等式基本性质1,得
a+3 > b+3;
由不等式基本性质1,得
a-5 < b-5 .
(1)已知 a>b,则a+3 b+3
(2)已知 a
<
例1 用“>”或“<”填空:
因为 a>b,两边都乘3,
由不等式基本性质2,得
3a > 3b.
(3)已知 a>b,则3a 3b ;
因为 a
由不等式基本性质1,得
(4)已知 a
>
>
例2 利用不等式的性质解下列不等式:
(1)x-7>26; (2) 3x<2x+1;
(3) x>50; (4) -4x>3.
解未知数为x的不等式
化为x>a或x
方法:不等式基本性质1~3
思路:
解:(1)根据不等式的性质1,不等式两边加7, 不等号的方向不变,所以
x-7+7>26+7,
x>33.
(2)根据不等式的性质1,不等式两边减2x,不等号的方向不变,所以
3x-2x<2x+1-2x,
x<1.
(3)根据不等式的性质2, 不等式两边乘 . 不等号的方向不变,所以
x>75.
(4)根据不等式的性质3, 不等式两边除以-4, 不等号的方向改变,所以
随堂演练
1. 已知实数a、b ,若a>b ,则下列结论正确的是( )
A.a-5<b-5 B.2+a<2+b
C. D.3a>3b
D
2.若3x>-3y,则下列不等式中一定成立的是( )
A.x+y>0 B.x-y>0
C.x+y<0 D.x-y<0
A
3.设a>b,用“<”“>”填空并回答是根据不等式的哪一条基本性质.
(1) a - 7____b - 7;根据是__________________
(2) a÷6____b÷6;根据是__________________
(3) 0.1a____0.1b; 根据是__________________
(4) -4a____-4b;根据是__________________
(5) 2a+3____2b+3;根据是__________________
(6)(m2+1)a____ (m2+1)b(m为常数);根据是__________________
>
>
>
>
>
<
不等式的性质1
不等式的性质2
不等式的性质2
不等式的性质3
不等式的性质1,2
不等式的性质2
4. 如果不等式 (a+1)x<a+1可变形为 x>1,那么a 必须满足________.
a<-1
5.把下列不等式化成“x>a”或“x<a”的形式.
(1)2x-2<0;(2)3x-9<6x;(3) x-2> x-5.
解:(1)根据不等式的基本性质1,
两边都加上2得:2x<2.
根据不等式的基本性质2,
两边除以2得:x<1;
(2)根据不等式的基本性质1,
两边都加上9-6x得:-3x<9.
根据不等式的基本性质3,
两边都除以-3得:x>-3;
(3)根据不等式的基本性质1,
两边都加上2- x得:-x>-3.
根据不等式的基本性质3,
两边都除以-1得:x<3.
课堂小结
性质1:如果a >b,那么a±c>b±c
不等式的概念
不等式的基本性质
性质4:如果a>b,那么b
不等式
性质2:如果a >b,c > 0 ,
那么 ac>bc(或 )
性质3:如果a>b,c<0 ,
那么ac
