沪科版数学七年级下册同步课件:7.2 第1课时 一元一次不等式的概念及其解法
文档属性
| 名称 | 沪科版数学七年级下册同步课件:7.2 第1课时 一元一次不等式的概念及其解法 |

|
|
| 格式 | pptx | ||
| 文件大小 | 388.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-29 10:06:19 | ||
图片预览







文档简介
(共22张PPT)
第7章 一元一次不等式与不等式组
7.2 第1课时 一元一次不等式的概念及其解法
知识回顾
1.什么叫一元一次方程
只含有一个未知数、并且未知数的次数都是1”,
等号两边都是整式,这样的方程叫做一元一次方程.
2.不等式的基本性质:
不等式性质1:不等式两边加(或减)同一个数(或式子),不等号的方向不变.
不等式性质2:不等式两边都乘(或除以)同一个正数,不等号的方向不变.
不等式性质3:不等式两边都乘(或除以)同一个负数,不等号的方向改变.
获取新知
问题
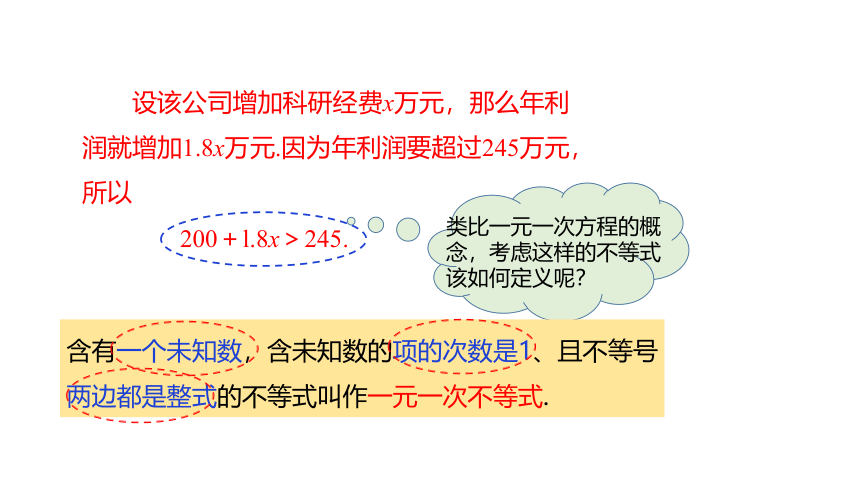
某公司的统计资料表明,科研经费每增加1万元,年利润就增加1. 8万元.如果该公司原来的年利润为200万元,要使年利润超过245万元,那么增加的科研经费应高于多少万元?
设该公司增加科研经费x万元,那么年利润就增加1.8x万元.因为年利润要超过245万元,所以
类比一元一次方程的概念,考虑这样的不等式该如何定义呢?
200+l.8x>245.
含有一个未知数,含未知数的项的次数是1、且不等号
两边都是整式的不等式叫作一元一次不等式.
对于不等式200 +1. 8x>245 :
当x取26时,代入原不等式左边,得200+1.8×26=246.8>245
当x取25时,代入原不等式左边,得200+1.8×25=245=245.
当x取24时,代入原不等式左边,得200+1.8×24=243.2<245.
1.不等式的解:能使不等式成立的未知数的值
2.不等式的解集:所有解的全体
3.解不等式:求不等式解集的过程
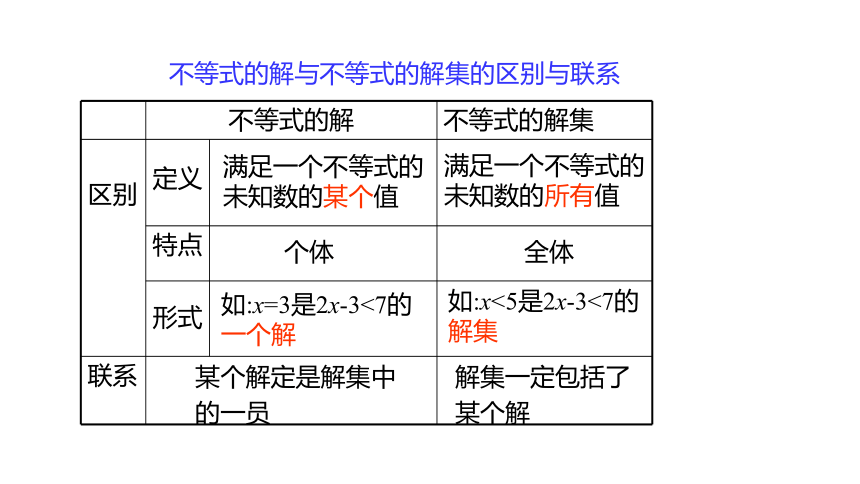
不等式的解 不等式的解集
区别 定义
特点
形式
联系
满足一个不等式的未知数的某个值
满足一个不等式的未知数的所有值
个体
全体
如:x=3是2x-3<7的一个解
如:x<5是2x-3<7的解集
某个解定是解集中
的一员
不等式的解与不等式的解集的区别与联系
解集一定包括了
某个解
例题讲解
例1 下列各数中,哪些是不等式2(2x+1)>25的解?哪些不是?
1 ;2 ;10 ;12.
分析:判断一个数是不是不等式的解,一般的方法是将该数代入不等式,验证不等式是否成立.
把x=1代入不等式2(2x+1)>25,得
2×(2×1+1)>25,即6>25,
所以x=1不能使不等式成立,
所以x=1不是不等式2(2x+1)>25的解.
同理,分别把x=2,x=10,x=12代入不等式2(2x+1)>25,可知x=2不能使不等式成立,
x=10和x=12能使不等式成立.
所以x=1和x=2不是不等式2(2x+1)>25的解,
x=10和x=12是不等式2(2x+1)>25的解.
例2 解不等式:2x+5≤7(2-x).
解:去括号,得 2x+5≤14-7x.
移项,得 2x+7x≤14-5.
合并同类项,得 9x≤9.
x系数化为1,得 x≤1.
不等式的解集在数轴上表示出来为:
-3
-2
-1
0
1
2
3
-4
例3 解不等式,并把它的解集在数轴上表示出来:
解:去分母,得2(4+x)-6<3x.
去括号,得8+2x-6<3x.
移项、合并同类项,得-x<-2.
x系数化成1,得x>2.
在数轴上表示不等式的解集(如图)
-2
-1
0
1
2
3
4
-3
类似解一元一次方程,解一元一次不等式的步骤和根据如下:
步骤 根据
1 去分母 不等式的基本性质 2
2 去括号 单项式乘以多项式法则
3 移项 不等式的基本性质 1
4 合并同类项,得ax>b,或ax5 两边同除以a(或乘 ) 不等式的基本性质2或3
用数轴表示不等式的解集的步骤:
第一步:画数轴;
第二步:定界点(包含实心点;否则空心圈);
第三步:定方向(大于向右;小于向左).
随堂演练
1.下列不等式中,是一元一次不等式的是( )
A.2x-1>0 B.-1<2
C.3x-2y≤-1 D.y2+3>5
A
2.下列不是不等式5x-3<6的一个解的是( )
A.1 B.2 C.-1 D.-2
B
3. 解不等式 的过程中,开始出现错误的一步是( )
①去分母,得5(x+2)>3(2x-1);
②去括号,得5x+10>6x-3;
③移项、合并同类项,得-x>-13;
④系数化为1,得x>13.
A.① B.② C.③ D.④
D
4. 解一元一次不等式:
解:去分母,得_____-(x+5)<3x+2.
去括号,得2-________<3x+2.
移项,得-x-_____<2-2+5.
合并同类项,得-4x<5.
系数化为1,得x>________.
2
x-5
3x
-1.25
5. 当自然数k=_________时,关于x的方程 x-3k=5(x-k)+6
的解是负数.
0,1,2
6. 解下列不等式,并在数轴上表示解集:
(1) 5x+15>4x-1;
(2) 2(x+5)≤3(x-5);
解:(1)移项,得5x-4x>-1-15,
合并同类项,得x>-16.
这个不等式的解集在数轴上的表示.
(2)去括号,得2x+10≤3x-15,
移项,得2x-3x≤-15-10,
合并同类项,得-x≤-25,
系数化为1,得x≥25.
这个不等式的解集在数轴上的表示.
-32
-24
-16
-8
0
8
16
24
-5
0
5
10
15
20
25
30
(3)去分母,得3(x-1)<2(2x+1),
去括号,得3x-3<4x+2,
移项,得3x-4x<2+3,
合并同类项,得-x<5,
系数化为1,得x>-5
这个不等式的解集在数轴上的表示为:
-5
-4
-3
-2
-1
0
1
2
(4)去分母,得2(x+1)≥(x-5)+12,
去括号,得2x+2≥x-5+12,
移项,合并同类项,得x≥5,
这个不等式的解集在数轴上的表示为:
-5
-4
-3
-2
-1
0
1
2
课堂小结
一元一次不等式
一元一次不等式的概念
解一元一次不等式
→
将解集在数轴上表示
一元一次不等式的解及其解集
第7章 一元一次不等式与不等式组
7.2 第1课时 一元一次不等式的概念及其解法
知识回顾
1.什么叫一元一次方程
只含有一个未知数、并且未知数的次数都是1”,
等号两边都是整式,这样的方程叫做一元一次方程.
2.不等式的基本性质:
不等式性质1:不等式两边加(或减)同一个数(或式子),不等号的方向不变.
不等式性质2:不等式两边都乘(或除以)同一个正数,不等号的方向不变.
不等式性质3:不等式两边都乘(或除以)同一个负数,不等号的方向改变.
获取新知
问题
某公司的统计资料表明,科研经费每增加1万元,年利润就增加1. 8万元.如果该公司原来的年利润为200万元,要使年利润超过245万元,那么增加的科研经费应高于多少万元?
设该公司增加科研经费x万元,那么年利润就增加1.8x万元.因为年利润要超过245万元,所以
类比一元一次方程的概念,考虑这样的不等式该如何定义呢?
200+l.8x>245.
含有一个未知数,含未知数的项的次数是1、且不等号
两边都是整式的不等式叫作一元一次不等式.
对于不等式200 +1. 8x>245 :
当x取26时,代入原不等式左边,得200+1.8×26=246.8>245
当x取25时,代入原不等式左边,得200+1.8×25=245=245.
当x取24时,代入原不等式左边,得200+1.8×24=243.2<245.
1.不等式的解:能使不等式成立的未知数的值
2.不等式的解集:所有解的全体
3.解不等式:求不等式解集的过程
不等式的解 不等式的解集
区别 定义
特点
形式
联系
满足一个不等式的未知数的某个值
满足一个不等式的未知数的所有值
个体
全体
如:x=3是2x-3<7的一个解
如:x<5是2x-3<7的解集
某个解定是解集中
的一员
不等式的解与不等式的解集的区别与联系
解集一定包括了
某个解
例题讲解
例1 下列各数中,哪些是不等式2(2x+1)>25的解?哪些不是?
1 ;2 ;10 ;12.
分析:判断一个数是不是不等式的解,一般的方法是将该数代入不等式,验证不等式是否成立.
把x=1代入不等式2(2x+1)>25,得
2×(2×1+1)>25,即6>25,
所以x=1不能使不等式成立,
所以x=1不是不等式2(2x+1)>25的解.
同理,分别把x=2,x=10,x=12代入不等式2(2x+1)>25,可知x=2不能使不等式成立,
x=10和x=12能使不等式成立.
所以x=1和x=2不是不等式2(2x+1)>25的解,
x=10和x=12是不等式2(2x+1)>25的解.
例2 解不等式:2x+5≤7(2-x).
解:去括号,得 2x+5≤14-7x.
移项,得 2x+7x≤14-5.
合并同类项,得 9x≤9.
x系数化为1,得 x≤1.
不等式的解集在数轴上表示出来为:
-3
-2
-1
0
1
2
3
-4
例3 解不等式,并把它的解集在数轴上表示出来:
解:去分母,得2(4+x)-6<3x.
去括号,得8+2x-6<3x.
移项、合并同类项,得-x<-2.
x系数化成1,得x>2.
在数轴上表示不等式的解集(如图)
-2
-1
0
1
2
3
4
-3
类似解一元一次方程,解一元一次不等式的步骤和根据如下:
步骤 根据
1 去分母 不等式的基本性质 2
2 去括号 单项式乘以多项式法则
3 移项 不等式的基本性质 1
4 合并同类项,得ax>b,或ax5 两边同除以a(或乘 ) 不等式的基本性质2或3
用数轴表示不等式的解集的步骤:
第一步:画数轴;
第二步:定界点(包含实心点;否则空心圈);
第三步:定方向(大于向右;小于向左).
随堂演练
1.下列不等式中,是一元一次不等式的是( )
A.2x-1>0 B.-1<2
C.3x-2y≤-1 D.y2+3>5
A
2.下列不是不等式5x-3<6的一个解的是( )
A.1 B.2 C.-1 D.-2
B
3. 解不等式 的过程中,开始出现错误的一步是( )
①去分母,得5(x+2)>3(2x-1);
②去括号,得5x+10>6x-3;
③移项、合并同类项,得-x>-13;
④系数化为1,得x>13.
A.① B.② C.③ D.④
D
4. 解一元一次不等式:
解:去分母,得_____-(x+5)<3x+2.
去括号,得2-________<3x+2.
移项,得-x-_____<2-2+5.
合并同类项,得-4x<5.
系数化为1,得x>________.
2
x-5
3x
-1.25
5. 当自然数k=_________时,关于x的方程 x-3k=5(x-k)+6
的解是负数.
0,1,2
6. 解下列不等式,并在数轴上表示解集:
(1) 5x+15>4x-1;
(2) 2(x+5)≤3(x-5);
解:(1)移项,得5x-4x>-1-15,
合并同类项,得x>-16.
这个不等式的解集在数轴上的表示.
(2)去括号,得2x+10≤3x-15,
移项,得2x-3x≤-15-10,
合并同类项,得-x≤-25,
系数化为1,得x≥25.
这个不等式的解集在数轴上的表示.
-32
-24
-16
-8
0
8
16
24
-5
0
5
10
15
20
25
30
(3)去分母,得3(x-1)<2(2x+1),
去括号,得3x-3<4x+2,
移项,得3x-4x<2+3,
合并同类项,得-x<5,
系数化为1,得x>-5
这个不等式的解集在数轴上的表示为:
-5
-4
-3
-2
-1
0
1
2
(4)去分母,得2(x+1)≥(x-5)+12,
去括号,得2x+2≥x-5+12,
移项,合并同类项,得x≥5,
这个不等式的解集在数轴上的表示为:
-5
-4
-3
-2
-1
0
1
2
课堂小结
一元一次不等式
一元一次不等式的概念
解一元一次不等式
→
将解集在数轴上表示
一元一次不等式的解及其解集
