人教版七年级数学 下册 第九章 9.2 .2一元一次不等式的应用 课件(共20张PPT)
文档属性
| 名称 | 人教版七年级数学 下册 第九章 9.2 .2一元一次不等式的应用 课件(共20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 914.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-30 15:47:02 | ||
图片预览








文档简介
(共20张PPT)
1、解一元一次不等式的一般步骤:
(1)去分母;
(2)去括号;
(3)移项;
(4)合并同类项;
(5)系数化为1.(注意不等号的方向)
知识回顾
2、列一元一次方程解决实际问题的一般步骤:
(1)审:审题,找等量关系;
(2)设:设未知数;
(3)列:列方程;
(4)解:解方程;
(5)答:根据实际情况作答.
9.2 一元一次不等式
第2课时 一元一次不等式的应用
人教版七年级数学 下册
目标导航
1.会通过列一元一次不等式去解决生活中的实际问 题,经历“实际问题抽象为不等式模型”的过程;(重点)
2.体会解不等式过程中的化归思想与类比思想,体会分类讨论思想在用不等式解决实际问题中的应用.
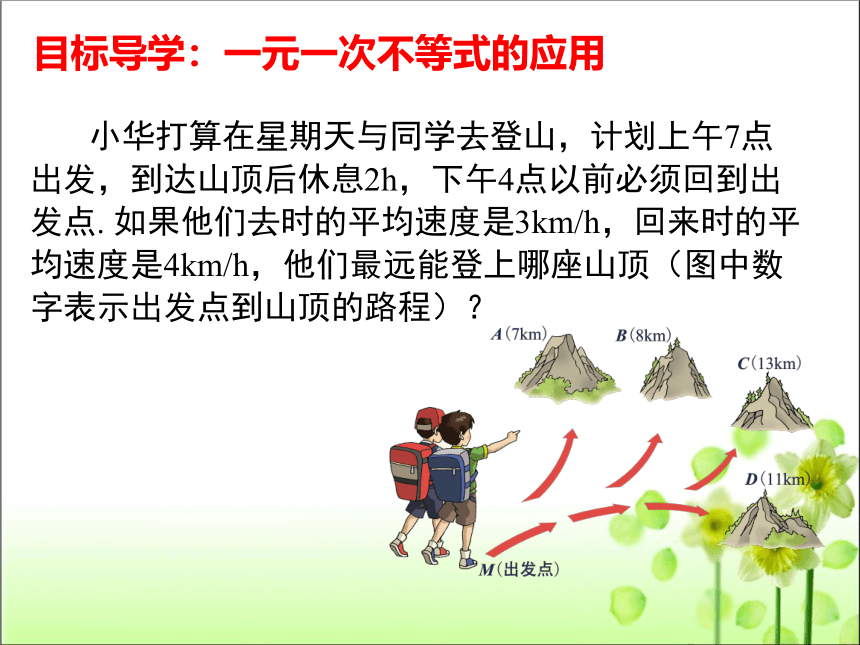
小华打算在星期天与同学去登山,计划上午7点出发,到达山顶后休息2h,下午4点以前必须回到出发点. 如果他们去时的平均速度是3km/h,回来时的平均速度是4km/h,他们最远能登上哪座山顶(图中数字表示出发点到山顶的路程)?
目标导学:一元一次不等式的应用
前面问题中涉及的数量关系是:
去时所花时间+休息时间+回来所花时间≤总时间.
解:设从出发点到山顶的距离为x km,
则他们去时所花时间为 h,回来所花时间为 h.
他们在山顶休息了2 h,又上午7点到下午4点之间总共相隔9 h,即所用时间应小于或等于9 h.
所以有 +2+ ≤ 9.
解得 x≤12.
因此要满足下午4点以前必须返回出发点,小华他们最远能登上D山顶.
梳理归纳
列一元一 次方程解决实际问题(包含等量关系)
(1)审:审题、找等量关系
(2)设:设未知数
(3)列:列方程
(4)解:解方程
(5)答:根据实际情况作答
列一元一次不等式解决实际问题
(包含不等关系)
(1)审:审题、找不等关系;
( 抓住关键词)
(5)答:根据实际情况作答
(4)解:解不等式
(2)设:设未知数;(去掉限定词)
(3)列:列不等式
常用关键词:大于、多于、超过、少于、低于、至少等。
解:由方程的解的定义,把x=3代入ax+12=0中,
得 a=-4.
把a=-4代入(a+2)x>-6中,
得-2x>-6,
解得x<3.
在数轴上表示如图:
其中正整数解有1和2.
例1.已知方程ax+12=0的解是x=3,求关于x不等式(a+2)x>-6的解集,并在数轴上表示出来,其中正整数解有哪些?
方法总结:求不等式的特殊解,先要准确求出不等式的解集,然后确定特殊解.在确定特殊解时,一定要注意是否包括端点的值,一般可以结合数轴,形象直观,一目了然.
-1
0
1
2
3
4
5
6
-1
0
1
2
3
4
5
6
例2.一个工程规定要在6天完成300方土的任务,第一天完成了60方土,现要比原计划至少提前2天完成任务,那么以后平均每天至少要完成多少方土?
解:设以后平均每天至少要完成x方土,
则有:60+(6-1-2)x≥300,
解得:x≥80,
即以后平均每天至少要完成80方土.
例3.在一次知识竞赛中,有10道抢答题,答对一题得10分,答错一题扣5分,不答得0分,小玲一道题没有答,成绩仍然不低于60分,她至少答对几道题?
解:设小玲答对的题数是x道,则答错的题数是
(9-x)道,根据题意,得
10x-5(9-x) ≥60
解这个不等式,得 x ≥ 7
答:她至少答对7道题。
思考:小玲有几种答题可能?
分析:答对题得的分数 — 答错题扣的分数 ≥ 60分
例4.某城市的出租车的起价是10元(即行驶路程在5千米以内都需要付10元),达到或超过5千米后,每增加1千米加价1.2元(不足1千米按1千米算),现在某人乘这种出租车从甲地到乙地,支付车费17.2元,从甲地到乙地的路程最多是多少千米
解:设从甲地到乙地的路程是x千米.
10+1.2(x- 5)≤17.2,
解得x≤11.
因此从甲地到乙地的路程最多是11千米.
为了举行班级晚会,孔明准备去商店购买20个乒乓球做道具,并买一些乒乓球拍做奖品.已知乒乓球每个1.5元,球拍每个22元.如果购买金额不超过200元,且买的球拍尽可能多,那么孔明应该买多少个球拍
解:设孔明购买x个乒乓球拍,则购买球拍需要22x元,买20个乒乓球做道具需要(1.5×20)元.
因为购买金额不超过200元, 所以22x+1.5×20≤200.
解得x≤ 因为x为正整数,且x取最大值,所以x=7.
答:要买的球拍尽可能多,那么孔明应该买7个球拍.
练一练
应用一元一次不等式解决实际问题的步骤:
实际问题
解不等式
列不等式
结合实际
确定答案
找出不等关系
设未知数
课堂小结
1、如图所示,小明和爸爸、妈妈三人玩跷跷板.三人的体重一共为150千克,爸爸坐在跷跷板的一端,体重只有妈妈一半的小明和妈妈一同坐在跷跷板的另一端,这时爸爸那端仍然着地.那么小明的体重应小于( )
A.49千克
B.50千克
C.24千克
D.25千克
D
检测目标
2.某射箭运动员在一次比赛中,前6次射击共击中52环,如果他要打破89环(10次射击,每次射击最高中10环)的记录,则他第7次射击不能少于( )
A.6环 B.7环 C.8环 D.9环
C
检测目标
设需要购买x块地板砖,则有
5×4≤0.6×0.6x
解得 x ≥ 55.6
由于地板砖的数目必须是整数,所以x的最小值为56.
答:小明至少要购买56块地板砖.
解:
3.小明家的客厅长5 m,宽4 m.现在想购买边长为60 cm的正方形地板砖把地面铺满,至少需要购买多少块这样的地板砖?
检测目标
4.某市打市内电话的收费标准是:每次3 min以内(含3 min)0.22元,以后每分钟0.11元(不足1 min部分按1 min计).小琴一天在家里给同学打了一次市内电话,所用电话费没超过0.5元.她最多打了几分钟的电话?
解:设小琴打了x分钟的电话,则有
0.22+ (x-3) ×0.11≤0.5
解得 x ≤5.5
由于电话计时按照分钟计时,x应是整数,所以x的最大值为5.
答:小琴最多打了5min的电话.
检测目标
通过本课学习,你收获了什么?
1、解一元一次不等式的一般步骤:
(1)去分母;
(2)去括号;
(3)移项;
(4)合并同类项;
(5)系数化为1.(注意不等号的方向)
知识回顾
2、列一元一次方程解决实际问题的一般步骤:
(1)审:审题,找等量关系;
(2)设:设未知数;
(3)列:列方程;
(4)解:解方程;
(5)答:根据实际情况作答.
9.2 一元一次不等式
第2课时 一元一次不等式的应用
人教版七年级数学 下册
目标导航
1.会通过列一元一次不等式去解决生活中的实际问 题,经历“实际问题抽象为不等式模型”的过程;(重点)
2.体会解不等式过程中的化归思想与类比思想,体会分类讨论思想在用不等式解决实际问题中的应用.
小华打算在星期天与同学去登山,计划上午7点出发,到达山顶后休息2h,下午4点以前必须回到出发点. 如果他们去时的平均速度是3km/h,回来时的平均速度是4km/h,他们最远能登上哪座山顶(图中数字表示出发点到山顶的路程)?
目标导学:一元一次不等式的应用
前面问题中涉及的数量关系是:
去时所花时间+休息时间+回来所花时间≤总时间.
解:设从出发点到山顶的距离为x km,
则他们去时所花时间为 h,回来所花时间为 h.
他们在山顶休息了2 h,又上午7点到下午4点之间总共相隔9 h,即所用时间应小于或等于9 h.
所以有 +2+ ≤ 9.
解得 x≤12.
因此要满足下午4点以前必须返回出发点,小华他们最远能登上D山顶.
梳理归纳
列一元一 次方程解决实际问题(包含等量关系)
(1)审:审题、找等量关系
(2)设:设未知数
(3)列:列方程
(4)解:解方程
(5)答:根据实际情况作答
列一元一次不等式解决实际问题
(包含不等关系)
(1)审:审题、找不等关系;
( 抓住关键词)
(5)答:根据实际情况作答
(4)解:解不等式
(2)设:设未知数;(去掉限定词)
(3)列:列不等式
常用关键词:大于、多于、超过、少于、低于、至少等。
解:由方程的解的定义,把x=3代入ax+12=0中,
得 a=-4.
把a=-4代入(a+2)x>-6中,
得-2x>-6,
解得x<3.
在数轴上表示如图:
其中正整数解有1和2.
例1.已知方程ax+12=0的解是x=3,求关于x不等式(a+2)x>-6的解集,并在数轴上表示出来,其中正整数解有哪些?
方法总结:求不等式的特殊解,先要准确求出不等式的解集,然后确定特殊解.在确定特殊解时,一定要注意是否包括端点的值,一般可以结合数轴,形象直观,一目了然.
-1
0
1
2
3
4
5
6
-1
0
1
2
3
4
5
6
例2.一个工程规定要在6天完成300方土的任务,第一天完成了60方土,现要比原计划至少提前2天完成任务,那么以后平均每天至少要完成多少方土?
解:设以后平均每天至少要完成x方土,
则有:60+(6-1-2)x≥300,
解得:x≥80,
即以后平均每天至少要完成80方土.
例3.在一次知识竞赛中,有10道抢答题,答对一题得10分,答错一题扣5分,不答得0分,小玲一道题没有答,成绩仍然不低于60分,她至少答对几道题?
解:设小玲答对的题数是x道,则答错的题数是
(9-x)道,根据题意,得
10x-5(9-x) ≥60
解这个不等式,得 x ≥ 7
答:她至少答对7道题。
思考:小玲有几种答题可能?
分析:答对题得的分数 — 答错题扣的分数 ≥ 60分
例4.某城市的出租车的起价是10元(即行驶路程在5千米以内都需要付10元),达到或超过5千米后,每增加1千米加价1.2元(不足1千米按1千米算),现在某人乘这种出租车从甲地到乙地,支付车费17.2元,从甲地到乙地的路程最多是多少千米
解:设从甲地到乙地的路程是x千米.
10+1.2(x- 5)≤17.2,
解得x≤11.
因此从甲地到乙地的路程最多是11千米.
为了举行班级晚会,孔明准备去商店购买20个乒乓球做道具,并买一些乒乓球拍做奖品.已知乒乓球每个1.5元,球拍每个22元.如果购买金额不超过200元,且买的球拍尽可能多,那么孔明应该买多少个球拍
解:设孔明购买x个乒乓球拍,则购买球拍需要22x元,买20个乒乓球做道具需要(1.5×20)元.
因为购买金额不超过200元, 所以22x+1.5×20≤200.
解得x≤ 因为x为正整数,且x取最大值,所以x=7.
答:要买的球拍尽可能多,那么孔明应该买7个球拍.
练一练
应用一元一次不等式解决实际问题的步骤:
实际问题
解不等式
列不等式
结合实际
确定答案
找出不等关系
设未知数
课堂小结
1、如图所示,小明和爸爸、妈妈三人玩跷跷板.三人的体重一共为150千克,爸爸坐在跷跷板的一端,体重只有妈妈一半的小明和妈妈一同坐在跷跷板的另一端,这时爸爸那端仍然着地.那么小明的体重应小于( )
A.49千克
B.50千克
C.24千克
D.25千克
D
检测目标
2.某射箭运动员在一次比赛中,前6次射击共击中52环,如果他要打破89环(10次射击,每次射击最高中10环)的记录,则他第7次射击不能少于( )
A.6环 B.7环 C.8环 D.9环
C
检测目标
设需要购买x块地板砖,则有
5×4≤0.6×0.6x
解得 x ≥ 55.6
由于地板砖的数目必须是整数,所以x的最小值为56.
答:小明至少要购买56块地板砖.
解:
3.小明家的客厅长5 m,宽4 m.现在想购买边长为60 cm的正方形地板砖把地面铺满,至少需要购买多少块这样的地板砖?
检测目标
4.某市打市内电话的收费标准是:每次3 min以内(含3 min)0.22元,以后每分钟0.11元(不足1 min部分按1 min计).小琴一天在家里给同学打了一次市内电话,所用电话费没超过0.5元.她最多打了几分钟的电话?
解:设小琴打了x分钟的电话,则有
0.22+ (x-3) ×0.11≤0.5
解得 x ≤5.5
由于电话计时按照分钟计时,x应是整数,所以x的最大值为5.
答:小琴最多打了5min的电话.
检测目标
通过本课学习,你收获了什么?
