人教版七年级数学 下册 9.3 一元一次不等式组 课件(共33张PPT)
文档属性
| 名称 | 人教版七年级数学 下册 9.3 一元一次不等式组 课件(共33张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-30 15:51:21 | ||
图片预览










文档简介
(共33张PPT)
解一元一次不等式的基本步骤
1、去分母 (不等式的性质2)
2、去括号 (乘法分配律)
3、移项 (不等式的性质1)
4、合并同类项 (整式加减性质)
5、化系数为1 (不等式性质2,3)
知识回顾
同学们,你能根据上图对话片断估计出这头大象的体重范围吗 请说说你的理由!
若设大象的体重为X吨,请用不等式的知识分别表示上面两位同学所谈话的内容:
②
①
类似于方程组,把这两个一元一次不等式合起来,组成一个一元一次不等式组
看,这头大象好大呀,体重肯定大于3吨!
嗨,我听管理员说,这头大象的体重不足5吨呢!
9.3 一元一次不等式组
人教版七年级数学 下册
目标导航
1.掌握一元一次不等式组概念及解法。
2.形成正确的解不等式组的思路与方法;(重点、难点)
3.掌握在数轴上正确表示一元一次不等式组的解集的方法。
问题:一个长方形足球场的宽为70m,如果它的周长大于350m,面积小于7630m2,求这个足球场的长的取值范围,并判断这个足球场是否可以进行国际足球比赛
(注:用于国际足球比赛的足球场的长在100至110m之间,宽在64至75m之间).
目标导学一:一元一次不等式组的概念及解集
如果设足球场的长为x m,那么它的周长就是2(x+70)m,面积为70x m2.
根据已知条件,我们知道x的取值范围要使
2(x+70)>350 和70x<7630
这两个不等式同时成立.
为此,我们用大括号把上述两个不等式联立起来,得
2(x+70)>350 和70x<7630
像 这样,关于同一未知数的两个一元一次不等式合在一起,就组成一个一元一次不等式组.
下列各不等式组,其中是一元一次不等式组的有________.(填序号)
① ② ③
④ ⑤ ⑥
练习:
③④⑤
如何判定一个不等式组是一元一次不等式组?
(1)不等式组中只含有一个未知数;
(2)组成不等式组的每个不等式必须是一元一次不等式.
思考:
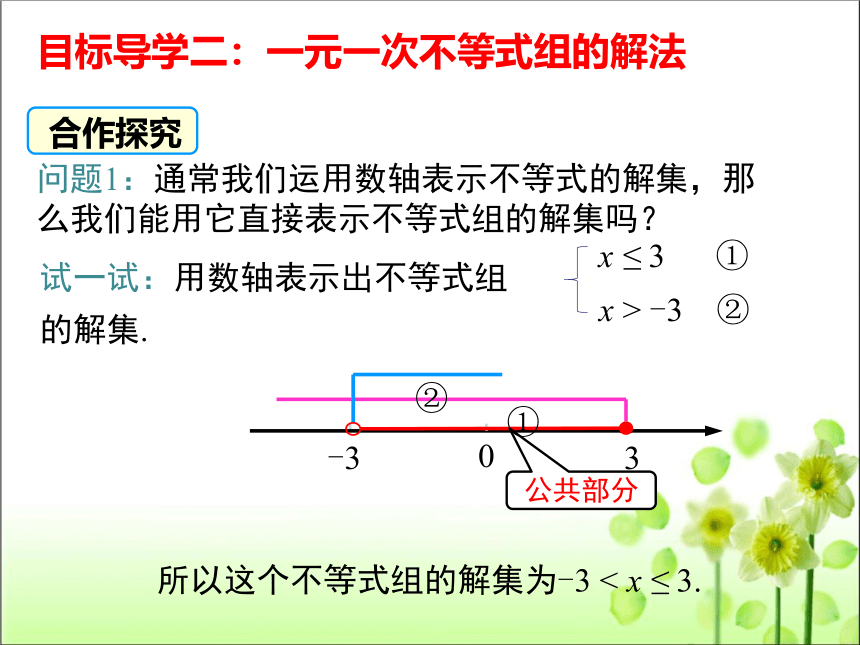
问题1:通常我们运用数轴表示不等式的解集,那么我们能用它直接表示不等式组的解集吗?
试一试:用数轴表示出不等式组 的解集.
所以这个不等式组的解集为-3 < x ≤ 3.
x > -3 ②
x ≤ 3 ①
0
-3
3
公共部分
①
②
合作探究
目标导学二:一元一次不等式组的解法
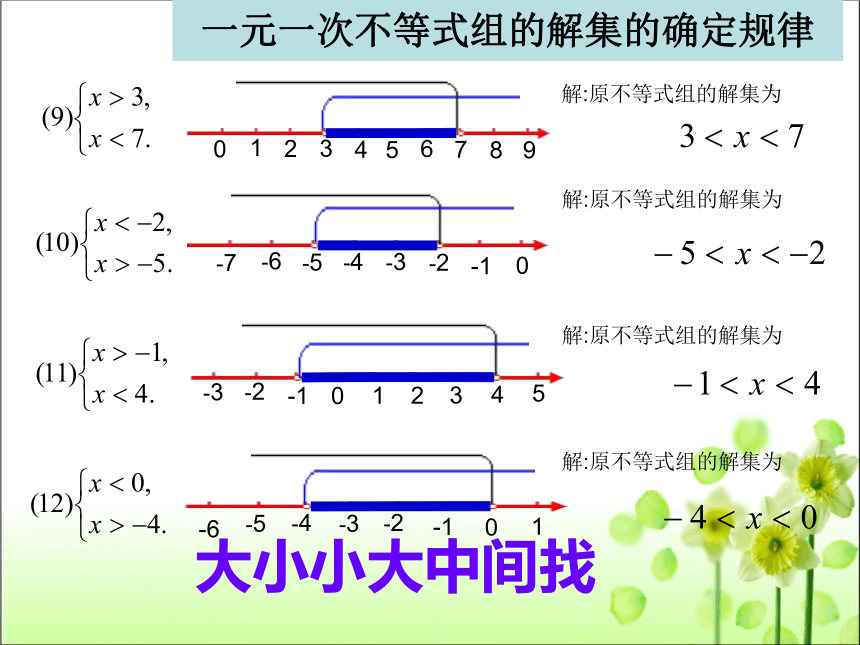
一元一次不等式组的解集的确定规律
学生活动
-5
-2
0
-3
-1
-4
0
7
6
5
4
2
1
3
8
9
-3
-2
-1
0
4
2
1
3
-5
-2
0
-3
-1
2
1
-4
解:原不等式组的解集为
解:原不等式组的解集为
解:原不等式组的解集为
解:原不等式组的解集为
大大取大
-5
-2
0
-3
-1
1
-4
-6
-3
-2
-1
0
4
2
1
3
5
-5
-2
-3
-1
-4
0
-7
-6
0
7
6
5
4
2
1
3
8
9
解:原不等式组的解集为
解:原不等式组的解集为
解:原不等式组的解集为
解:原不等式组的解集为
小小取小
一元一次不等式组的解集的确定规律
-5
-2
0
-3
-1
1
-4
-6
-5
-2
-3
-1
-4
0
-7
-6
0
7
6
5
4
2
1
3
8
9
-3
-2
-1
0
4
2
1
3
5
解:原不等式组的解集为
解:原不等式组的解集为
解:原不等式组的解集为
解:原不等式组的解集为
大小小大中间找
一元一次不等式组的解集的确定规律
0
7
6
5
4
2
1
3
8
9
-5
-2
-3
-1
-4
0
-7
-6
-3
-2
-1
0
4
2
1
3
5
-5
-2
0
-3
-1
1
-4
-6
解:原不等式组无解.
解:原不等式组无解.
解:原不等式组无解.
解:原不等式组无解.
大大小小无解了
一元一次不等式组的解集的确定规律
观察下面四个不等式组,并利用数轴写出下列不等式组的解集.
(
(
(
(
解不等式②,得
x <-3.
例1 解不等式组:
解: 解不等式①,得
x ≤ 3.
①
②
把不等式①、②的解集在数轴上表示出来,如图:
0
-3
3
由图可知,不等式①、②的解集的公共部分就是
x<-3,所以这个不等式组的解集是 x<-3.
典例精析
解一元一次不等式组的一般步骤:
(1)分别解每一个不等式;
(2)利用数轴法确定不等式组的解集;
(3)写出不等式组的解集.
例2 解不等式组:
①
②
解: 解不等式①,得
x >-2.
解不等式②,得
x >6.
把不等式①、②的解集在数轴上表示出来,
如图:
0
-2
6
由图可知,不等式①、②的解集的公共部分就是x>6,所以这个不等式组的解集是x>6.
例3.不等式组 的解集为x<4,求a的取值范围.
五、巩固练习
x-a<0,
3x+2>5x-6
解:
解不等式①得x<a.
解不等式②得x<4.
因为此不等式组的解集为x<4,所以a≥4.
x-a<0, ①
3x+2>5x-6. ②
例4 已知不等式组 的解集为-1<x<1,
则(a+1)(b-1)的值为多少
2x—a<1
x—2b>3
解: 由不等式组得:
x <
x >3+2b
因为不等式组的解集为: -1< x < 1 ,
所以,
=1
3+2b= -1
解得 a=1 , b= - 2
所以(a+1)(b-1)=2×(-3)=-6
解不等式①得:
x> 2
解不等式②得:
x≥3
在数轴上表示不等式①、②的解集:
解不等式组,并在数轴上表示不等式组的解集.
解:
2
3
0
从图中可以找出不等式解集的公共部分,
所以不等式组的解集为:
x≥3
同大取大
练一练
从图中可以看到不等式解集没有公共部分,
所以,这个不等式组无解.
解:解不等式①,得
解不等式②,得
①
②
(2)
在数轴上表示不等式①、②的解集:
0
8
大大小小无解
例5. 3个小组计划在10天内生产500件产品(每天生产量相同),按原先的生产速度,不能完成任务;如果每个小组每天比原先多生产1件产品,就能提前完成任务.每个小组原先每天生产多少件产品?
目标导学三:一元一次不等式组的应用
解:设每个小组原先每天生产x件产品,由题意,得
3×10x<500,
3×10(x+1)>500
解不等式组,得
根据题意,x的值应是整数,所以x=16.
答:每个小组原先每天生产16件产品.
因为x只能取整数,所以x=6,即有6辆汽车运这批货物.
例6 用若干辆载重量为 8 t 的汽车运一批货物,若每辆汽车只装 4 t ,则剩下 20 t 货物;若每辆汽车装满 8 t,则最后一辆汽车不满也不空.请你算一算:有多少辆汽车运这批货物?
解:设有x 辆汽车,则这批货物共有(4x+20 )t.依题意得
解不等式组,得5<x <7.
四、运用新知
解:解不等式组
得 <x≤4.
所以x可取的整数值是-2,-1,0,1,2,3,4.
5x+2>3(x-1),
≤
练一练 x取哪些整数时,不等式5x+2>3(x-1)与 都成立
≤
1.一元一次不等式组的基本概念:
(1)一元一次不等式组的定义;
(2)一元一次不等式组的解集;
(3)解一元一次不等式组.
2.解一元一次不等式组的一般步骤:
(1)分别解每一个不等式;
(2)利用数轴法确定不等式组的解集;
(3)写出不等式组的解集.
课堂小结
3+x <4+2x
5x-3<4x-1
7+2x>6+3x
{
(5)
1、下列不等式组中哪些是一元一次不等式组?
(否)
(是)
(否)
(是)
(是)
注 意
一元一次不等式组中各不等式所含未知数必须相同且代表同一个量
检测目标
解法探究
2、利用数轴来确定不等式组的解集:
x >3
x >-1
(1)
∴不等式组的解集是: x >3
x < 3
x <-1
(2)
∴不等式组的解集是: x <-1
x < 3
x >-1
(3)
∴不等式组的解集是: -1< x <3
x > 3
x <-1
(4)
3
-1
3
-1
3
-1
3
-1
∴不等式组的解集是: 无解
检测目标
3、不等式组
的正整数解是( )
A.0和1 B.2和3 C.1和3 D.1和2
D
检测目标
4、解下列不等式组:
(1) (2)
(3)
2x>1-x,
x+2<4x-1;
x-5>1+2x,
3x+2≤4x;
+5>1-x,
x-1≤ .
(1)x>1
(2)空集
(3)
检测目标
5.把一篮苹果分给几个学生,若每人分4个,则剩余
3个;若每人分6个,则最后一个学生最多分2个,
求学生人数和苹果分别是多少?
解:设学生有x个,则苹果有(4x+3)个,根据题意,得
(4x+3)-6(x-1)>0,
(4x+3)-6(x-1)≤2.
解不等式组,得3.5≤x<4.5
根据题意,x的值应是整数,所以x=4,则4x+3=19.
答:学生有4人,苹果有19个.
通过本课学习,你收获了什么?
解一元一次不等式的基本步骤
1、去分母 (不等式的性质2)
2、去括号 (乘法分配律)
3、移项 (不等式的性质1)
4、合并同类项 (整式加减性质)
5、化系数为1 (不等式性质2,3)
知识回顾
同学们,你能根据上图对话片断估计出这头大象的体重范围吗 请说说你的理由!
若设大象的体重为X吨,请用不等式的知识分别表示上面两位同学所谈话的内容:
②
①
类似于方程组,把这两个一元一次不等式合起来,组成一个一元一次不等式组
看,这头大象好大呀,体重肯定大于3吨!
嗨,我听管理员说,这头大象的体重不足5吨呢!
9.3 一元一次不等式组
人教版七年级数学 下册
目标导航
1.掌握一元一次不等式组概念及解法。
2.形成正确的解不等式组的思路与方法;(重点、难点)
3.掌握在数轴上正确表示一元一次不等式组的解集的方法。
问题:一个长方形足球场的宽为70m,如果它的周长大于350m,面积小于7630m2,求这个足球场的长的取值范围,并判断这个足球场是否可以进行国际足球比赛
(注:用于国际足球比赛的足球场的长在100至110m之间,宽在64至75m之间).
目标导学一:一元一次不等式组的概念及解集
如果设足球场的长为x m,那么它的周长就是2(x+70)m,面积为70x m2.
根据已知条件,我们知道x的取值范围要使
2(x+70)>350 和70x<7630
这两个不等式同时成立.
为此,我们用大括号把上述两个不等式联立起来,得
2(x+70)>350 和70x<7630
像 这样,关于同一未知数的两个一元一次不等式合在一起,就组成一个一元一次不等式组.
下列各不等式组,其中是一元一次不等式组的有________.(填序号)
① ② ③
④ ⑤ ⑥
练习:
③④⑤
如何判定一个不等式组是一元一次不等式组?
(1)不等式组中只含有一个未知数;
(2)组成不等式组的每个不等式必须是一元一次不等式.
思考:
问题1:通常我们运用数轴表示不等式的解集,那么我们能用它直接表示不等式组的解集吗?
试一试:用数轴表示出不等式组 的解集.
所以这个不等式组的解集为-3 < x ≤ 3.
x > -3 ②
x ≤ 3 ①
0
-3
3
公共部分
①
②
合作探究
目标导学二:一元一次不等式组的解法
一元一次不等式组的解集的确定规律
学生活动
-5
-2
0
-3
-1
-4
0
7
6
5
4
2
1
3
8
9
-3
-2
-1
0
4
2
1
3
-5
-2
0
-3
-1
2
1
-4
解:原不等式组的解集为
解:原不等式组的解集为
解:原不等式组的解集为
解:原不等式组的解集为
大大取大
-5
-2
0
-3
-1
1
-4
-6
-3
-2
-1
0
4
2
1
3
5
-5
-2
-3
-1
-4
0
-7
-6
0
7
6
5
4
2
1
3
8
9
解:原不等式组的解集为
解:原不等式组的解集为
解:原不等式组的解集为
解:原不等式组的解集为
小小取小
一元一次不等式组的解集的确定规律
-5
-2
0
-3
-1
1
-4
-6
-5
-2
-3
-1
-4
0
-7
-6
0
7
6
5
4
2
1
3
8
9
-3
-2
-1
0
4
2
1
3
5
解:原不等式组的解集为
解:原不等式组的解集为
解:原不等式组的解集为
解:原不等式组的解集为
大小小大中间找
一元一次不等式组的解集的确定规律
0
7
6
5
4
2
1
3
8
9
-5
-2
-3
-1
-4
0
-7
-6
-3
-2
-1
0
4
2
1
3
5
-5
-2
0
-3
-1
1
-4
-6
解:原不等式组无解.
解:原不等式组无解.
解:原不等式组无解.
解:原不等式组无解.
大大小小无解了
一元一次不等式组的解集的确定规律
观察下面四个不等式组,并利用数轴写出下列不等式组的解集.
(
(
(
(
解不等式②,得
x <-3.
例1 解不等式组:
解: 解不等式①,得
x ≤ 3.
①
②
把不等式①、②的解集在数轴上表示出来,如图:
0
-3
3
由图可知,不等式①、②的解集的公共部分就是
x<-3,所以这个不等式组的解集是 x<-3.
典例精析
解一元一次不等式组的一般步骤:
(1)分别解每一个不等式;
(2)利用数轴法确定不等式组的解集;
(3)写出不等式组的解集.
例2 解不等式组:
①
②
解: 解不等式①,得
x >-2.
解不等式②,得
x >6.
把不等式①、②的解集在数轴上表示出来,
如图:
0
-2
6
由图可知,不等式①、②的解集的公共部分就是x>6,所以这个不等式组的解集是x>6.
例3.不等式组 的解集为x<4,求a的取值范围.
五、巩固练习
x-a<0,
3x+2>5x-6
解:
解不等式①得x<a.
解不等式②得x<4.
因为此不等式组的解集为x<4,所以a≥4.
x-a<0, ①
3x+2>5x-6. ②
例4 已知不等式组 的解集为-1<x<1,
则(a+1)(b-1)的值为多少
2x—a<1
x—2b>3
解: 由不等式组得:
x <
x >3+2b
因为不等式组的解集为: -1< x < 1 ,
所以,
=1
3+2b= -1
解得 a=1 , b= - 2
所以(a+1)(b-1)=2×(-3)=-6
解不等式①得:
x> 2
解不等式②得:
x≥3
在数轴上表示不等式①、②的解集:
解不等式组,并在数轴上表示不等式组的解集.
解:
2
3
0
从图中可以找出不等式解集的公共部分,
所以不等式组的解集为:
x≥3
同大取大
练一练
从图中可以看到不等式解集没有公共部分,
所以,这个不等式组无解.
解:解不等式①,得
解不等式②,得
①
②
(2)
在数轴上表示不等式①、②的解集:
0
8
大大小小无解
例5. 3个小组计划在10天内生产500件产品(每天生产量相同),按原先的生产速度,不能完成任务;如果每个小组每天比原先多生产1件产品,就能提前完成任务.每个小组原先每天生产多少件产品?
目标导学三:一元一次不等式组的应用
解:设每个小组原先每天生产x件产品,由题意,得
3×10x<500,
3×10(x+1)>500
解不等式组,得
根据题意,x的值应是整数,所以x=16.
答:每个小组原先每天生产16件产品.
因为x只能取整数,所以x=6,即有6辆汽车运这批货物.
例6 用若干辆载重量为 8 t 的汽车运一批货物,若每辆汽车只装 4 t ,则剩下 20 t 货物;若每辆汽车装满 8 t,则最后一辆汽车不满也不空.请你算一算:有多少辆汽车运这批货物?
解:设有x 辆汽车,则这批货物共有(4x+20 )t.依题意得
解不等式组,得5<x <7.
四、运用新知
解:解不等式组
得 <x≤4.
所以x可取的整数值是-2,-1,0,1,2,3,4.
5x+2>3(x-1),
≤
练一练 x取哪些整数时,不等式5x+2>3(x-1)与 都成立
≤
1.一元一次不等式组的基本概念:
(1)一元一次不等式组的定义;
(2)一元一次不等式组的解集;
(3)解一元一次不等式组.
2.解一元一次不等式组的一般步骤:
(1)分别解每一个不等式;
(2)利用数轴法确定不等式组的解集;
(3)写出不等式组的解集.
课堂小结
3+x <4+2x
5x-3<4x-1
7+2x>6+3x
{
(5)
1、下列不等式组中哪些是一元一次不等式组?
(否)
(是)
(否)
(是)
(是)
注 意
一元一次不等式组中各不等式所含未知数必须相同且代表同一个量
检测目标
解法探究
2、利用数轴来确定不等式组的解集:
x >3
x >-1
(1)
∴不等式组的解集是: x >3
x < 3
x <-1
(2)
∴不等式组的解集是: x <-1
x < 3
x >-1
(3)
∴不等式组的解集是: -1< x <3
x > 3
x <-1
(4)
3
-1
3
-1
3
-1
3
-1
∴不等式组的解集是: 无解
检测目标
3、不等式组
的正整数解是( )
A.0和1 B.2和3 C.1和3 D.1和2
D
检测目标
4、解下列不等式组:
(1) (2)
(3)
2x>1-x,
x+2<4x-1;
x-5>1+2x,
3x+2≤4x;
+5>1-x,
x-1≤ .
(1)x>1
(2)空集
(3)
检测目标
5.把一篮苹果分给几个学生,若每人分4个,则剩余
3个;若每人分6个,则最后一个学生最多分2个,
求学生人数和苹果分别是多少?
解:设学生有x个,则苹果有(4x+3)个,根据题意,得
(4x+3)-6(x-1)>0,
(4x+3)-6(x-1)≤2.
解不等式组,得3.5≤x<4.5
根据题意,x的值应是整数,所以x=4,则4x+3=19.
答:学生有4人,苹果有19个.
通过本课学习,你收获了什么?
