1.5 弹性碰撞与非弹性碰撞(共17张ppt)
文档属性
| 名称 | 1.5 弹性碰撞与非弹性碰撞(共17张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-04-29 13:42:54 | ||
图片预览






文档简介
(共17张PPT)
1.5 弹性碰撞和非弹性碰撞
碰撞是自然界中常见的现象。陨石撞击地球而对地表产生破坏,网球受球拍撞击而改变运动状态......物体碰撞中动量的变化情况,前面已进行了研究。那么,在各种碰撞中能量又是如何变化的?
1.碰撞:物体之间在很短时间内的相互作用。
2.碰撞特点:
(1)作用时间很短
(2)内力远大于外力
(3)几乎在原始位置进行
动量守恒
一、弹性碰撞和非弹性碰撞
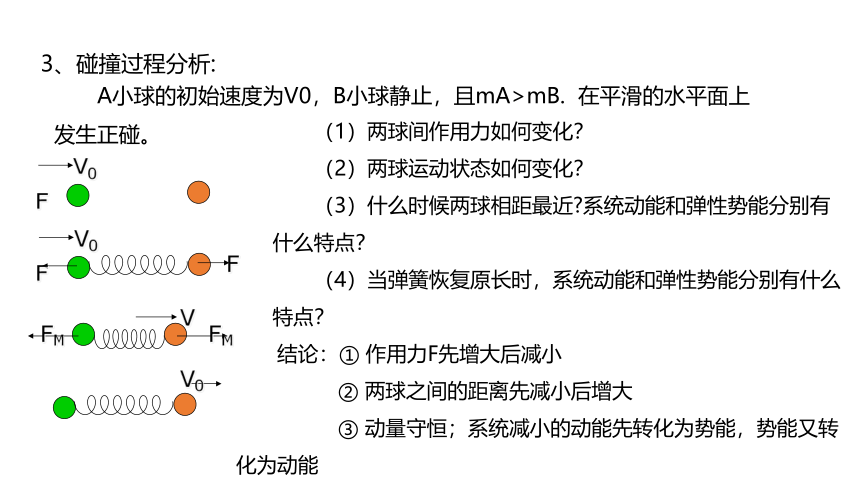
3、碰撞过程分析:
V
FM
FM
V0
F
F
V0
结论:① 作用力F先增大后减小
② 两球之间的距离先减小后增大
③ 动量守恒;系统减小的动能先转化为势能,势能又转 化为动能
A小球的初始速度为V0,B小球静止,且mA>mB. 在平滑的水平面上发生正碰。
(1)两球间作用力如何变化?
(2)两球运动状态如何变化?
(3)什么时候两球相距最近 系统动能和弹性势能分别有 什么特点?
(4)当弹簧恢复原长时,系统动能和弹性势能分别有什么特点?
V0
F
4、碰撞的种类:
(3) 弹性碰撞:P=P ,Ek=Ek ,两球恢复原状
(2) 非弹性碰撞:P=P ,Ek>Ek ,两球无法恢复原状
(1) 完全非弹性碰撞:VA=VB ΔEK最大,两球相距最近
例:两个物体的质量为m,碰撞前一个物体静止,另一个以速度v像它撞去。碰撞后两个物体粘在一起,成为一个质量为2m的物体,并以速度v’继续向前移动。在这次碰撞中能量守恒吗?
v
静止
m
m
v’
2m
根据动量守恒定律
碰撞后的共同速度
碰撞前的总动能
碰撞后的总动能
不守恒
1.冰球运动员甲的体重为80.0kg。当他以5.0m/s的速度向前运动时,他与另一名体重100kg、速度为3.0m/s的迎面而来的运动员乙相撞。相撞后甲恰好静止。假设碰撞时间很短,求:
(1)碰撞后乙的速度的大小;
(2)碰撞中总机械能的损失。
1.0 m/s
1400J
属于非弹性碰撞和完全非弹性碰撞
思考:如果两个球在碰撞后粘在一起,则每个球的速度分别多少?动能的损失是多少? 一、两次分别属于什么碰撞?
一维弹性碰撞后速度的确定
v1
v1/
m1
v2/
m2
m1
m2
二、弹性碰撞的实例分析:
2.在光滑水平面上有A、B两球,其质量分别为mA和mB,两个球在t0时发生碰撞,碰撞过程中没有机械能损失,两球在碰撞前后的速度-时间如图所示,则下列关系式正确的是( )
A.mA>mB B.mAC.mA=mB D.无法判断
拓展:
画出mA=mB;mA>mB这两种情况下A、B的v-t图象
理解记忆
B
④若 m1②若 m1 >m2 , 则 大撞小,同向跑 (如运动钢球碰撞静止玻璃球)
①若 m1 = m2,则 等质量物体弹性碰撞速度交换(如打台球)
弹性碰撞(机械能守恒)——“一动一静模型”
③若 m1 >m2 , 则
⑤若 m1碰撞过程中系统动量守恒
弹性碰撞中没有机械能损失
若v2=0时,结论与前面的是否相同?
如果在光滑的水平面上有两个质量为m1和m2的刚性球A和B,它们以初始速度v1、v2运动,若它们能发生碰撞(为一维弹性碰撞),碰撞后它们的速度v1'和v2'分别是多少?
思考讨论
3.两个球A、B在平滑的水平面上沿相同的直线和方向运动,mA=1kg,mB=2kg,vA=6米m/s,vB=2m/s, 当球A追上B并碰撞后,两个球A和B的速度的可能值为(以两球碰撞前的运动方向为正)( )
A.vA′=5 m/s,vB′=2.5 m/s
B.vA′=2 m/s,vB′=4 m/s
C.vA′=-4 m/s,vB′=7 m/s
D.vA′=7 m/s,vB′= 1.5 m/s
///////////////////////
A
B
1.碰撞前后动量守恒:P=mAvA+mBvB=10kg.m/s
2.如碰撞后向同方向运动,则后面物体的速度不能大于前面物体的速度.即碰撞后:A的速度减小,或反向,B的速度增大。
3.系统的总动能不能增加
B
分析碰撞问题的关键点
(1)遵守动量守恒定律
(2)系统的动能应不增加
(3)碰撞后每个物体的运动情况要符合实际情况。
碰撞可能性判断的三个依据:
——守恒
——不增
——合理
动量制约
动能制约
运动制约
1.(选择题)在一个光滑的水平面上,两球沿球心的连线以相等的速率相向而行,并发生碰撞,则以下现象可能是( )
A.若两球质量相同,碰撞后以某一相等的速率相互分开
B.若两球质量相同,碰撞后以某一相等的速率同向而行
C.若两球质量不同,碰撞后以某一相等速率相互分开
D.若两球质量不同,碰撞后以某一相等速率同向而行
解析:碰撞前、后两小球组成的系统总动量守恒。碰撞前和碰撞后的总动量为零,因此选项A是可能的;如果两个球在碰撞后以某一相等的速率同向而行,那么两个球的总动量不为零,因此选项B是不可能的;碰撞前、后系统的总动量方向不同,所以动量不守恒,选项C是不可能的;碰撞前、后的总动量不为零,方向可能是相同的,因此,选项D是可能的。
AD
2.如图所示,在光滑的水平面上,使用相等且相反的F1、F2同时作用于两个静止物体A、B上,已知mAA.静止 B.向右移动
C.向左移动 D.无法确定
解析:选取A、B两个物体组成的系统作为研究对象,在整个运动过程中,系统所受的合外力为零,所以动量改变量为零。初始时刻系统是静止的,总动量为零,最后粘合体的动量为零,即粘合体静止,所以选项A正确。
A
3.沙堆上有一块木块,质量Mo=5kg,木块上放一个爆竹,质量M=0.10kg。点燃爆竹后,木块落入5cm深沙中。若沙对木块运动的阻力始终为58 N,则不考虑爆竹中的火药质量和空气阻力。找出爆竹上升的最大高度。(g取10 m/s )
解析:火药爆炸时内力远大于重力,所以爆炸时动量守恒,设v、v'分别为爆炸后爆竹和木块的速率,取向上的方向分别为正方向,
由动量守恒定律得mv-m0v'=0①
木块落入沙中,做匀减速运动到停止,其加速度为
木块做匀减速运动的初速度
②代入①式,得v=20 m/s
爆竹以初速度v做竖直上抛运动,上升的最大高度为
课堂总结
弹性碰撞和非弹性碰撞
弹性碰撞
非弹性碰撞
碰撞发生的原则
1.5 弹性碰撞和非弹性碰撞
碰撞是自然界中常见的现象。陨石撞击地球而对地表产生破坏,网球受球拍撞击而改变运动状态......物体碰撞中动量的变化情况,前面已进行了研究。那么,在各种碰撞中能量又是如何变化的?
1.碰撞:物体之间在很短时间内的相互作用。
2.碰撞特点:
(1)作用时间很短
(2)内力远大于外力
(3)几乎在原始位置进行
动量守恒
一、弹性碰撞和非弹性碰撞
3、碰撞过程分析:
V
FM
FM
V0
F
F
V0
结论:① 作用力F先增大后减小
② 两球之间的距离先减小后增大
③ 动量守恒;系统减小的动能先转化为势能,势能又转 化为动能
A小球的初始速度为V0,B小球静止,且mA>mB. 在平滑的水平面上发生正碰。
(1)两球间作用力如何变化?
(2)两球运动状态如何变化?
(3)什么时候两球相距最近 系统动能和弹性势能分别有 什么特点?
(4)当弹簧恢复原长时,系统动能和弹性势能分别有什么特点?
V0
F
4、碰撞的种类:
(3) 弹性碰撞:P=P ,Ek=Ek ,两球恢复原状
(2) 非弹性碰撞:P=P ,Ek>Ek ,两球无法恢复原状
(1) 完全非弹性碰撞:VA=VB ΔEK最大,两球相距最近
例:两个物体的质量为m,碰撞前一个物体静止,另一个以速度v像它撞去。碰撞后两个物体粘在一起,成为一个质量为2m的物体,并以速度v’继续向前移动。在这次碰撞中能量守恒吗?
v
静止
m
m
v’
2m
根据动量守恒定律
碰撞后的共同速度
碰撞前的总动能
碰撞后的总动能
不守恒
1.冰球运动员甲的体重为80.0kg。当他以5.0m/s的速度向前运动时,他与另一名体重100kg、速度为3.0m/s的迎面而来的运动员乙相撞。相撞后甲恰好静止。假设碰撞时间很短,求:
(1)碰撞后乙的速度的大小;
(2)碰撞中总机械能的损失。
1.0 m/s
1400J
属于非弹性碰撞和完全非弹性碰撞
思考:如果两个球在碰撞后粘在一起,则每个球的速度分别多少?动能的损失是多少? 一、两次分别属于什么碰撞?
一维弹性碰撞后速度的确定
v1
v1/
m1
v2/
m2
m1
m2
二、弹性碰撞的实例分析:
2.在光滑水平面上有A、B两球,其质量分别为mA和mB,两个球在t0时发生碰撞,碰撞过程中没有机械能损失,两球在碰撞前后的速度-时间如图所示,则下列关系式正确的是( )
A.mA>mB B.mA
拓展:
画出mA=mB;mA>mB这两种情况下A、B的v-t图象
理解记忆
B
④若 m1
①若 m1 = m2,则 等质量物体弹性碰撞速度交换(如打台球)
弹性碰撞(机械能守恒)——“一动一静模型”
③若 m1 >m2 , 则
⑤若 m1
弹性碰撞中没有机械能损失
若v2=0时,结论与前面的是否相同?
如果在光滑的水平面上有两个质量为m1和m2的刚性球A和B,它们以初始速度v1、v2运动,若它们能发生碰撞(为一维弹性碰撞),碰撞后它们的速度v1'和v2'分别是多少?
思考讨论
3.两个球A、B在平滑的水平面上沿相同的直线和方向运动,mA=1kg,mB=2kg,vA=6米m/s,vB=2m/s, 当球A追上B并碰撞后,两个球A和B的速度的可能值为(以两球碰撞前的运动方向为正)( )
A.vA′=5 m/s,vB′=2.5 m/s
B.vA′=2 m/s,vB′=4 m/s
C.vA′=-4 m/s,vB′=7 m/s
D.vA′=7 m/s,vB′= 1.5 m/s
///////////////////////
A
B
1.碰撞前后动量守恒:P=mAvA+mBvB=10kg.m/s
2.如碰撞后向同方向运动,则后面物体的速度不能大于前面物体的速度.即碰撞后:A的速度减小,或反向,B的速度增大。
3.系统的总动能不能增加
B
分析碰撞问题的关键点
(1)遵守动量守恒定律
(2)系统的动能应不增加
(3)碰撞后每个物体的运动情况要符合实际情况。
碰撞可能性判断的三个依据:
——守恒
——不增
——合理
动量制约
动能制约
运动制约
1.(选择题)在一个光滑的水平面上,两球沿球心的连线以相等的速率相向而行,并发生碰撞,则以下现象可能是( )
A.若两球质量相同,碰撞后以某一相等的速率相互分开
B.若两球质量相同,碰撞后以某一相等的速率同向而行
C.若两球质量不同,碰撞后以某一相等速率相互分开
D.若两球质量不同,碰撞后以某一相等速率同向而行
解析:碰撞前、后两小球组成的系统总动量守恒。碰撞前和碰撞后的总动量为零,因此选项A是可能的;如果两个球在碰撞后以某一相等的速率同向而行,那么两个球的总动量不为零,因此选项B是不可能的;碰撞前、后系统的总动量方向不同,所以动量不守恒,选项C是不可能的;碰撞前、后的总动量不为零,方向可能是相同的,因此,选项D是可能的。
AD
2.如图所示,在光滑的水平面上,使用相等且相反的F1、F2同时作用于两个静止物体A、B上,已知mA
C.向左移动 D.无法确定
解析:选取A、B两个物体组成的系统作为研究对象,在整个运动过程中,系统所受的合外力为零,所以动量改变量为零。初始时刻系统是静止的,总动量为零,最后粘合体的动量为零,即粘合体静止,所以选项A正确。
A
3.沙堆上有一块木块,质量Mo=5kg,木块上放一个爆竹,质量M=0.10kg。点燃爆竹后,木块落入5cm深沙中。若沙对木块运动的阻力始终为58 N,则不考虑爆竹中的火药质量和空气阻力。找出爆竹上升的最大高度。(g取10 m/s )
解析:火药爆炸时内力远大于重力,所以爆炸时动量守恒,设v、v'分别为爆炸后爆竹和木块的速率,取向上的方向分别为正方向,
由动量守恒定律得mv-m0v'=0①
木块落入沙中,做匀减速运动到停止,其加速度为
木块做匀减速运动的初速度
②代入①式,得v=20 m/s
爆竹以初速度v做竖直上抛运动,上升的最大高度为
课堂总结
弹性碰撞和非弹性碰撞
弹性碰撞
非弹性碰撞
碰撞发生的原则
