2.1.1 倾斜角与斜率(导学案)
文档属性
| 名称 | 2.1.1 倾斜角与斜率(导学案) |

|
|
| 格式 | docx | ||
| 文件大小 | 604.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-29 00:00:00 | ||
图片预览


文档简介
2.1.1 倾斜角与斜率
1.在平面直角坐标系中,结合具体图形,探索确定直线位置的几何要素.
2.理解直线的倾斜角和斜率的概念.
3.掌握倾斜角和斜率之间的关系.
4.掌握过两点的直线斜率的计算公式.
重点:理解直线倾斜角和斜率的概念及其关系
难点:过两点的直线斜率的计算公式.
一、自主导学
一、直线的倾斜角
定义 当直线l与x轴相交时,以x轴为基准,x轴正向与直线l向上的方向之间所成的角α叫做直线l的倾斜角
规定 当直线l与x轴平行或重合时,规定直线l的倾斜角为0°
记法 α
图示
范围 0°≤α<180°
作用 (1)表示平面直角坐标系内一条直线的倾斜程度; (2)确定平面直角坐标系中一条直线位置的几何要素是:直线上的一个定点以及它的倾斜角,二者缺一不可
点睛:倾斜角还可以这样定义:在平面直角坐标系中,对于一条与x轴相交的直线,把x轴所在的直线绕着交点按逆时针方向旋转到和直线重合时所转过的最小正角称为这条直线的倾斜角.并规定:与x轴平行或重合的直线的倾斜角为0°.
二、直线的斜率
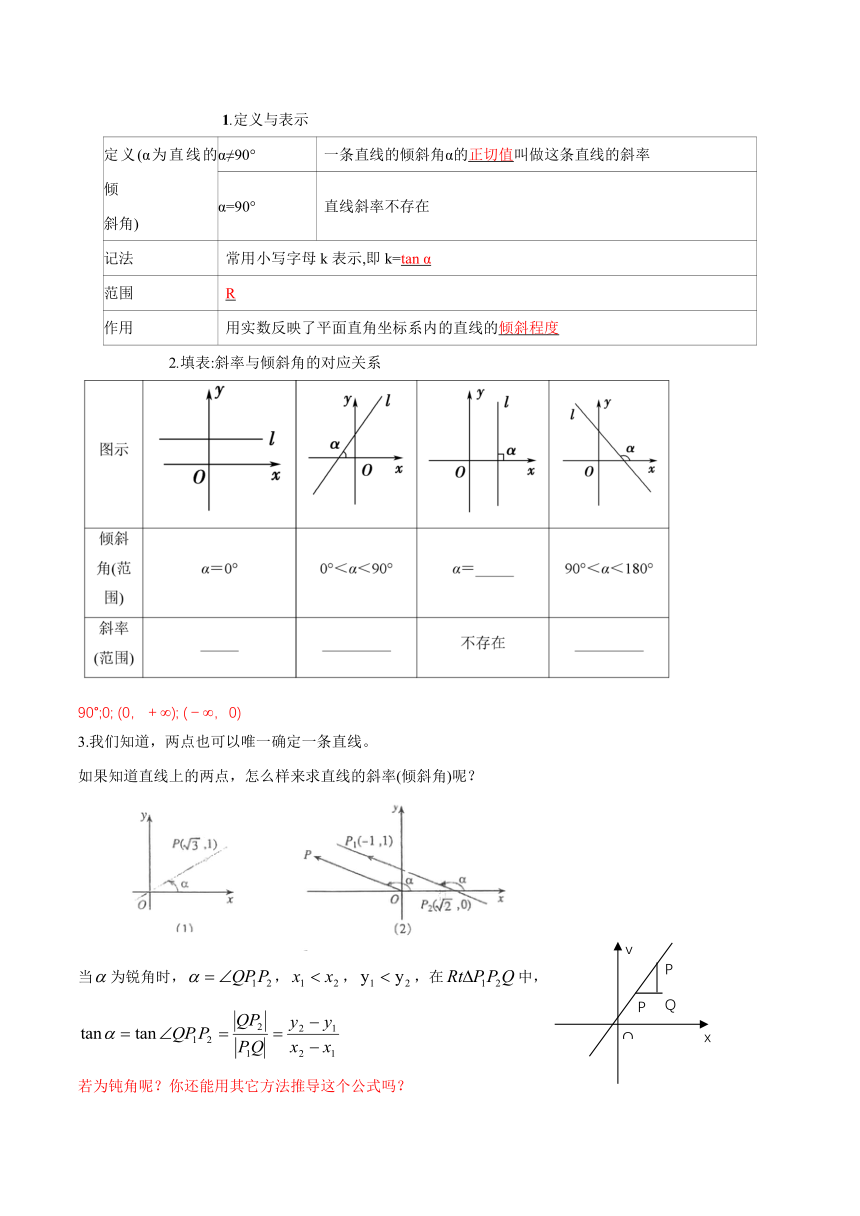
1.定义与表示
定义(α为直线的倾 斜角) α≠90° 一条直线的倾斜角α的正切值叫做这条直线的斜率
α=90° 直线斜率不存在
记法 常用小写字母k表示,即k=tan α
范围 R
作用 用实数反映了平面直角坐标系内的直线的倾斜程度
2.填表:斜率与倾斜角的对应关系
90°;0; (0,+∞); (-∞,0)
3.我们知道,两点也可以唯一确定一条直线。
如果知道直线上的两点,怎么样来求直线的斜率(倾斜角)呢?
(
y
x
P
1
xy
Oxy
P
2
·
·
Q
)
当为锐角时,,,,在中,
若为钝角呢?你还能用其它方法推导这个公式吗?
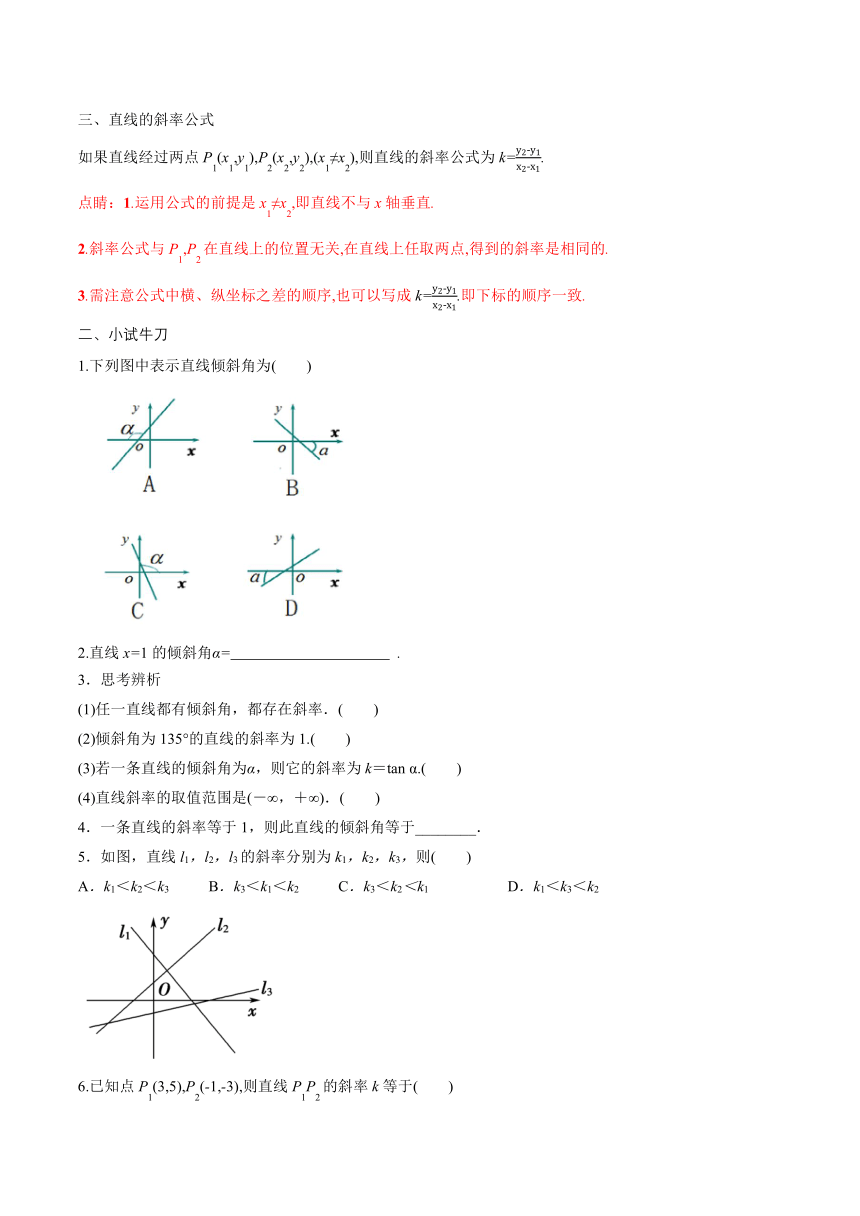
三、直线的斜率公式
如果直线经过两点P1(x1,y1),P2(x2,y2),(x1≠x2),则直线的斜率公式为k=.
点睛:1.运用公式的前提是x1≠x2,即直线不与x轴垂直.
2.斜率公式与P1,P2在直线上的位置无关,在直线上任取两点,得到的斜率是相同的.
3.需注意公式中横、纵坐标之差的顺序,也可以写成k=.即下标的顺序一致.
二、小试牛刀
1.下列图中表示直线倾斜角为( )
2.直线x=1的倾斜角α= .
3.思考辨析
(1)任一直线都有倾斜角,都存在斜率.( )
(2)倾斜角为135°的直线的斜率为1.( )
(3)若一条直线的倾斜角为α,则它的斜率为k=tan α.( )
(4)直线斜率的取值范围是(-∞,+∞).( )
4.一条直线的斜率等于1,则此直线的倾斜角等于________.
5.如图,直线l1,l2,l3的斜率分别为k1,k2,k3,则( )
A.k1<k2<k3 B.k3<k1<k2 C.k3<k2<k1 D.k1<k3<k2
6.已知点P1(3,5),P2(-1,-3),则直线P1P2的斜率k等于( )
A.2 B.1 C.D.不存在
一、情境导学
交通工程上一般用“坡度”来描述一段道路对于水平方向的倾斜程度,如图,一辆汽车沿某条道路从A点前进到B点,在水平方向前进的距离为AD,竖直方向上升的高度为DB(如果是下降,则DB的值为负实数),则坡度k=.k>0表示上坡,k<0表示下坡,为了实际应用与安全,在道路铺设时常要规划坡度的大小.那么“坡度”是如何来刻画道路的倾斜程度的呢
二、典例解析
例1 已知直线l过原点,l绕原点按顺时针方向转动角α(0°<α<180°)后,恰好与y轴重合,求直线l转动前的倾斜角是多少
直线的倾斜角的求法
求直线的倾斜角主要根据定义,其关键是根据题意画出图形,找准倾斜角,有时要根据情况分类讨论.
跟踪训练1. 设直线l过坐标原点,它的倾斜角为α,如果将l绕坐标原点按逆时针方向旋转45°,得到直线l1,那么l1的倾斜角为( )
A.α+45° B.α-135°
C.135°-α D.当0°≤α<135°时,倾斜角为α+45°;当135°≤α<180°时,倾斜角为α-135°
例2 已知直线l过点M(m+1,m-1),N(2m,1).
(1)当m为何值时,直线l的斜率是1
(2)当m为何值时,直线l的倾斜角为90°
延伸探究1 本例条件不变,试求直线l的倾斜角为锐角时实数m的取值范围.
延伸探究2 若将本例中的“N(2m,1)”改为“N(3m,2m)”,其他条件不变,结果如何
直线斜率的计算方法
(1)判断两点的横坐标是否相等,若相等,则直线的斜率不存在.
(2)若两点的横坐标不相等,则可以用斜率公式k=(其中x1≠x2)进行计算.
金题典例 光线从点A(2,1)射到y轴上的点Q,经y轴反射后过点B(4,3),试求点Q的坐标
及入射光线的斜率.
光的反射问题中,反射角等于入射角,但反射光线的斜率并不等于入射光线的斜率.当镜面水平放置时,它们之间是互为相反数的关系.另外,在光的反射问题中也经常使用对称的方法求解.
跟踪训练2 一束光线从点A(-2,3)射入,经x轴上点P反射后,通过点B(5,7),求点P的坐标.
1.若直线l经过第二、第四象限,则直线l的倾斜角范围是( )
A.0°≤α<90° B.90°≤α<180° C.90°<α<180° D.0°<α<180°
2.过点A(-)与点B(-)的直线的倾斜角为( )
A.45° B.135° C.45°或135° D.60°
3.过点P(-2,m),Q(m,4)的直线的斜率为1,那么m的值为( )
A.1或4 B.4 C.1或3 D.1
4.光线从点A(-2,)射到x轴上的B点后,被x轴反射,这时反射光线恰好过点C(1,2),则光线BC所在直线的倾斜角为 .
5.直线l过点P(1,0),且与以A(2,1),B(0,)为端点的线段有公共点,求直线l的斜率和倾斜角的取值范围.
参考答案:
知识梳理
1.答案:C
2.答案:90°
3.【解析】 (1)× 倾斜角为90°时,斜率不存在.
(2)× 斜率应为-1.(3)× 斜率有可能不存在.(4)√
4. 答案:45° ∵k=tan α=1.∴α=45°.
5. 答案:D 由图可知,k1<0,k2>k3>0.故选D.
6. 答案:A
学习过程
例1 思路分析:画草图→标记α→找倾斜角与α的关系→求倾斜角
解:由题意画出如下草图.由图可知:
当α为钝角时,倾斜角为α-90°,
当α为锐角时,倾斜角为α+90°,
当α为直角时,倾斜角为0°.
综上,直线l转动前的倾斜角为
跟踪训练1. 解析:根据题意,画出图形,如图所示:因为0°≤α<180°,显然A,B,C未分类讨论,均不全面,不合题意.通过画图(如图所示)可知:当0°≤α<135°时,l1的倾斜角为α+45°;当135°≤α<180°时,l1的倾斜角为45°+α-180°=α-135°.故选D.
答案:D
例2 解:(1)kMN==1,解得m=.
(2)l的倾斜角为90°,即l平行于y轴,所以m+1=2m,得m=1.
延伸探究1 解:由题意知>0,解得1延伸探究2 解:(1)由题意知=1,解得m=2.
(2)由题意知m+1=3m,解得m=.
金题典例 解:(方法1)设Q(0,y),则由题意得kQA=-kQB.
∵kQA=,kQB=,∴=-.
解得y=,即点Q的坐标为0,,
∴k入=kQA==-.
(方法2)设Q(0,y),如图,点B(4,3)关于y轴的对称点为B'(-4,3),
kAB'==-,由题意得,A、Q、B'三点共线.
从而入射光线的斜率为kAQ=kAB'=-.
所以,有,解得y=,点Q的坐标为(0,).
跟踪训练2 解:(方法1)由光的反射原理,知kAP=-kBP,
设P(x,0),则=-,解得x=,即点P的坐标是(,0).
(方法2)由题意,知x轴是镜面,入射点A(-2,3)关于x轴的对称点为A1(-2,-3),则点A1应在反射光线所在的直线上,即A1,P,B三点共线,即=kPB,,解得x=,即点P的坐标是(,0).
达标检测
1.答案:C
2.解析:kAB==1,故直线的倾斜角为45°.答案:A
3.解析:由k==1,得m=1. 答案:D
4.解析:点A(-2,)关于x轴的对称点为A'(-2,-),由物理知识知kBC=kA'C=,所以所求倾斜角为60°.
答案:60°
5. 【解析】如图所示.
∵kAP==1,kBP==-,
∴k∈(-∞,-]∪[1,+∞),
∴45°≤α≤120°.
1.在平面直角坐标系中,结合具体图形,探索确定直线位置的几何要素.
2.理解直线的倾斜角和斜率的概念.
3.掌握倾斜角和斜率之间的关系.
4.掌握过两点的直线斜率的计算公式.
重点:理解直线倾斜角和斜率的概念及其关系
难点:过两点的直线斜率的计算公式.
一、自主导学
一、直线的倾斜角
定义 当直线l与x轴相交时,以x轴为基准,x轴正向与直线l向上的方向之间所成的角α叫做直线l的倾斜角
规定 当直线l与x轴平行或重合时,规定直线l的倾斜角为0°
记法 α
图示
范围 0°≤α<180°
作用 (1)表示平面直角坐标系内一条直线的倾斜程度; (2)确定平面直角坐标系中一条直线位置的几何要素是:直线上的一个定点以及它的倾斜角,二者缺一不可
点睛:倾斜角还可以这样定义:在平面直角坐标系中,对于一条与x轴相交的直线,把x轴所在的直线绕着交点按逆时针方向旋转到和直线重合时所转过的最小正角称为这条直线的倾斜角.并规定:与x轴平行或重合的直线的倾斜角为0°.
二、直线的斜率
1.定义与表示
定义(α为直线的倾 斜角) α≠90° 一条直线的倾斜角α的正切值叫做这条直线的斜率
α=90° 直线斜率不存在
记法 常用小写字母k表示,即k=tan α
范围 R
作用 用实数反映了平面直角坐标系内的直线的倾斜程度
2.填表:斜率与倾斜角的对应关系
90°;0; (0,+∞); (-∞,0)
3.我们知道,两点也可以唯一确定一条直线。
如果知道直线上的两点,怎么样来求直线的斜率(倾斜角)呢?
(
y
x
P
1
xy
Oxy
P
2
·
·
Q
)
当为锐角时,,,,在中,
若为钝角呢?你还能用其它方法推导这个公式吗?
三、直线的斜率公式
如果直线经过两点P1(x1,y1),P2(x2,y2),(x1≠x2),则直线的斜率公式为k=.
点睛:1.运用公式的前提是x1≠x2,即直线不与x轴垂直.
2.斜率公式与P1,P2在直线上的位置无关,在直线上任取两点,得到的斜率是相同的.
3.需注意公式中横、纵坐标之差的顺序,也可以写成k=.即下标的顺序一致.
二、小试牛刀
1.下列图中表示直线倾斜角为( )
2.直线x=1的倾斜角α= .
3.思考辨析
(1)任一直线都有倾斜角,都存在斜率.( )
(2)倾斜角为135°的直线的斜率为1.( )
(3)若一条直线的倾斜角为α,则它的斜率为k=tan α.( )
(4)直线斜率的取值范围是(-∞,+∞).( )
4.一条直线的斜率等于1,则此直线的倾斜角等于________.
5.如图,直线l1,l2,l3的斜率分别为k1,k2,k3,则( )
A.k1<k2<k3 B.k3<k1<k2 C.k3<k2<k1 D.k1<k3<k2
6.已知点P1(3,5),P2(-1,-3),则直线P1P2的斜率k等于( )
A.2 B.1 C.D.不存在
一、情境导学
交通工程上一般用“坡度”来描述一段道路对于水平方向的倾斜程度,如图,一辆汽车沿某条道路从A点前进到B点,在水平方向前进的距离为AD,竖直方向上升的高度为DB(如果是下降,则DB的值为负实数),则坡度k=.k>0表示上坡,k<0表示下坡,为了实际应用与安全,在道路铺设时常要规划坡度的大小.那么“坡度”是如何来刻画道路的倾斜程度的呢
二、典例解析
例1 已知直线l过原点,l绕原点按顺时针方向转动角α(0°<α<180°)后,恰好与y轴重合,求直线l转动前的倾斜角是多少
直线的倾斜角的求法
求直线的倾斜角主要根据定义,其关键是根据题意画出图形,找准倾斜角,有时要根据情况分类讨论.
跟踪训练1. 设直线l过坐标原点,它的倾斜角为α,如果将l绕坐标原点按逆时针方向旋转45°,得到直线l1,那么l1的倾斜角为( )
A.α+45° B.α-135°
C.135°-α D.当0°≤α<135°时,倾斜角为α+45°;当135°≤α<180°时,倾斜角为α-135°
例2 已知直线l过点M(m+1,m-1),N(2m,1).
(1)当m为何值时,直线l的斜率是1
(2)当m为何值时,直线l的倾斜角为90°
延伸探究1 本例条件不变,试求直线l的倾斜角为锐角时实数m的取值范围.
延伸探究2 若将本例中的“N(2m,1)”改为“N(3m,2m)”,其他条件不变,结果如何
直线斜率的计算方法
(1)判断两点的横坐标是否相等,若相等,则直线的斜率不存在.
(2)若两点的横坐标不相等,则可以用斜率公式k=(其中x1≠x2)进行计算.
金题典例 光线从点A(2,1)射到y轴上的点Q,经y轴反射后过点B(4,3),试求点Q的坐标
及入射光线的斜率.
光的反射问题中,反射角等于入射角,但反射光线的斜率并不等于入射光线的斜率.当镜面水平放置时,它们之间是互为相反数的关系.另外,在光的反射问题中也经常使用对称的方法求解.
跟踪训练2 一束光线从点A(-2,3)射入,经x轴上点P反射后,通过点B(5,7),求点P的坐标.
1.若直线l经过第二、第四象限,则直线l的倾斜角范围是( )
A.0°≤α<90° B.90°≤α<180° C.90°<α<180° D.0°<α<180°
2.过点A(-)与点B(-)的直线的倾斜角为( )
A.45° B.135° C.45°或135° D.60°
3.过点P(-2,m),Q(m,4)的直线的斜率为1,那么m的值为( )
A.1或4 B.4 C.1或3 D.1
4.光线从点A(-2,)射到x轴上的B点后,被x轴反射,这时反射光线恰好过点C(1,2),则光线BC所在直线的倾斜角为 .
5.直线l过点P(1,0),且与以A(2,1),B(0,)为端点的线段有公共点,求直线l的斜率和倾斜角的取值范围.
参考答案:
知识梳理
1.答案:C
2.答案:90°
3.【解析】 (1)× 倾斜角为90°时,斜率不存在.
(2)× 斜率应为-1.(3)× 斜率有可能不存在.(4)√
4. 答案:45° ∵k=tan α=1.∴α=45°.
5. 答案:D 由图可知,k1<0,k2>k3>0.故选D.
6. 答案:A
学习过程
例1 思路分析:画草图→标记α→找倾斜角与α的关系→求倾斜角
解:由题意画出如下草图.由图可知:
当α为钝角时,倾斜角为α-90°,
当α为锐角时,倾斜角为α+90°,
当α为直角时,倾斜角为0°.
综上,直线l转动前的倾斜角为
跟踪训练1. 解析:根据题意,画出图形,如图所示:因为0°≤α<180°,显然A,B,C未分类讨论,均不全面,不合题意.通过画图(如图所示)可知:当0°≤α<135°时,l1的倾斜角为α+45°;当135°≤α<180°时,l1的倾斜角为45°+α-180°=α-135°.故选D.
答案:D
例2 解:(1)kMN==1,解得m=.
(2)l的倾斜角为90°,即l平行于y轴,所以m+1=2m,得m=1.
延伸探究1 解:由题意知>0,解得1
(2)由题意知m+1=3m,解得m=.
金题典例 解:(方法1)设Q(0,y),则由题意得kQA=-kQB.
∵kQA=,kQB=,∴=-.
解得y=,即点Q的坐标为0,,
∴k入=kQA==-.
(方法2)设Q(0,y),如图,点B(4,3)关于y轴的对称点为B'(-4,3),
kAB'==-,由题意得,A、Q、B'三点共线.
从而入射光线的斜率为kAQ=kAB'=-.
所以,有,解得y=,点Q的坐标为(0,).
跟踪训练2 解:(方法1)由光的反射原理,知kAP=-kBP,
设P(x,0),则=-,解得x=,即点P的坐标是(,0).
(方法2)由题意,知x轴是镜面,入射点A(-2,3)关于x轴的对称点为A1(-2,-3),则点A1应在反射光线所在的直线上,即A1,P,B三点共线,即=kPB,,解得x=,即点P的坐标是(,0).
达标检测
1.答案:C
2.解析:kAB==1,故直线的倾斜角为45°.答案:A
3.解析:由k==1,得m=1. 答案:D
4.解析:点A(-2,)关于x轴的对称点为A'(-2,-),由物理知识知kBC=kA'C=,所以所求倾斜角为60°.
答案:60°
5. 【解析】如图所示.
∵kAP==1,kBP==-,
∴k∈(-∞,-]∪[1,+∞),
∴45°≤α≤120°.
