人教版数学八年级下册 18.1.2平行四边形的判定课件(共21张PPT)
文档属性
| 名称 | 人教版数学八年级下册 18.1.2平行四边形的判定课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 85.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-30 19:04:02 | ||
图片预览






文档简介
(共21张PPT)
八年级 下册
18.1.2 平行四边形的判定(1)
1、经历平行四边形判定定理的猜想与证明过程,体会类比思想及探究图形判定的一般思路;
2、掌握平行四边形的三个判定定理,能根据不同条件灵活选取适当的判定定理进行推理.
教学目标
重点:
平行四边形三个判定的探究与应用
难点:
平行四边形三个判定的应用
教学重难点
1、让学生理解平行四边形判定的猜想与证明过程.
2 掌握平行四边形的三个判定定理,能根据不同条件灵活选取适当的判定定理进行推理.
学习目标
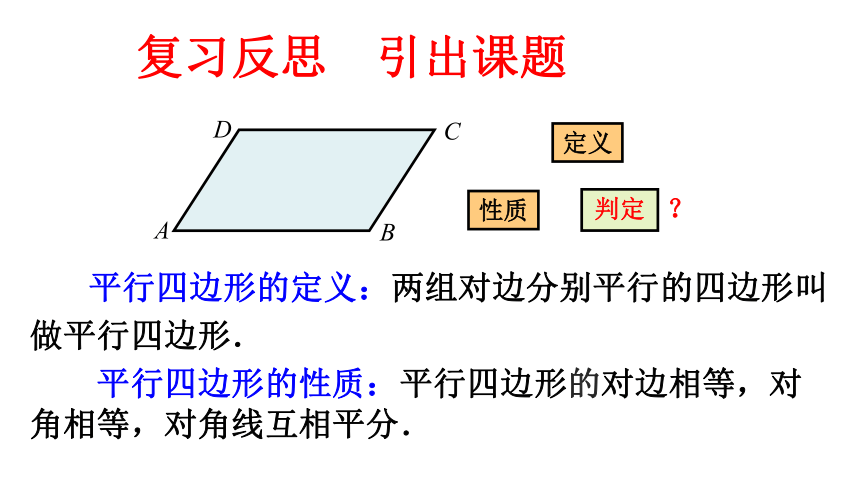
平行四边形的定义:两组对边分别平行的四边形叫
做平行四边形.
平行四边形的性质:平行四边形的对边相等,对角相等,对角线互相平分.
?
判定
性质
定义
复习反思 引出课题
D
A
B
C
自学指导
请同学们认真自学课本P.45—46思考 前面的内容,回答下列问题:
(1)如何寻找平行四边形的判定方法?
(2)平行四边形的判定方法有哪些?这些 结论是否正确?你能证明它们吗?
自学检测
两组对边分别相等的
四边形是平行四边形
平行四边形的性质
猜想 判断
平行四边形的两组对边相等
平行四边形的两组对角相等
平行四边形的对角线互相平分
两组对角分别相等的
四边形是平行四边形
对角线互相平分的四
边形是平行四边形
思考:这些猜想正确吗?
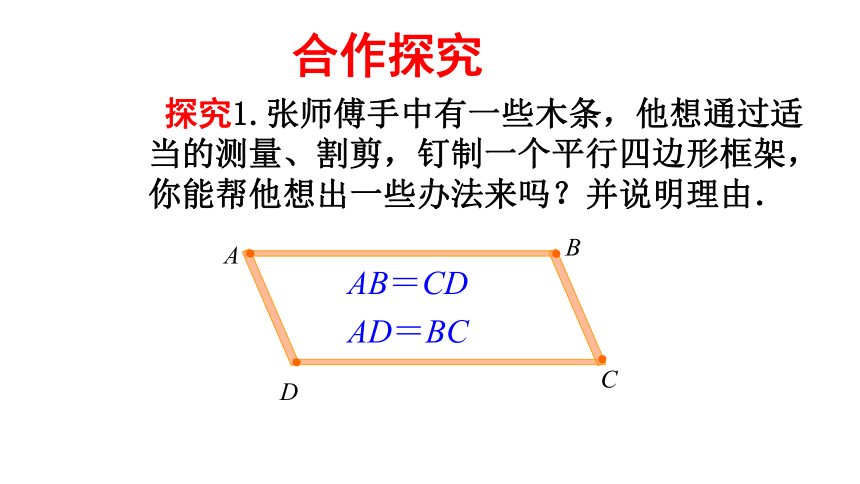
探究1.张师傅手中有一些木条,他想通过适当的测量、割剪,钉制一个平行四边形框架,你能帮他想出一些办法来吗?并说明理由.
●
●
●
●
A
C
B
D
AB=CD
AD=BC
合作探究
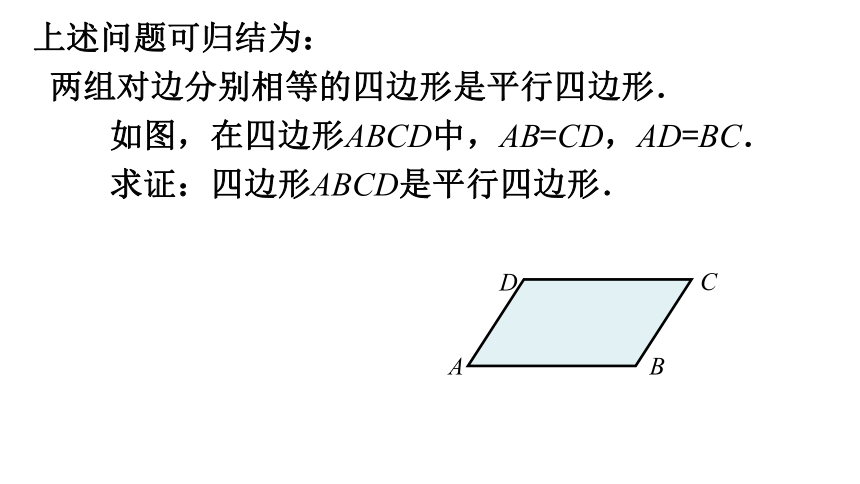
如图,在四边形ABCD中,AB=CD,AD=BC.
求证:四边形ABCD是平行四边形.
两组对边分别相等的四边形是平行四边形.
D
A
B
C
上述问题可归结为:
证明:连接BD.
∵ AB=CD,AD=BC,BD=DB
∴ △ABD≌△CDB.
∴ ∠1=∠2,∠3=∠4.
∴ AB∥DC,AD∥BC.
∴ 四边形ABCD是平行四边形.
D
A
B
C
1
2
3
4
探究2.将两根木条AC,BD的中点重叠,并用钉子固定,再用一根橡皮筋绕端点A,B,C,D围成一个四边行ABCD .想一想,△AOB ≌△COD吗?四边形ABCD的对边之间有什么关系?你得到什么结论?
A
C
B
O
D
如图,在四边形ABCD中,AC,BD相交于点O,且OA=OC,OB=OD.
求证:四边形ABCD是平行四边形.
对角线互相平分的四边形是平行四边形.
D
A
B
C
O
D
A
B
C
O
证明:∵ OA=OC,OB=OD,∠AOD=∠COB,
∴ △AOD≌△COB.
∴ ∠OAD=∠OCB.
∴ AD∥BC.
同理 AB∥DC.
∴ 四边形ABCD是平行四边形.
证明:∵ 多边形ABCD是四边形,
∴ ∠A+∠B+∠C+∠D=360°.
又∵ ∠A=∠C,∠B=∠D,
∴ ∠A+∠B=180°,
∠B+∠C=180°.
∴ AD∥BC,AB∥DC.
∴ 四边形ABCD是平行四边形.
如图,在四边形ABCD中,∠A=∠C,∠B=∠D.
求证:四边形ABCD是平行四边形.
探究3.两组对角分别相等的四边形是平行四边形.
D
A
B
C
现在,我们一共有哪些判定平行四边形的方法呢?
定义:两组对边分别平行的四边形叫做平行四边形.
判定定理:
(1)两组对边分别相等的四边形是平行四边形;
(2)两组对角分别相等的四边形是平行四边形;
(3)对角线互相平分的四边形是平行四边形.
阶段小结
1 如图,AB=DC=EF,AD=BC,DE=CF.
求证:AB∥EF.
A
B
C
D
E
F
当堂检测
证明:∵ AB=DC,AD=BC,
∴四边形ABCD是平行四边形.
∴ AB∥DC.
又∵ DC=EF,DE=CF,
∴ 四边形DCFE也是平行四边形.
∴ DC∥EF.
∴ AB∥EF.
1 如图,AB=DC=EF,AD=BC,DE=CF.求证:
AB∥EF.
A
B
C
D
E
F
2 如图, ABCD中,E,F分别是对角线AC 上的两点,并且 AE=CF.求证:四边形BFDE是平行四边形.
A
B
C
D
E
F
O
A
B
C
D
E
F
3 在上题中,若点E,F 分别在AC 两侧的延长线上,如图,其他条件不变,结论还成立吗?请证明你的结论.
知识的角度:
平行四边形的判定定理:
(1)两组对边分别相等的四边形是平行四边形;
(2)两组对角分别相等的四边形是平行四边形;
(3)对角线互相平分的四边形是平行四边形.
课堂小结
课堂小结
过程与方法的角度:
研究图形的一般思路.
解题策略的角度:
证明平行四边形有多种方法,应根据条件灵活应用.
性质
定义
判定
逆向猜想
八年级 下册
18.1.2 平行四边形的判定(1)
1、经历平行四边形判定定理的猜想与证明过程,体会类比思想及探究图形判定的一般思路;
2、掌握平行四边形的三个判定定理,能根据不同条件灵活选取适当的判定定理进行推理.
教学目标
重点:
平行四边形三个判定的探究与应用
难点:
平行四边形三个判定的应用
教学重难点
1、让学生理解平行四边形判定的猜想与证明过程.
2 掌握平行四边形的三个判定定理,能根据不同条件灵活选取适当的判定定理进行推理.
学习目标
平行四边形的定义:两组对边分别平行的四边形叫
做平行四边形.
平行四边形的性质:平行四边形的对边相等,对角相等,对角线互相平分.
?
判定
性质
定义
复习反思 引出课题
D
A
B
C
自学指导
请同学们认真自学课本P.45—46思考 前面的内容,回答下列问题:
(1)如何寻找平行四边形的判定方法?
(2)平行四边形的判定方法有哪些?这些 结论是否正确?你能证明它们吗?
自学检测
两组对边分别相等的
四边形是平行四边形
平行四边形的性质
猜想 判断
平行四边形的两组对边相等
平行四边形的两组对角相等
平行四边形的对角线互相平分
两组对角分别相等的
四边形是平行四边形
对角线互相平分的四
边形是平行四边形
思考:这些猜想正确吗?
探究1.张师傅手中有一些木条,他想通过适当的测量、割剪,钉制一个平行四边形框架,你能帮他想出一些办法来吗?并说明理由.
●
●
●
●
A
C
B
D
AB=CD
AD=BC
合作探究
如图,在四边形ABCD中,AB=CD,AD=BC.
求证:四边形ABCD是平行四边形.
两组对边分别相等的四边形是平行四边形.
D
A
B
C
上述问题可归结为:
证明:连接BD.
∵ AB=CD,AD=BC,BD=DB
∴ △ABD≌△CDB.
∴ ∠1=∠2,∠3=∠4.
∴ AB∥DC,AD∥BC.
∴ 四边形ABCD是平行四边形.
D
A
B
C
1
2
3
4
探究2.将两根木条AC,BD的中点重叠,并用钉子固定,再用一根橡皮筋绕端点A,B,C,D围成一个四边行ABCD .想一想,△AOB ≌△COD吗?四边形ABCD的对边之间有什么关系?你得到什么结论?
A
C
B
O
D
如图,在四边形ABCD中,AC,BD相交于点O,且OA=OC,OB=OD.
求证:四边形ABCD是平行四边形.
对角线互相平分的四边形是平行四边形.
D
A
B
C
O
D
A
B
C
O
证明:∵ OA=OC,OB=OD,∠AOD=∠COB,
∴ △AOD≌△COB.
∴ ∠OAD=∠OCB.
∴ AD∥BC.
同理 AB∥DC.
∴ 四边形ABCD是平行四边形.
证明:∵ 多边形ABCD是四边形,
∴ ∠A+∠B+∠C+∠D=360°.
又∵ ∠A=∠C,∠B=∠D,
∴ ∠A+∠B=180°,
∠B+∠C=180°.
∴ AD∥BC,AB∥DC.
∴ 四边形ABCD是平行四边形.
如图,在四边形ABCD中,∠A=∠C,∠B=∠D.
求证:四边形ABCD是平行四边形.
探究3.两组对角分别相等的四边形是平行四边形.
D
A
B
C
现在,我们一共有哪些判定平行四边形的方法呢?
定义:两组对边分别平行的四边形叫做平行四边形.
判定定理:
(1)两组对边分别相等的四边形是平行四边形;
(2)两组对角分别相等的四边形是平行四边形;
(3)对角线互相平分的四边形是平行四边形.
阶段小结
1 如图,AB=DC=EF,AD=BC,DE=CF.
求证:AB∥EF.
A
B
C
D
E
F
当堂检测
证明:∵ AB=DC,AD=BC,
∴四边形ABCD是平行四边形.
∴ AB∥DC.
又∵ DC=EF,DE=CF,
∴ 四边形DCFE也是平行四边形.
∴ DC∥EF.
∴ AB∥EF.
1 如图,AB=DC=EF,AD=BC,DE=CF.求证:
AB∥EF.
A
B
C
D
E
F
2 如图, ABCD中,E,F分别是对角线AC 上的两点,并且 AE=CF.求证:四边形BFDE是平行四边形.
A
B
C
D
E
F
O
A
B
C
D
E
F
3 在上题中,若点E,F 分别在AC 两侧的延长线上,如图,其他条件不变,结论还成立吗?请证明你的结论.
知识的角度:
平行四边形的判定定理:
(1)两组对边分别相等的四边形是平行四边形;
(2)两组对角分别相等的四边形是平行四边形;
(3)对角线互相平分的四边形是平行四边形.
课堂小结
课堂小结
过程与方法的角度:
研究图形的一般思路.
解题策略的角度:
证明平行四边形有多种方法,应根据条件灵活应用.
性质
定义
判定
逆向猜想
