沪科版数学七年级下册 10.1相交线 课件(共15张PPT)
文档属性
| 名称 | 沪科版数学七年级下册 10.1相交线 课件(共15张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 414.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-30 18:58:03 | ||
图片预览



文档简介
(共15张PPT)
沪科版教材七年级下册第十章第一节
10.1相交线
同学们五一刚放过假,有没有和老朋友一起聚一聚?和老朋友在一起度过的时间是不是非常的愉快!
我们人生的各个阶段都会有不同的朋友。如果把每个人的人生比作一条直线,我们从刚开始从互不相识,到后来的相识、相知,再到后来可能因为各种各样的原因,彼此远离,如果用我们数学上的几何图形来表示的话,可以把它们表示成什么?
一、创设情景激兴趣
对,就是相交线!
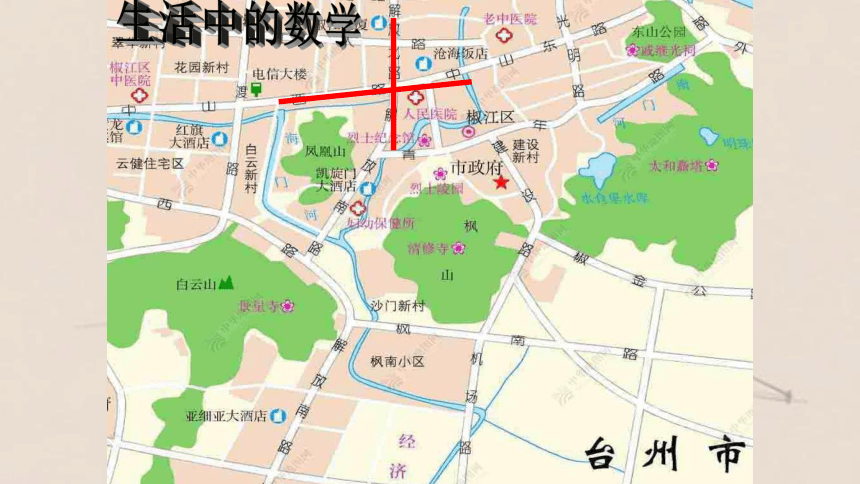
生活中的数学
生活中的数学
探究一 观察、讨论
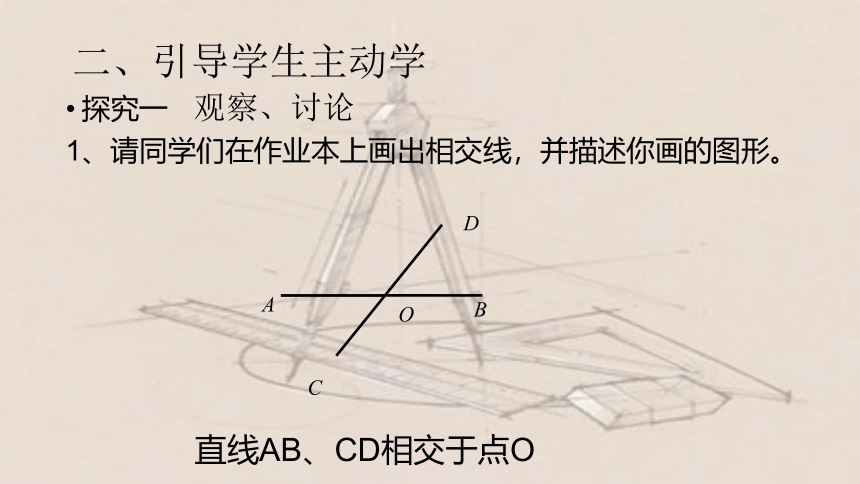
1、请同学们在作业本上画出相交线,并描述你画的图形。
二、引导学生主动学
直线AB、CD相交于点O
A
B
C
D
O
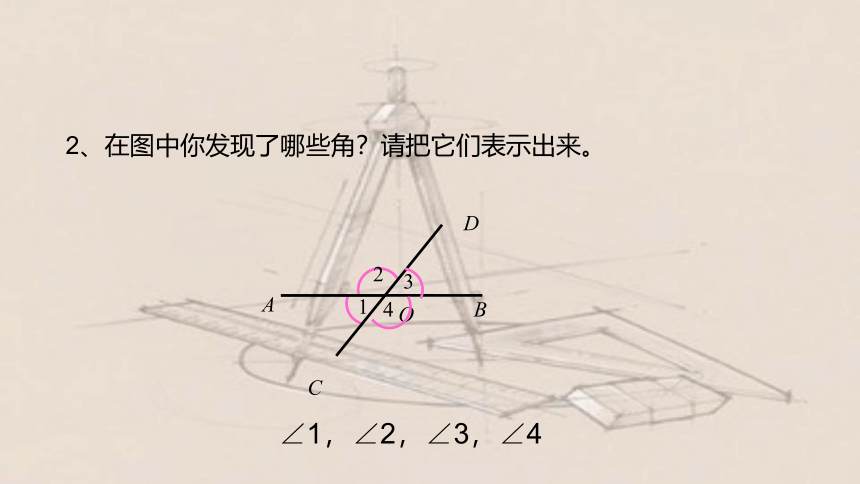
2、在图中你发现了哪些角?请把它们表示出来。
A
B
C
D
O
1
2
3
4
∠1,∠2,∠3,∠4
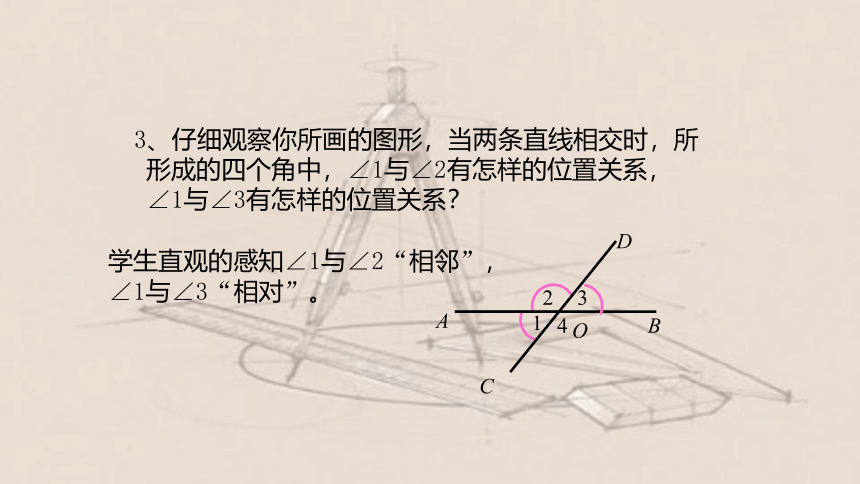
3、仔细观察你所画的图形,当两条直线相交时,所形成的四个角中,∠1与∠2有怎样的位置关系,∠1与∠3有怎样的位置关系?
A
B
C
D
O
1
2
3
4
学生直观的感知∠1与∠2“相邻”,
∠1与∠3“相对”。
1
A
C
3
O
B
D
已知一个角,画出与它“相对”的另一个角。
学生发现∠AOC与∠BOD有公共顶点O,而且
∠BOD的两边分别是∠AOC两边的反向延长线。
至此,可以得出:
对顶角的两个特征:
(1)有公共顶点,
(2)它们的两边分别互为反向延长线
你发现了什么?
定义:如果两个角有一个公共顶点,并且它们的两边分别互为反向延长线,那么这样的两个角叫做对顶角。
总结:对顶角是成对出现的,只有当两直线相交时才能产生对顶角。
判断下列各图中∠1与∠2是否互为对顶角?并说明理由.
1
1
1
1
1
1
1
2
(1)
(2)
(3)
(4)
(5)
(6)
2
2
2
2
2
三、巩固概念
右边是两根硬纸片,其中一根经旋转后,两根硬纸片所成的角度发生了变化.
猜一猜,在硬纸片转动的过程中。∠1与∠3这两个角的大小保持怎样的关系?先思考,再小组交流讨论。
A
B
C
D
O
1
3
四、操作观察,深入探究
1
2
(1)通过测量;(2)理论证明
由∠1+∠2=180°,∠2+∠3=180°,得
∠1=∠3(同角的补角相等),
由此可得到性质,对顶角相等。
∠1与∠3始终保持相等。
如图,直线a,b相交于点O,∠1 = ,
求∠2 ,∠3 ,∠4 的度数.
1
2
3
4
a
b
O
变式2 若∠2是∠1的 3.5倍,
求各个角的度数.
变式1 若∠1+∠3= 80 ,
求各个角的度数.
变式3 若 ∠1: ∠2 = 2: 7 ,
求各个角的度数.
五、尝试应用,变式训练
六、反思总结
本节课你有哪些收获?还有哪些疑问?还想进一步探究的问题是什么?
(引导学生在三维目标上谈收获。)
基础题:课本第121页 习题10.1第1.2两题
拓展题:研究拓展,当有n条直线相交于同一点时,有多少对对顶角?(用n的代数表示)
七、分层作业
说板书设计
1、对顶角的概念
2、对顶角的性质
(图形语言、文字语言、符号语言)
10.1相交线
沪科版教材七年级下册第十章第一节
10.1相交线
同学们五一刚放过假,有没有和老朋友一起聚一聚?和老朋友在一起度过的时间是不是非常的愉快!
我们人生的各个阶段都会有不同的朋友。如果把每个人的人生比作一条直线,我们从刚开始从互不相识,到后来的相识、相知,再到后来可能因为各种各样的原因,彼此远离,如果用我们数学上的几何图形来表示的话,可以把它们表示成什么?
一、创设情景激兴趣
对,就是相交线!
生活中的数学
生活中的数学
探究一 观察、讨论
1、请同学们在作业本上画出相交线,并描述你画的图形。
二、引导学生主动学
直线AB、CD相交于点O
A
B
C
D
O
2、在图中你发现了哪些角?请把它们表示出来。
A
B
C
D
O
1
2
3
4
∠1,∠2,∠3,∠4
3、仔细观察你所画的图形,当两条直线相交时,所形成的四个角中,∠1与∠2有怎样的位置关系,∠1与∠3有怎样的位置关系?
A
B
C
D
O
1
2
3
4
学生直观的感知∠1与∠2“相邻”,
∠1与∠3“相对”。
1
A
C
3
O
B
D
已知一个角,画出与它“相对”的另一个角。
学生发现∠AOC与∠BOD有公共顶点O,而且
∠BOD的两边分别是∠AOC两边的反向延长线。
至此,可以得出:
对顶角的两个特征:
(1)有公共顶点,
(2)它们的两边分别互为反向延长线
你发现了什么?
定义:如果两个角有一个公共顶点,并且它们的两边分别互为反向延长线,那么这样的两个角叫做对顶角。
总结:对顶角是成对出现的,只有当两直线相交时才能产生对顶角。
判断下列各图中∠1与∠2是否互为对顶角?并说明理由.
1
1
1
1
1
1
1
2
(1)
(2)
(3)
(4)
(5)
(6)
2
2
2
2
2
三、巩固概念
右边是两根硬纸片,其中一根经旋转后,两根硬纸片所成的角度发生了变化.
猜一猜,在硬纸片转动的过程中。∠1与∠3这两个角的大小保持怎样的关系?先思考,再小组交流讨论。
A
B
C
D
O
1
3
四、操作观察,深入探究
1
2
(1)通过测量;(2)理论证明
由∠1+∠2=180°,∠2+∠3=180°,得
∠1=∠3(同角的补角相等),
由此可得到性质,对顶角相等。
∠1与∠3始终保持相等。
如图,直线a,b相交于点O,∠1 = ,
求∠2 ,∠3 ,∠4 的度数.
1
2
3
4
a
b
O
变式2 若∠2是∠1的 3.5倍,
求各个角的度数.
变式1 若∠1+∠3= 80 ,
求各个角的度数.
变式3 若 ∠1: ∠2 = 2: 7 ,
求各个角的度数.
五、尝试应用,变式训练
六、反思总结
本节课你有哪些收获?还有哪些疑问?还想进一步探究的问题是什么?
(引导学生在三维目标上谈收获。)
基础题:课本第121页 习题10.1第1.2两题
拓展题:研究拓展,当有n条直线相交于同一点时,有多少对对顶角?(用n的代数表示)
七、分层作业
说板书设计
1、对顶角的概念
2、对顶角的性质
(图形语言、文字语言、符号语言)
10.1相交线
