北师大版九年级数学下册3 垂径定理课件(共18张PPT)
文档属性
| 名称 | 北师大版九年级数学下册3 垂径定理课件(共18张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-30 22:51:42 | ||
图片预览





文档简介
(共18张PPT)
学习目标
情境引入
新知探究
课堂小结
随堂练习
经历探索并证明垂径定理及其逆定理的过程,发展推理能力.
如右图所示,“圆材埋壁”是我国古代数学著作《九章算术》中的问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何.”用几何语言可表述为:CD为☉O的直径,弦AB⊥CD于E,CE=1寸,AB=10寸,则直径CD的长为多少
【问题】
当弦AB⊥CD时,你能得出哪些相等的线段 相等的弧 相等的角
垂径定理
【做一做】如右图所示,AB是☉O的一条弦,作直径CD,使CD⊥AB,垂足为M.
问题1
此图是轴对称图形吗 如果是,其对称轴是什么
这个图是轴对称图形,对称轴是直径CD所在的直线.
问题2
你发现图中有哪些等量关系 说一说你的理由.
将这个图沿着直径CD折叠,发现AM与BM重合,∠CMA与∠CMB重合, ∠DMA与∠DMB重合, 重合, 重合,所以等量关系有AM=BM, ∠CMA=∠CMB=90°,∠DMA=∠DMB=90°, , .
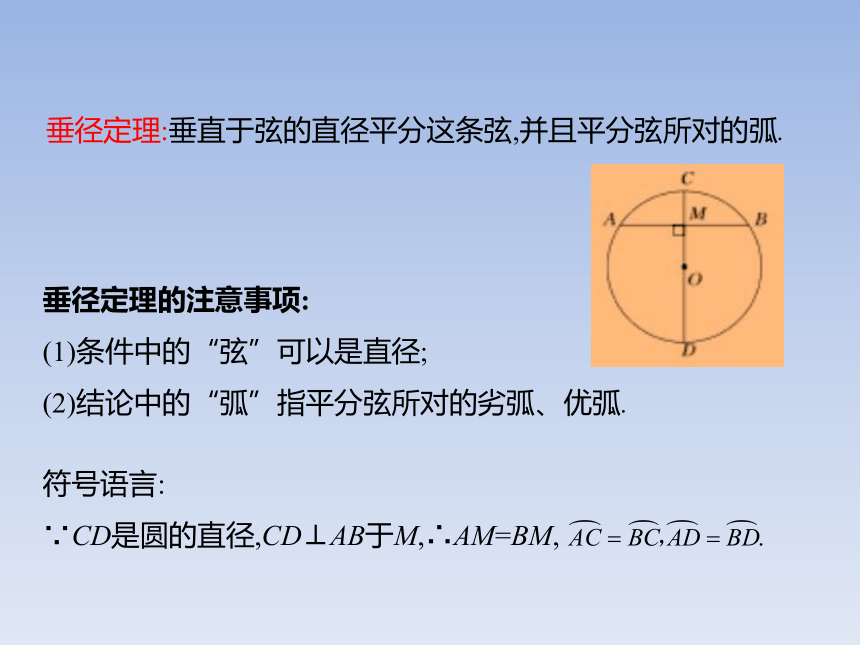
垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的弧.
垂径定理的注意事项:
(1)条件中的“弦”可以是直径;
(2)结论中的“弧”指平分弦所对的劣弧、优弧.
符号语言:
∵CD是圆的直径,CD⊥AB于M,∴AM=BM,
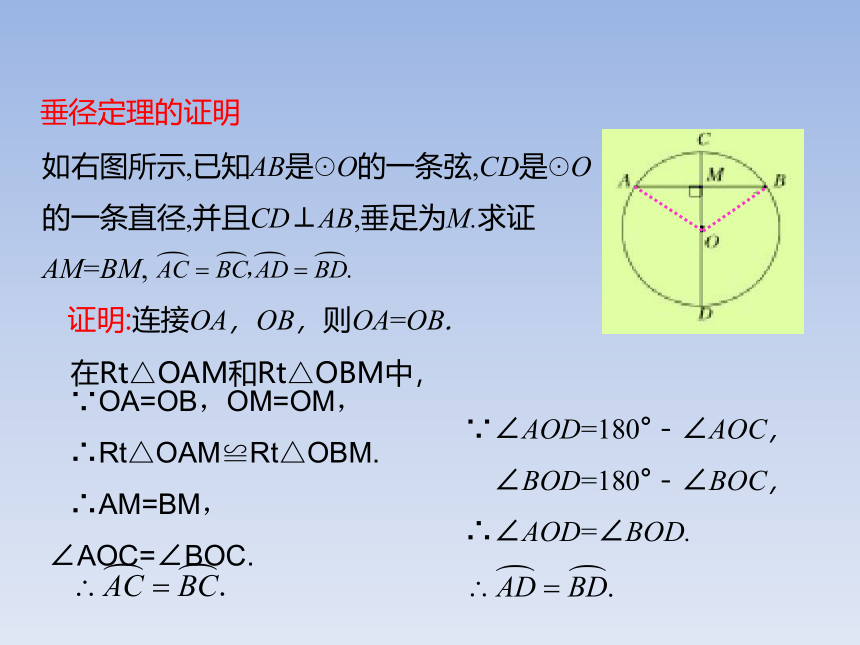
如右图所示,已知AB是☉O的一条弦,CD是☉O的一条直径,并且CD⊥AB,垂足为M.求证AM=BM,
垂径定理的证明
证明:连接OA,OB,则OA=OB.
在Rt△OAM和Rt△OBM中,
∵OA=OB,OM=OM,
∴Rt△OAM≌Rt△OBM.
∴AM=BM,∠AOC=∠BOC.
∵∠AOD=180°-∠AOC,
∠BOD=180°-∠BOC,
∴∠AOD=∠BOD.
判断下列图形,能否使用垂径定理?
【解析】定理中两个条件(直径,垂直于弦)缺一不可,故前三个图均不能,仅第四个图可以!
·
·
·
·
垂径定理的逆定理
如右图所示,AB是☉O的弦(不是直径),作一条平分AB的直径CD,交AB于M.
(1)此图是轴对称图形吗 如果是,其对称轴是什么
(2)你发现图中有哪些等量关系 说一说你的理由.
AM=BM,
OM=OM,
OA=OB,
△OAM≌△OBM.
∴∠AOC=∠BOC, ∠AMO=∠BMO=90°.
符号语言表示:
∵CD是圆的直径,CD平分AB (AB不是直径),
∴CD⊥AB,
思考下面的问题:
1.类比垂径定理的语言描述,你能总结得出结论吗
2.平分弦中的弦可以是直径吗
3.你得出的结论和垂径定理有什么区别
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的弧.
垂径定理的逆定理:
平分弦的直径垂直于弦,并且平分弦所对的弧.
知二推三:
①直径、
②垂直于弦、
③平分弦、
④平分优弧、
⑤平分劣弧
四个结论中,已知其中的两个结论就可以推导出其他的三个结论.
例 如右图所示,一条公路的转弯处是一段圆弧(即图中 ,点O是 所在圆的圆心),其中CD=600 m,E为 上一点,且OE⊥CD,垂足为F,EF=90 m.求这段弯路的半径.
〔解析〕连接OC,根据垂径定理可得CF=300 m,设圆弧的半径是R,OF=R-90,OC=R.
在Rt△OCF中,根据勾股定理可得OC的长,即可求得半径.
解:如图所示,连接OC,
设弯路的半径是R,则OF=(R-90)m.
∵OE⊥CD,
∴CF= CD= ×600=300(m).
在Rt△OCF中,根据勾股定理,
得OC2=CF2+OF2,
即R2=3002+(R-90)2,
解这个方程,得R=545.
所以这段弯路的半径是545 m.
1.如图所示,☉O的半径为5,弦AB的长为8,点M在线段AB(包括端点A,B)上移动,则OM的取值范围是 ( )
A.3≤OM≤5 B.3≤OM<5
C.4≤OM≤5 D.4≤OM<5
解析:当M与A或B重合时,OM达到最大值,即圆的半径5;当OM⊥AB时,OM取最小值,为 =3.故OM的取值范围是3≤OM≤5.故选A.
A
解析: ∵OC⊥弦AB于点C,
∴BC=AC= AB= ×4=2.
在Rt△OBC中,OC=1,BC=2,∴OB=
故填 .
2.如图所示,在☉O中,OC⊥弦AB于点C,AB=4,OC=1,则OB的长是 .
解析:连接OC,
∵CD⊥AB,CD=8,
∴PC= CD= ×8=4,
在Rt△OCP中,∵PC=4,OP=3,
∴OC=
故填5.
3.如图所示,AB是☉O的直径,弦CD⊥AB,垂足为P. 若CD=8,OP=3,则☉O的半径为 .
5
根据勾股定理,得OC= =5 cm,
∴CD=OD-OC=8 cm.
∴油面高CD为8 cm.
4.如图(1)所示, 水平放置的一个油管的截面半径为13 cm, 其中有油部分油面宽AB为24 cm, 求截面上有油部分油面高CD.
解析:根据垂径定理,易知AC,BC的长,连接OA,根据勾股定理即可求出OC的长,进而可求出CD的值.
解:如图(2)所示,连接OA.根据垂径定理,得AC=BC=12 cm.
在Rt△OAC中,OA=13 cm,AC=12 cm.
1. 垂径定理及其逆定理;
2.怎样利用垂径定理解决相应的数学问题.
学习目标
情境引入
新知探究
课堂小结
随堂练习
经历探索并证明垂径定理及其逆定理的过程,发展推理能力.
如右图所示,“圆材埋壁”是我国古代数学著作《九章算术》中的问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何.”用几何语言可表述为:CD为☉O的直径,弦AB⊥CD于E,CE=1寸,AB=10寸,则直径CD的长为多少
【问题】
当弦AB⊥CD时,你能得出哪些相等的线段 相等的弧 相等的角
垂径定理
【做一做】如右图所示,AB是☉O的一条弦,作直径CD,使CD⊥AB,垂足为M.
问题1
此图是轴对称图形吗 如果是,其对称轴是什么
这个图是轴对称图形,对称轴是直径CD所在的直线.
问题2
你发现图中有哪些等量关系 说一说你的理由.
将这个图沿着直径CD折叠,发现AM与BM重合,∠CMA与∠CMB重合, ∠DMA与∠DMB重合, 重合, 重合,所以等量关系有AM=BM, ∠CMA=∠CMB=90°,∠DMA=∠DMB=90°, , .
垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的弧.
垂径定理的注意事项:
(1)条件中的“弦”可以是直径;
(2)结论中的“弧”指平分弦所对的劣弧、优弧.
符号语言:
∵CD是圆的直径,CD⊥AB于M,∴AM=BM,
如右图所示,已知AB是☉O的一条弦,CD是☉O的一条直径,并且CD⊥AB,垂足为M.求证AM=BM,
垂径定理的证明
证明:连接OA,OB,则OA=OB.
在Rt△OAM和Rt△OBM中,
∵OA=OB,OM=OM,
∴Rt△OAM≌Rt△OBM.
∴AM=BM,∠AOC=∠BOC.
∵∠AOD=180°-∠AOC,
∠BOD=180°-∠BOC,
∴∠AOD=∠BOD.
判断下列图形,能否使用垂径定理?
【解析】定理中两个条件(直径,垂直于弦)缺一不可,故前三个图均不能,仅第四个图可以!
·
·
·
·
垂径定理的逆定理
如右图所示,AB是☉O的弦(不是直径),作一条平分AB的直径CD,交AB于M.
(1)此图是轴对称图形吗 如果是,其对称轴是什么
(2)你发现图中有哪些等量关系 说一说你的理由.
AM=BM,
OM=OM,
OA=OB,
△OAM≌△OBM.
∴∠AOC=∠BOC, ∠AMO=∠BMO=90°.
符号语言表示:
∵CD是圆的直径,CD平分AB (AB不是直径),
∴CD⊥AB,
思考下面的问题:
1.类比垂径定理的语言描述,你能总结得出结论吗
2.平分弦中的弦可以是直径吗
3.你得出的结论和垂径定理有什么区别
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的弧.
垂径定理的逆定理:
平分弦的直径垂直于弦,并且平分弦所对的弧.
知二推三:
①直径、
②垂直于弦、
③平分弦、
④平分优弧、
⑤平分劣弧
四个结论中,已知其中的两个结论就可以推导出其他的三个结论.
例 如右图所示,一条公路的转弯处是一段圆弧(即图中 ,点O是 所在圆的圆心),其中CD=600 m,E为 上一点,且OE⊥CD,垂足为F,EF=90 m.求这段弯路的半径.
〔解析〕连接OC,根据垂径定理可得CF=300 m,设圆弧的半径是R,OF=R-90,OC=R.
在Rt△OCF中,根据勾股定理可得OC的长,即可求得半径.
解:如图所示,连接OC,
设弯路的半径是R,则OF=(R-90)m.
∵OE⊥CD,
∴CF= CD= ×600=300(m).
在Rt△OCF中,根据勾股定理,
得OC2=CF2+OF2,
即R2=3002+(R-90)2,
解这个方程,得R=545.
所以这段弯路的半径是545 m.
1.如图所示,☉O的半径为5,弦AB的长为8,点M在线段AB(包括端点A,B)上移动,则OM的取值范围是 ( )
A.3≤OM≤5 B.3≤OM<5
C.4≤OM≤5 D.4≤OM<5
解析:当M与A或B重合时,OM达到最大值,即圆的半径5;当OM⊥AB时,OM取最小值,为 =3.故OM的取值范围是3≤OM≤5.故选A.
A
解析: ∵OC⊥弦AB于点C,
∴BC=AC= AB= ×4=2.
在Rt△OBC中,OC=1,BC=2,∴OB=
故填 .
2.如图所示,在☉O中,OC⊥弦AB于点C,AB=4,OC=1,则OB的长是 .
解析:连接OC,
∵CD⊥AB,CD=8,
∴PC= CD= ×8=4,
在Rt△OCP中,∵PC=4,OP=3,
∴OC=
故填5.
3.如图所示,AB是☉O的直径,弦CD⊥AB,垂足为P. 若CD=8,OP=3,则☉O的半径为 .
5
根据勾股定理,得OC= =5 cm,
∴CD=OD-OC=8 cm.
∴油面高CD为8 cm.
4.如图(1)所示, 水平放置的一个油管的截面半径为13 cm, 其中有油部分油面宽AB为24 cm, 求截面上有油部分油面高CD.
解析:根据垂径定理,易知AC,BC的长,连接OA,根据勾股定理即可求出OC的长,进而可求出CD的值.
解:如图(2)所示,连接OA.根据垂径定理,得AC=BC=12 cm.
在Rt△OAC中,OA=13 cm,AC=12 cm.
1. 垂径定理及其逆定理;
2.怎样利用垂径定理解决相应的数学问题.
