沪科版七年级数学下册 10.1相交线(第1课时)(共31张PPT)
文档属性
| 名称 | 沪科版七年级数学下册 10.1相交线(第1课时)(共31张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-01 00:00:00 | ||
图片预览





文档简介
(共31张PPT)
10.1 相 交 线
沪科版七年级下册
第10章 相交线、平行线与平移
第一课时 对顶角
教学目标
1、如果两个角的和等于______,就说这两个角互为余角;
2、如果两个角的和等于______,就说这两个角互为补角.
3、角α的余角是 ,它的补角是 .
180°
90°
180°- α
90°- α
5、等角的余角 、等角的补角 ;
4、同角的余角 、同角的补角 ;
相等
相等
相等
相等
还记得这些知识吗?
知识回顾
A
B
C
D
O
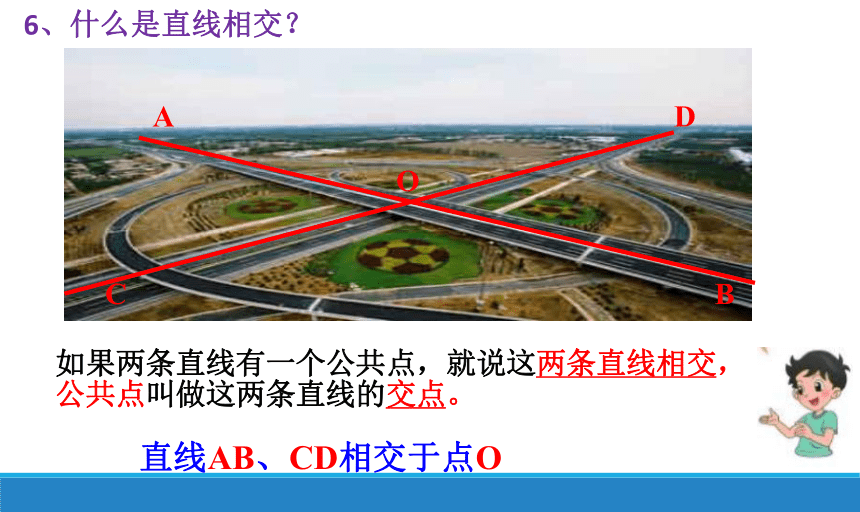
直线AB、CD相交于点O
如果两条直线有一个公共点,就说这两条直线相交,公共点叫做这两条直线的交点。
6、什么是直线相交?
情境导入
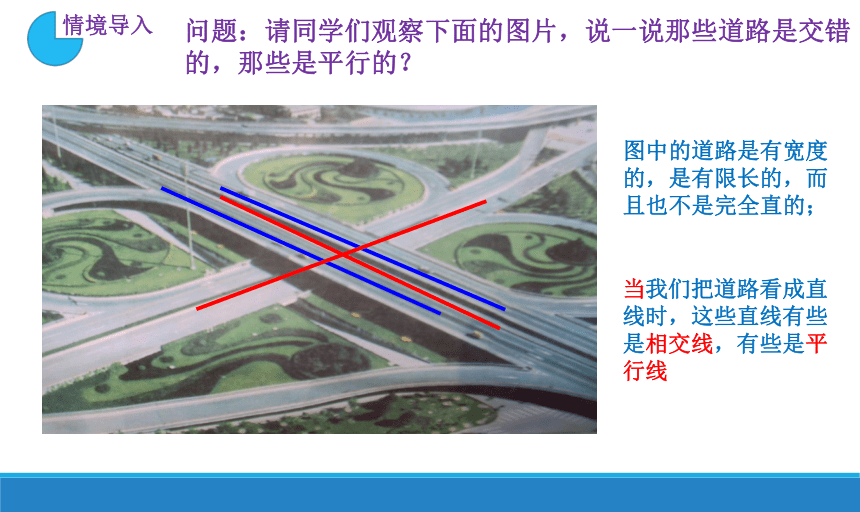
当我们把道路看成直线时,这些直线有些是相交线,有些是平行线
问题:请同学们观察下面的图片,说一说那些道路是交错的,那些是平行的?
图中的道路是有宽度的,是有限长的,而且也不是完全直的;
相交线和平行线是我们日常生活和生产中经常见到的,研究它们对今后的学习、工作和生活都很有用。
这节课 我们先来研究相交线。
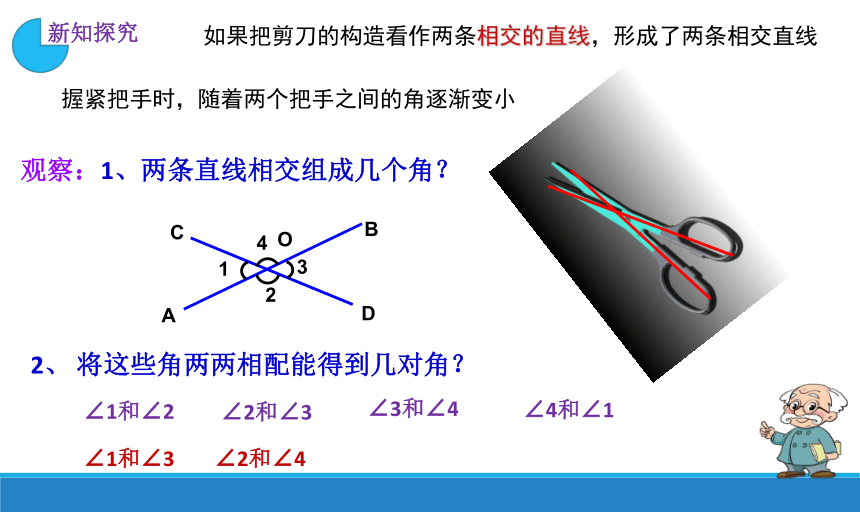
观察剪刀剪东西的过程,两个手柄构成的角和两片刀刃构成的角位置保持怎么的联系?
新知探究
握紧把手时,随着两个把手之间的角逐渐变小
如果把剪刀的构造看作两条相交的直线,形成了两条相交直线
观察:1、两条直线相交组成几个角?
2、 将这些角两两相配能得到几对角?
B
A
C
D
O
1
2
3
4
∠1和∠2
∠2和∠3
∠3和∠4
∠4和∠1
∠2和∠4
∠1和∠3
新知探究
2
1
3
2
3
4
1
4
C
D
B
A
1
3
4
2
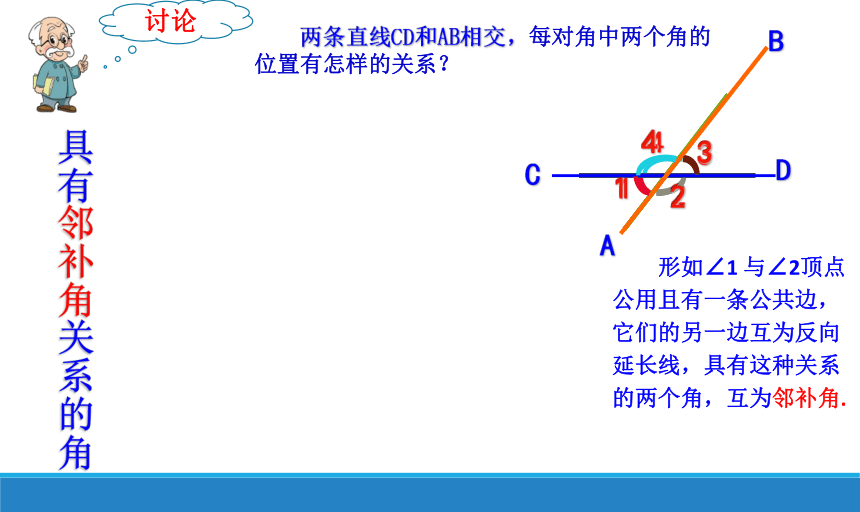
具有邻补角关系的角
形如∠1 与∠2顶点公用且有一条公共边,它们的另一边互为反向延长线,具有这种关系的两个角,互为邻补角.
两条直线CD和AB相交,每对角中两个角的位置有怎样的关系?
讨论
概念归纳
邻补角:
O
A
(
1
B
2
(
如果两个角有一条公共边,它们的另一边互为反向延长线,那么这两个角互为邻补角。
2、有一条公共边
3、另一边互为反向延长线
1、有公共顶点
邻补角特点:
C
C
D
B
A
1
3
4
2
4
2
3
1
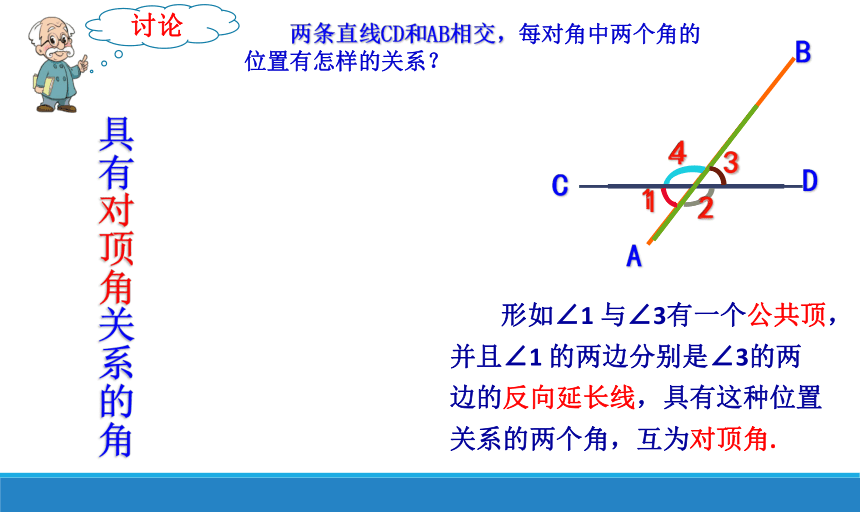
具有对顶角关系的角
形如∠1 与∠3有一个公共顶,并且∠1 的两边分别是∠3的两边的反向延长线,具有这种位置关系的两个角,互为对顶角.
两条直线CD和AB相交,每对角中两个角的位置有怎样的关系?
讨论
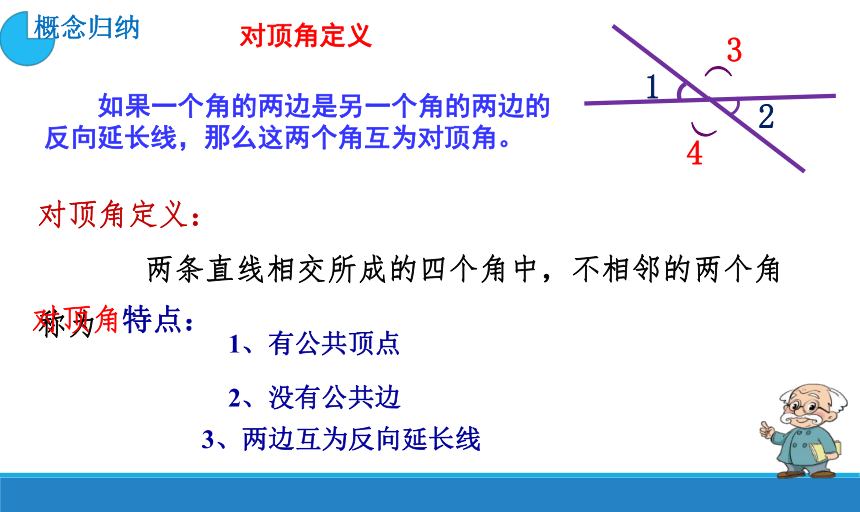
如果一个角的两边是另一个角的两边的反向延长线,那么这两个角互为对顶角。
对顶角定义:
两条直线相交所成的四个角中,不相邻的两个角称为
(
1
2
(
3
4
1、有公共顶点
2、没有公共边
3、两边互为反向延长线
对顶角特点:
概念归纳
对顶角定义
1、下列各图中∠1、∠2是对顶角吗?为什么?
1
2
)
(
1
2
(
)
1
2
(
)
概念辨析
不是
不是
不是
不符合对顶角的特征
2、下列各图中∠1、∠2是邻补角吗?为什么?
1
(
2
(
1
2
)
(
不是
是
不是
1
(
)
2
概念辨析
不符合邻补角的特征
1
2
3
4
1、如图,直线AB与CD相较于O点,∠1的邻补角有 个,是 ;
∠2和∠4
2
2、 ∵∠1+ ∠2= 和∠1+ ∠4= ;
∴∠2和∠4的大小关系 。
3、你能猜想出∠1和∠3的大小关系是 。
4、你有什么结论?
180°
180°
∠2=∠4
∠1=∠3
讨论
对顶角相等
新知探究
O
A
B
C
D
4
3
2
1
已知:直线AB与CD相交于O点(如图),试说明:∠1=∠3、 ∠2=∠4.
解:∵直线AB与CD相交于O点,
∴∠1+∠2=180°
∠2+∠3=180°,
∴∠1=∠3.
同理可得:∠2=∠4.
∵直线AB与CD相交于O点
∴∠1=∠3
对顶角性质定理:
对顶角相等
新知讲解
应用格式:
例1、如图,直线a、b相交于O
新知应用
1
2
3
4
(1)若∠1=40°32′,求出∠2、 ∠3、 ∠4的度数
解:
∵直线a、b相交于O
∴ ∠3= ∠1=40°32′(对顶角相等)
∵∠1+∠2=180°(邻补角定义)
∴ ∠2=180°- ∠1=180°-40°32′=139°28′
∴ ∠4= ∠2=139°28′(对顶角相等)
a
b
例1、如图,直线a、b相交于O
变式应用
1
2
3
4
(2)若∠1+∠3=50°,求出∠1、∠2、 ∠3、 ∠4的度数
解:
∵直线a、b相交于O
∴ ∠3= ∠1(对顶角相等)
∵∠1+∠3=50°(已知)
∴ ∠2=180°- ∠1=180°-25°=155°
∴ ∠4= ∠2=155°(对顶角相等)
a
b
∴ ∠3= ∠1=25°
∵∠1+∠2=180°(邻补角定义)
例1、如图,直线a、b相交于O
变式应用
1
2
3
4
(3)若∠1:∠2=2:7,求出∠1、∠2、 ∠3、 ∠4的度数
解:
∵直线a、b相交于O
∴ ∠3= ∠1=40°(对顶角相等)
∵∠1+∠2=180°(邻补角定义)
∴ ∠4= ∠2=140°(对顶角相等)
a
b
设∠1=2x°,则∠2=7x °
∴2x+7x=180
x=20
∴∠1=40°, ∠2=140°
角度计算题设未知数求解更方便
例2、如图,直线AB,CD相交于点O,若∠BOD=42°,OA平分∠COE,求∠AOE
∴∠AOC=∠BOD=42°(对顶角相等)
.∵OA平分∠COE,(已知)
∴∠COE=2∠AOC=84°(角平分线定义)
∵ ∠DOE+∠COE=180°(邻补角定义)
∴∠DOE=180°-∠COE
=180°-84°=96°.
C
O
E
42°
A
D
B
解:
∵直线AB,CD相交于点O
理论应用
你能举出生活中包含对顶角的例子吗
如图所示,有一个破损的扇形零件,怎样用量角器量出这个扇形零件的圆心角的度数.
A
O
B
C
D
扇形零件的圆心角∠BOC=∠AOD=60°
在下图中,花坛转角按图纸要求这个角(红色标注的角)为135°;施工结束后,要求你检测它是否合格?请你设计检测的方法.
1
2
理论应用
量出∠1的大小
根据∠2+∠1=180°计算出∠2的大小
根据对顶角相等,如果∠2=135°,则合格
1、如图,已知直线AE、BD相交于点C.
(1)图中哪些角是对顶角?
A
C
D
E
B
答:邻补角有四对:
∠ACB与∠ACD、∠ACB与∠BCE、
∠DCE与∠ACD、∠DCE与∠BCE.
答:对顶角有两对:
∠ACB与∠ECD、∠ACD与∠ECB.
(2)哪些角是邻补角?
课堂练习
2、下列图中有邻补角吗?有对顶角吗?如果有,请把它们指出来。
无对顶角,有两对邻补角:
∠AOC与∠BOC
∠AOD与∠BOD
无对顶角,有两对邻补角:
∠AOC与∠BOC
∠APD与∠BPD
无对顶角,有三 对邻补角:
∠AOC与∠BOC
∠AOD与∠BOD
∠AOE与∠BOE
无对顶角,有三 对邻补角:
∠AOE与∠BOE
∠AOC与∠BOC
∠AOD与∠BOD
A
B
C
D
O
A
B
C
D
O
E
A
B
C
D
O
E
(1)
(4)
(3)
A
B
C
D
O
P
(2)
课堂练习
3、如右图直线AB、CD交于点O,OE为射线,那么( )
A、∠AOC和∠BOE是对顶角;
B、∠COE和∠AOD是对顶角;
C、∠BOC和∠AOD是对顶角;
D、∠AOE和∠DOE是对顶角。
A
B
C
D
O
E
C
A
50°
?
4、如右图中直线AB、CD交于O,
OE是∠BOC的平分线且∠BOE=50度,那么∠AOC=( )度
(A)80; (B)100;
(C)130 (D)150。
c
b
a
1
2
3
4
∴∠4 =∠2=30°(对顶角相等 )
∴∠3=180 °-∠4-∠1
=180°-30°- 40°
=110°
提升练习
1、已知:三条直线 a、b、c 相交于O点,∠1=40°,∠2=30°,求∠3的度数
解:
直线 a、c 相交于O点
∵∠3+∠4+∠1=180 °(平角定义)
2、如图,直线AC,EF相交于点O,OD是∠AOB的平分线,OE在∠BOC内,∠BOE=∠EOC,∠DOE=72°,求∠AOF的度数.
∵OD平分∠AOB,
∴∠DOB=∠AOB= (180°-3x)
=90°-x
∵∠DOE=72°
提升练习
F
D
A
2x
x
O
E
B
C
2x
解:
设∠BOE=x,则∠EOC=2x
∵直线AC,EF相交于点O
∴∠AOB+ ∠BOC =180°(邻补角定义)
∴∠AOB=180°-3x
∴∠AOF=2x=72°
解得x=36°
∴∠AOF= ∠EOC=2x(对顶角相等)
∴90°- x+x=72°,
3、观察下列各图,寻找对顶角(不含平角)
⑸ 若有22条直线相交于一点,则可形成 对对顶角.
提升练习
图a
D
A
B
C
O
图b
D
A
B
C
图c
D
A
B
C
⑴ 如图a,图中共有 对对顶角;
O
O
⑵ 如图b,图中共有 对对顶角;
⑶ 如图c,图中共有 对对顶角;
(4)有n条直线相交于一点,则可形成 对对顶角;
2
6
12
n(n-1)
462
填空:1、如图,直线AB、CD交EF于点
G、H,∠2=∠3,∠1=70°。
求∠4的度数。
解:∵∠2=∠ ( )
∠1=70 °( )
∴∠2= (等量代换)
又∵ (已知)
∴∠3= ( )
∴∠4=180°—∠ = ( 的定义)
A
C
D
B
E
F
G
H
1
2
3
4
1
对顶角相等
已知
70°
∠2=∠3
70 °
等量代换
3
110 °
邻补角
拓展练习
1、如图1,三条直线AB、CD、
EF两两相交,在这个图形中,有
对顶角_____对,邻补角____ 对.
6
12
∠AOD
∠BOD
∠AOD
∠COE
∠3、
2、如图2,直线AB、CD
相交于O,OE是射线。则
∠3的对顶角是_____________,
∠1的对顶角是_____________,
∠1的邻补角是_____________,
∠2的邻补角是_____________。
练习:
图1
图2
1、有公共顶点
分类
∠1和∠2、∠2和∠3、∠3和∠4、∠4和∠1
∠1和∠3、
∠2和∠4、
1、有公共顶点
位置关系特征
邻补角
对顶角
邻补角互补
2、有一条公共边
3、另一边互为反向延长线
2、没有公共边
两直线相交
3、两边互为反向延长线
名称
大小关系
对顶角相等
B
A
C
D
O
1
2
3
4
1
3
1
2
课堂小结
完成下列表格填空
10.1 相 交 线
沪科版七年级下册
第10章 相交线、平行线与平移
第一课时 对顶角
教学目标
1、如果两个角的和等于______,就说这两个角互为余角;
2、如果两个角的和等于______,就说这两个角互为补角.
3、角α的余角是 ,它的补角是 .
180°
90°
180°- α
90°- α
5、等角的余角 、等角的补角 ;
4、同角的余角 、同角的补角 ;
相等
相等
相等
相等
还记得这些知识吗?
知识回顾
A
B
C
D
O
直线AB、CD相交于点O
如果两条直线有一个公共点,就说这两条直线相交,公共点叫做这两条直线的交点。
6、什么是直线相交?
情境导入
当我们把道路看成直线时,这些直线有些是相交线,有些是平行线
问题:请同学们观察下面的图片,说一说那些道路是交错的,那些是平行的?
图中的道路是有宽度的,是有限长的,而且也不是完全直的;
相交线和平行线是我们日常生活和生产中经常见到的,研究它们对今后的学习、工作和生活都很有用。
这节课 我们先来研究相交线。
观察剪刀剪东西的过程,两个手柄构成的角和两片刀刃构成的角位置保持怎么的联系?
新知探究
握紧把手时,随着两个把手之间的角逐渐变小
如果把剪刀的构造看作两条相交的直线,形成了两条相交直线
观察:1、两条直线相交组成几个角?
2、 将这些角两两相配能得到几对角?
B
A
C
D
O
1
2
3
4
∠1和∠2
∠2和∠3
∠3和∠4
∠4和∠1
∠2和∠4
∠1和∠3
新知探究
2
1
3
2
3
4
1
4
C
D
B
A
1
3
4
2
具有邻补角关系的角
形如∠1 与∠2顶点公用且有一条公共边,它们的另一边互为反向延长线,具有这种关系的两个角,互为邻补角.
两条直线CD和AB相交,每对角中两个角的位置有怎样的关系?
讨论
概念归纳
邻补角:
O
A
(
1
B
2
(
如果两个角有一条公共边,它们的另一边互为反向延长线,那么这两个角互为邻补角。
2、有一条公共边
3、另一边互为反向延长线
1、有公共顶点
邻补角特点:
C
C
D
B
A
1
3
4
2
4
2
3
1
具有对顶角关系的角
形如∠1 与∠3有一个公共顶,并且∠1 的两边分别是∠3的两边的反向延长线,具有这种位置关系的两个角,互为对顶角.
两条直线CD和AB相交,每对角中两个角的位置有怎样的关系?
讨论
如果一个角的两边是另一个角的两边的反向延长线,那么这两个角互为对顶角。
对顶角定义:
两条直线相交所成的四个角中,不相邻的两个角称为
(
1
2
(
3
4
1、有公共顶点
2、没有公共边
3、两边互为反向延长线
对顶角特点:
概念归纳
对顶角定义
1、下列各图中∠1、∠2是对顶角吗?为什么?
1
2
)
(
1
2
(
)
1
2
(
)
概念辨析
不是
不是
不是
不符合对顶角的特征
2、下列各图中∠1、∠2是邻补角吗?为什么?
1
(
2
(
1
2
)
(
不是
是
不是
1
(
)
2
概念辨析
不符合邻补角的特征
1
2
3
4
1、如图,直线AB与CD相较于O点,∠1的邻补角有 个,是 ;
∠2和∠4
2
2、 ∵∠1+ ∠2= 和∠1+ ∠4= ;
∴∠2和∠4的大小关系 。
3、你能猜想出∠1和∠3的大小关系是 。
4、你有什么结论?
180°
180°
∠2=∠4
∠1=∠3
讨论
对顶角相等
新知探究
O
A
B
C
D
4
3
2
1
已知:直线AB与CD相交于O点(如图),试说明:∠1=∠3、 ∠2=∠4.
解:∵直线AB与CD相交于O点,
∴∠1+∠2=180°
∠2+∠3=180°,
∴∠1=∠3.
同理可得:∠2=∠4.
∵直线AB与CD相交于O点
∴∠1=∠3
对顶角性质定理:
对顶角相等
新知讲解
应用格式:
例1、如图,直线a、b相交于O
新知应用
1
2
3
4
(1)若∠1=40°32′,求出∠2、 ∠3、 ∠4的度数
解:
∵直线a、b相交于O
∴ ∠3= ∠1=40°32′(对顶角相等)
∵∠1+∠2=180°(邻补角定义)
∴ ∠2=180°- ∠1=180°-40°32′=139°28′
∴ ∠4= ∠2=139°28′(对顶角相等)
a
b
例1、如图,直线a、b相交于O
变式应用
1
2
3
4
(2)若∠1+∠3=50°,求出∠1、∠2、 ∠3、 ∠4的度数
解:
∵直线a、b相交于O
∴ ∠3= ∠1(对顶角相等)
∵∠1+∠3=50°(已知)
∴ ∠2=180°- ∠1=180°-25°=155°
∴ ∠4= ∠2=155°(对顶角相等)
a
b
∴ ∠3= ∠1=25°
∵∠1+∠2=180°(邻补角定义)
例1、如图,直线a、b相交于O
变式应用
1
2
3
4
(3)若∠1:∠2=2:7,求出∠1、∠2、 ∠3、 ∠4的度数
解:
∵直线a、b相交于O
∴ ∠3= ∠1=40°(对顶角相等)
∵∠1+∠2=180°(邻补角定义)
∴ ∠4= ∠2=140°(对顶角相等)
a
b
设∠1=2x°,则∠2=7x °
∴2x+7x=180
x=20
∴∠1=40°, ∠2=140°
角度计算题设未知数求解更方便
例2、如图,直线AB,CD相交于点O,若∠BOD=42°,OA平分∠COE,求∠AOE
∴∠AOC=∠BOD=42°(对顶角相等)
.∵OA平分∠COE,(已知)
∴∠COE=2∠AOC=84°(角平分线定义)
∵ ∠DOE+∠COE=180°(邻补角定义)
∴∠DOE=180°-∠COE
=180°-84°=96°.
C
O
E
42°
A
D
B
解:
∵直线AB,CD相交于点O
理论应用
你能举出生活中包含对顶角的例子吗
如图所示,有一个破损的扇形零件,怎样用量角器量出这个扇形零件的圆心角的度数.
A
O
B
C
D
扇形零件的圆心角∠BOC=∠AOD=60°
在下图中,花坛转角按图纸要求这个角(红色标注的角)为135°;施工结束后,要求你检测它是否合格?请你设计检测的方法.
1
2
理论应用
量出∠1的大小
根据∠2+∠1=180°计算出∠2的大小
根据对顶角相等,如果∠2=135°,则合格
1、如图,已知直线AE、BD相交于点C.
(1)图中哪些角是对顶角?
A
C
D
E
B
答:邻补角有四对:
∠ACB与∠ACD、∠ACB与∠BCE、
∠DCE与∠ACD、∠DCE与∠BCE.
答:对顶角有两对:
∠ACB与∠ECD、∠ACD与∠ECB.
(2)哪些角是邻补角?
课堂练习
2、下列图中有邻补角吗?有对顶角吗?如果有,请把它们指出来。
无对顶角,有两对邻补角:
∠AOC与∠BOC
∠AOD与∠BOD
无对顶角,有两对邻补角:
∠AOC与∠BOC
∠APD与∠BPD
无对顶角,有三 对邻补角:
∠AOC与∠BOC
∠AOD与∠BOD
∠AOE与∠BOE
无对顶角,有三 对邻补角:
∠AOE与∠BOE
∠AOC与∠BOC
∠AOD与∠BOD
A
B
C
D
O
A
B
C
D
O
E
A
B
C
D
O
E
(1)
(4)
(3)
A
B
C
D
O
P
(2)
课堂练习
3、如右图直线AB、CD交于点O,OE为射线,那么( )
A、∠AOC和∠BOE是对顶角;
B、∠COE和∠AOD是对顶角;
C、∠BOC和∠AOD是对顶角;
D、∠AOE和∠DOE是对顶角。
A
B
C
D
O
E
C
A
50°
?
4、如右图中直线AB、CD交于O,
OE是∠BOC的平分线且∠BOE=50度,那么∠AOC=( )度
(A)80; (B)100;
(C)130 (D)150。
c
b
a
1
2
3
4
∴∠4 =∠2=30°(对顶角相等 )
∴∠3=180 °-∠4-∠1
=180°-30°- 40°
=110°
提升练习
1、已知:三条直线 a、b、c 相交于O点,∠1=40°,∠2=30°,求∠3的度数
解:
直线 a、c 相交于O点
∵∠3+∠4+∠1=180 °(平角定义)
2、如图,直线AC,EF相交于点O,OD是∠AOB的平分线,OE在∠BOC内,∠BOE=∠EOC,∠DOE=72°,求∠AOF的度数.
∵OD平分∠AOB,
∴∠DOB=∠AOB= (180°-3x)
=90°-x
∵∠DOE=72°
提升练习
F
D
A
2x
x
O
E
B
C
2x
解:
设∠BOE=x,则∠EOC=2x
∵直线AC,EF相交于点O
∴∠AOB+ ∠BOC =180°(邻补角定义)
∴∠AOB=180°-3x
∴∠AOF=2x=72°
解得x=36°
∴∠AOF= ∠EOC=2x(对顶角相等)
∴90°- x+x=72°,
3、观察下列各图,寻找对顶角(不含平角)
⑸ 若有22条直线相交于一点,则可形成 对对顶角.
提升练习
图a
D
A
B
C
O
图b
D
A
B
C
图c
D
A
B
C
⑴ 如图a,图中共有 对对顶角;
O
O
⑵ 如图b,图中共有 对对顶角;
⑶ 如图c,图中共有 对对顶角;
(4)有n条直线相交于一点,则可形成 对对顶角;
2
6
12
n(n-1)
462
填空:1、如图,直线AB、CD交EF于点
G、H,∠2=∠3,∠1=70°。
求∠4的度数。
解:∵∠2=∠ ( )
∠1=70 °( )
∴∠2= (等量代换)
又∵ (已知)
∴∠3= ( )
∴∠4=180°—∠ = ( 的定义)
A
C
D
B
E
F
G
H
1
2
3
4
1
对顶角相等
已知
70°
∠2=∠3
70 °
等量代换
3
110 °
邻补角
拓展练习
1、如图1,三条直线AB、CD、
EF两两相交,在这个图形中,有
对顶角_____对,邻补角____ 对.
6
12
∠AOD
∠BOD
∠AOD
∠COE
∠3、
2、如图2,直线AB、CD
相交于O,OE是射线。则
∠3的对顶角是_____________,
∠1的对顶角是_____________,
∠1的邻补角是_____________,
∠2的邻补角是_____________。
练习:
图1
图2
1、有公共顶点
分类
∠1和∠2、∠2和∠3、∠3和∠4、∠4和∠1
∠1和∠3、
∠2和∠4、
1、有公共顶点
位置关系特征
邻补角
对顶角
邻补角互补
2、有一条公共边
3、另一边互为反向延长线
2、没有公共边
两直线相交
3、两边互为反向延长线
名称
大小关系
对顶角相等
B
A
C
D
O
1
2
3
4
1
3
1
2
课堂小结
完成下列表格填空
