2.1.1倾斜角与斜率 课件(共19张PPT)
文档属性
| 名称 | 2.1.1倾斜角与斜率 课件(共19张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-29 12:39:02 | ||
图片预览


文档简介
(共19张PPT)
2.1 直线的倾斜角与斜率
第二章 直线和圆的方程
2.1.1 倾斜角与斜率
我们知道,点是构成直线的基本元素.在平面直角坐标系中,可以用坐标表示点,那么,如何用坐标表示直线呢?
复习回顾
为了用代数方法研究直线的有关问题,本节我们首先在平面直角坐标系中探索确定直线位置的几何要素,然后用代数方法把这些几何要素表示出来.
思考:确定一条直线的几何要素是什么?对于平面直角生标系中的一条直线,如何利用坐标系确定它的位置?
两点确定一条直线,一点和一个方向也可以确定一条直线,设A,B为直线上的两点,则 就是这条直线的方向向量,所以,两点确定一条直线可以归结为一点和一个方向确定一条直线.
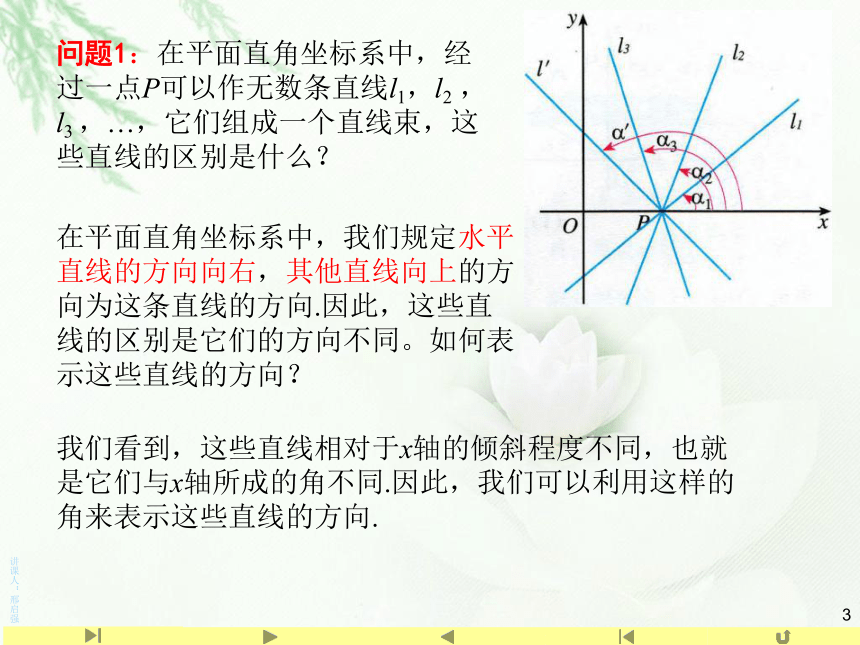
问题1:在平面直角坐标系中,经过一点P可以作无数条直线l1,l2 , l3 ,…,它们组成一个直线束,这些直线的区别是什么?
在平面直角坐标系中,我们规定水平直线的方向向右,其他直线向上的方向为这条直线的方向.因此,这些直线的区别是它们的方向不同。如何表示这些直线的方向?
我们看到,这些直线相对于x轴的倾斜程度不同,也就是它们与x轴所成的角不同.因此,我们可以利用这样的角来表示这些直线的方向.
直线的倾斜角
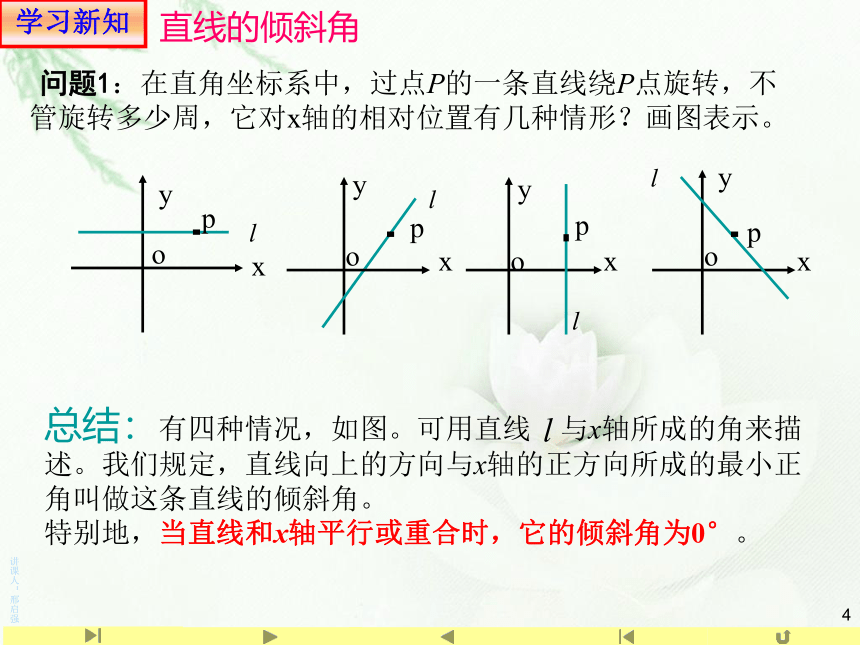
问题1:在直角坐标系中,过点P的一条直线绕P点旋转,不管旋转多少周,它对x轴的相对位置有几种情形?画图表示。
总结:有四种情况,如图。可用直线 与x轴所成的角来描述。我们规定,直线向上的方向与x轴的正方向所成的最小正角叫做这条直线的倾斜角。
特别地,当直线和x轴平行或重合时,它的倾斜角为0°。
p
o
y
x
y
p
o
x
p
o
y
x
p
o
y
x
学习新知
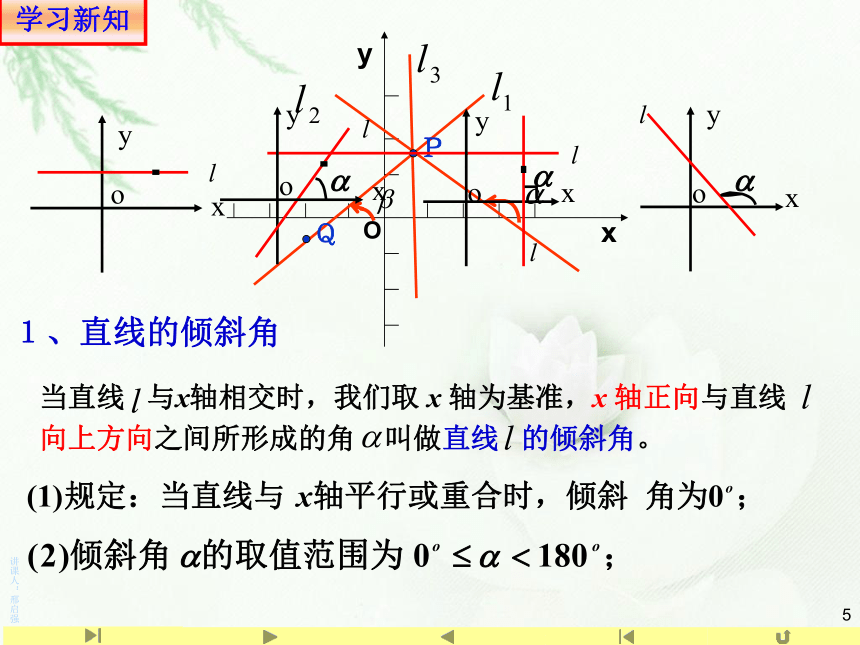
1、直线的倾斜角
当直线 与x轴相交时,我们取 x 轴为基准,x 轴正向与直线 向上方向之间所形成的角 叫做直线 的倾斜角。
O
x
y
Q
P
学习新知
o
y
x
o
y
x
y
o
x
o
y
x
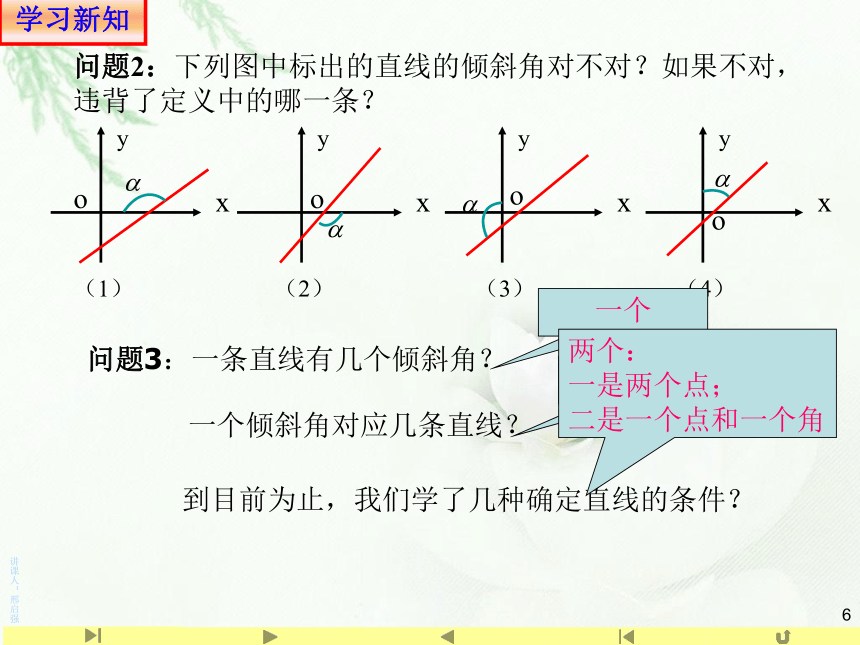
问题2:下列图中标出的直线的倾斜角对不对?如果不对,违背了定义中的哪一条?
x
y
o
x
y
o
x
y
o
x
y
o
(1)
(2)
(3)
(4)
问题3:一条直线有几个倾斜角?
一个倾斜角对应几条直线?
到目前为止,我们学了几种确定直线的条件?
一个
无数条
两个:
一是两个点;
二是一个点和一个角
学习新知
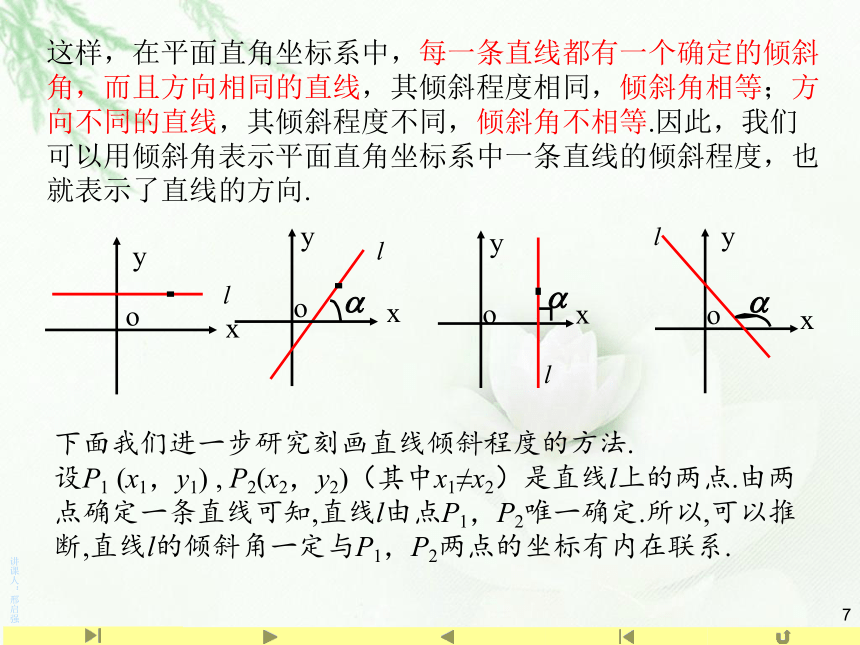
这样,在平面直角坐标系中,每一条直线都有一个确定的倾斜角,而且方向相同的直线,其倾斜程度相同,倾斜角相等;方向不同的直线,其倾斜程度不同,倾斜角不相等.因此,我们可以用倾斜角表示平面直角坐标系中一条直线的倾斜程度,也就表示了直线的方向.
下面我们进一步研究刻画直线倾斜程度的方法.
设P1 (x1,y1) , P2(x2,y2)(其中x1≠x2)是直线l上的两点.由两点确定一条直线可知,直线l由点P1,P2唯一确定.所以,可以推断,直线l的倾斜角一定与P1,P2两点的坐标有内在联系.
o
y
x
o
y
x
y
o
x
o
y
x
下面我们利用向量法探究上述问题
探究在平面直角坐标系中,设直线l的倾斜角为
(1)已知直线l经过O(0,0),P( ,1), 与O,P的坐标有什么关系?
(2)类似地,如果直线l经过P1(-1,1),P2( ,0) , 与P1,P2的坐标又有什么关系?
(3)一般地,如果直线l经过两点P1 (x1,y1) ,P2 (x2,y2) ,x1≠x2,那么 与P1,P2的坐标有怎样的关系?
学习新知
学习新知
思考 当直线P1P2与x轴平行或重合时,上述式子还成立吗?为什么?
倾斜角是90°的直线没有斜率,倾斜角不是90°的直线都有斜率.
由正切函数的单调性,倾斜角不同的直线,其斜率也不同.因此,我们可以用斜率表示倾斜角不等于90°的直线相对于x轴的倾斜程度,进而表示直线的方向.
公式的特点:
(1)与两点的顺序无关;
(2) 公式表明,直线对于x轴的倾斜度,可以通过直线上任意两点的坐标来表示,而不需要求出直线的倾斜角;
(3)当x1=x2时,公式不适用,此时直线与x轴垂直,α=900
斜率公式
思考
(1)已知直线上的两点A(a1,a2),B(b1,b2),运用上述公式计算直线AB的斜率时,与A,B两点的顺序有关吗?
(2)当直线平行于y轴,或与y轴重合时,上述公式还适用吗?为什么?
一条直线倾斜角的正切值叫做这条直线的斜率。斜率通常用k表示,即:
2、直线的斜率
思考:日常生活中,还有没有表示倾斜程度的量呢?
前进
升高
注意:
学习新知
1 、两直线的斜率相等,它们的倾斜角也相等
2 、直线斜率的范围是R
(1)当 时,k随 增大而增大,且k≥0
(2)当 时,k随 增大而增大,且k<0
1.下列哪些说法是正确的( )
A 、任一条直线都有倾斜角,也都有斜率
B、直线的倾斜角越大,斜率也越大
C 、平行于x轴的直线的倾斜角是0°或180°
D. 一定点和一倾斜角可以唯一确定一条直线
D
达标练习
l1
l2
l3
k2>k3>k1
我们知道,直线P1P2上的向量 以及与它平行的向量都是直线的方向向量.直线P1P2的方向向量 的坐标为
例1 如下图,已知A(3,2),B(-4,1),C(0,-1),求直线AB,BC,CA的斜率,并判断这些直线的倾斜角是锐角还是纯角.
O
x
y
A
C
B
锐角
钝角
锐角
(2).过点C的直线l与线段AB有公共点,求l的斜率k的取值范围
典型例题
例2、在平面直角坐标系中,画出经过原点且斜率分别为1,-1,2和-3的直线 。
O
x
y
A3
A1
A2
A4
典型例题
1:直线的倾斜角的概念
2:直线的斜率
3:斜率公式
课堂小结
4:y=tanx的图象
2.1 直线的倾斜角与斜率
第二章 直线和圆的方程
2.1.1 倾斜角与斜率
我们知道,点是构成直线的基本元素.在平面直角坐标系中,可以用坐标表示点,那么,如何用坐标表示直线呢?
复习回顾
为了用代数方法研究直线的有关问题,本节我们首先在平面直角坐标系中探索确定直线位置的几何要素,然后用代数方法把这些几何要素表示出来.
思考:确定一条直线的几何要素是什么?对于平面直角生标系中的一条直线,如何利用坐标系确定它的位置?
两点确定一条直线,一点和一个方向也可以确定一条直线,设A,B为直线上的两点,则 就是这条直线的方向向量,所以,两点确定一条直线可以归结为一点和一个方向确定一条直线.
问题1:在平面直角坐标系中,经过一点P可以作无数条直线l1,l2 , l3 ,…,它们组成一个直线束,这些直线的区别是什么?
在平面直角坐标系中,我们规定水平直线的方向向右,其他直线向上的方向为这条直线的方向.因此,这些直线的区别是它们的方向不同。如何表示这些直线的方向?
我们看到,这些直线相对于x轴的倾斜程度不同,也就是它们与x轴所成的角不同.因此,我们可以利用这样的角来表示这些直线的方向.
直线的倾斜角
问题1:在直角坐标系中,过点P的一条直线绕P点旋转,不管旋转多少周,它对x轴的相对位置有几种情形?画图表示。
总结:有四种情况,如图。可用直线 与x轴所成的角来描述。我们规定,直线向上的方向与x轴的正方向所成的最小正角叫做这条直线的倾斜角。
特别地,当直线和x轴平行或重合时,它的倾斜角为0°。
p
o
y
x
y
p
o
x
p
o
y
x
p
o
y
x
学习新知
1、直线的倾斜角
当直线 与x轴相交时,我们取 x 轴为基准,x 轴正向与直线 向上方向之间所形成的角 叫做直线 的倾斜角。
O
x
y
Q
P
学习新知
o
y
x
o
y
x
y
o
x
o
y
x
问题2:下列图中标出的直线的倾斜角对不对?如果不对,违背了定义中的哪一条?
x
y
o
x
y
o
x
y
o
x
y
o
(1)
(2)
(3)
(4)
问题3:一条直线有几个倾斜角?
一个倾斜角对应几条直线?
到目前为止,我们学了几种确定直线的条件?
一个
无数条
两个:
一是两个点;
二是一个点和一个角
学习新知
这样,在平面直角坐标系中,每一条直线都有一个确定的倾斜角,而且方向相同的直线,其倾斜程度相同,倾斜角相等;方向不同的直线,其倾斜程度不同,倾斜角不相等.因此,我们可以用倾斜角表示平面直角坐标系中一条直线的倾斜程度,也就表示了直线的方向.
下面我们进一步研究刻画直线倾斜程度的方法.
设P1 (x1,y1) , P2(x2,y2)(其中x1≠x2)是直线l上的两点.由两点确定一条直线可知,直线l由点P1,P2唯一确定.所以,可以推断,直线l的倾斜角一定与P1,P2两点的坐标有内在联系.
o
y
x
o
y
x
y
o
x
o
y
x
下面我们利用向量法探究上述问题
探究在平面直角坐标系中,设直线l的倾斜角为
(1)已知直线l经过O(0,0),P( ,1), 与O,P的坐标有什么关系?
(2)类似地,如果直线l经过P1(-1,1),P2( ,0) , 与P1,P2的坐标又有什么关系?
(3)一般地,如果直线l经过两点P1 (x1,y1) ,P2 (x2,y2) ,x1≠x2,那么 与P1,P2的坐标有怎样的关系?
学习新知
学习新知
思考 当直线P1P2与x轴平行或重合时,上述式子还成立吗?为什么?
倾斜角是90°的直线没有斜率,倾斜角不是90°的直线都有斜率.
由正切函数的单调性,倾斜角不同的直线,其斜率也不同.因此,我们可以用斜率表示倾斜角不等于90°的直线相对于x轴的倾斜程度,进而表示直线的方向.
公式的特点:
(1)与两点的顺序无关;
(2) 公式表明,直线对于x轴的倾斜度,可以通过直线上任意两点的坐标来表示,而不需要求出直线的倾斜角;
(3)当x1=x2时,公式不适用,此时直线与x轴垂直,α=900
斜率公式
思考
(1)已知直线上的两点A(a1,a2),B(b1,b2),运用上述公式计算直线AB的斜率时,与A,B两点的顺序有关吗?
(2)当直线平行于y轴,或与y轴重合时,上述公式还适用吗?为什么?
一条直线倾斜角的正切值叫做这条直线的斜率。斜率通常用k表示,即:
2、直线的斜率
思考:日常生活中,还有没有表示倾斜程度的量呢?
前进
升高
注意:
学习新知
1 、两直线的斜率相等,它们的倾斜角也相等
2 、直线斜率的范围是R
(1)当 时,k随 增大而增大,且k≥0
(2)当 时,k随 增大而增大,且k<0
1.下列哪些说法是正确的( )
A 、任一条直线都有倾斜角,也都有斜率
B、直线的倾斜角越大,斜率也越大
C 、平行于x轴的直线的倾斜角是0°或180°
D. 一定点和一倾斜角可以唯一确定一条直线
D
达标练习
l1
l2
l3
k2>k3>k1
我们知道,直线P1P2上的向量 以及与它平行的向量都是直线的方向向量.直线P1P2的方向向量 的坐标为
例1 如下图,已知A(3,2),B(-4,1),C(0,-1),求直线AB,BC,CA的斜率,并判断这些直线的倾斜角是锐角还是纯角.
O
x
y
A
C
B
锐角
钝角
锐角
(2).过点C的直线l与线段AB有公共点,求l的斜率k的取值范围
典型例题
例2、在平面直角坐标系中,画出经过原点且斜率分别为1,-1,2和-3的直线 。
O
x
y
A3
A1
A2
A4
典型例题
1:直线的倾斜角的概念
2:直线的斜率
3:斜率公式
课堂小结
4:y=tanx的图象
