2.2.2直线的两点式方程 课件(共20张PPT)
文档属性
| 名称 | 2.2.2直线的两点式方程 课件(共20张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 768.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-29 00:00:00 | ||
图片预览






文档简介
(共20张PPT)
第二章 直线和圆的方程
2.2.2直线的两点式方程
1.点斜式方程
当知道斜率和一点坐标时用点斜式
2.斜截式方程
当知道斜率k和截距b时用斜截式
3.特殊情况
①直线和x轴平行时,倾斜角α=0°
②直线与x轴垂直时,倾斜角α=90°
x
y
l
x
y
l
y0
l
x
y
O
x0
复习回顾
思考:
学习新知
尝试:
x
y
l
P2(x2,y2)
P1(x1,y1)
【排忧解惑】
直线方程的两点式:
学习新知
讨论:两点式方程不适用于什么直线?
直线方程的两点式:
若点P1 ( x1 , y1 ),P2( x2 , y2)中有x1 =x2或y1= y2,此时过这两点的直线方程是什么?
当x1 =x2 时方程为: x =x1
当 y1= y2 时方程为: y= y1
学习新知
已知两点坐标,求直线方程的方法:
①用两点式
②先求出斜率k,再用斜截式。
小结:
练习:
课本第64页练习1
学习新知
x
y
A(-5,0)
C(0,2)
B(3,-3)
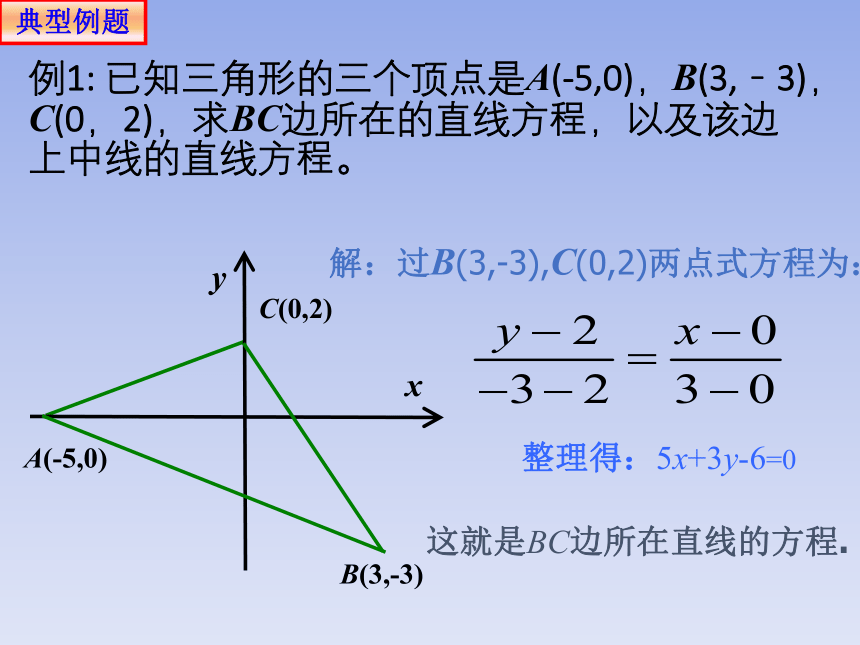
例1: 已知三角形的三个顶点是A(-5,0),B(3,-3),C(0,2),求BC边所在的直线方程,以及该边上中线的直线方程。
解:过B(3,-3),C(0,2)两点式方程为:
整理得:5x+3y-6=0
这就是BC边所在直线的方程.
典型例题
x
y
A(-5,0)
M(xM,yM)
中点
C(0,2)
B(3,-3)
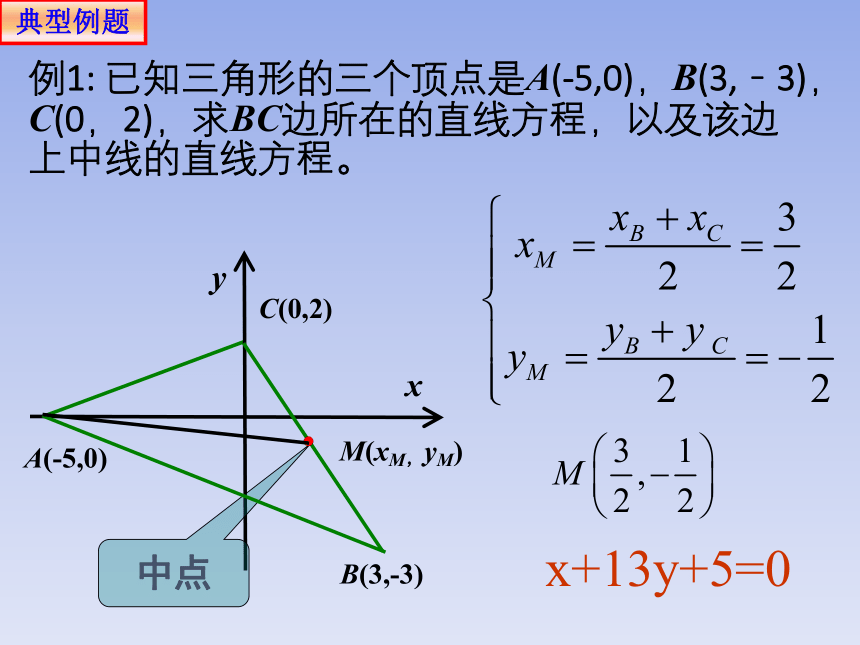
x+13y+5=0
典型例题
例1: 已知三角形的三个顶点是A(-5,0),B(3,-3),C(0,2),求BC边所在的直线方程,以及该边上中线的直线方程。
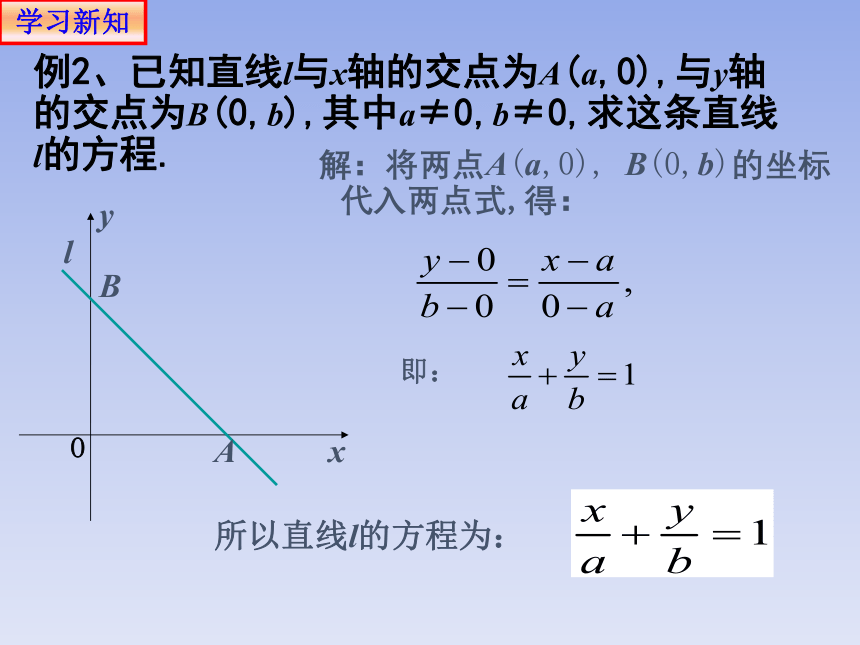
解:将两点A(a,0), B(0,b)的坐标代入两点式,得:
即:
所以直线l的方程为:
例2、已知直线l与x轴的交点为A(a,0),与y轴的交点为B(0,b),其中a≠0,b≠0,求这条直线l的方程.
x
l
B
A
O
y
学习新知
x
l
A(a,0)
B(0,b)
a为直线在x轴上的截距
b为直线在y轴上的截距
学习新知
y
O
截距式方程:
不能表示过原点或与坐标轴平行或重合的直线
讨论:
是不是任意一条直线都有截距式方程呢?
学习新知
截距式方程:
巩固练习
B
过(1,2)并且在两个坐标轴上的截距相等的直线有几条
解: ⑴ 两条
那还有一条呢?
y=2x (与x轴和y轴的截距都为0)
所以直线方程为:x+y-3=0
即:a=3
把(1,2)代入得:
设 直线的方程为:
巩固练习
解:三条
⑵ 过(1,2)并且在两个坐标轴上的截距的
绝对值相等的直线有几条
解得:a=b=3或a=-b=-1
直线方程为:y+x-3=0、y-x-1=0或y=2x
设
练习课本第64页练习2,3
巩固练习
过点P(1,3),且与x轴、y轴的正半轴围成的三角形的面积等于6的直线方程是( )
A.3x+y-6=0 B.x+3y-10=0 C.3x-y=0 D.x-3y+8=0
巩固练习
总结归纳:在涉及直线与两个坐标轴的截距问题时,常把直线方程设为截距式,由已知条件建立关于两截距的方程,解得截距的值,从而确定方程.
1.已知△ABC三顶点A(1,2),B(3,6),C(5,2),M为AB的中点,N为AC的中点,则中位线MN所在的直线方程为( )
A.2x+y-8=0 B.2x-y+8=0 C.2x+y-12=0 D.2x-y-12=0
巩固练习
A
2.直线ax+by=1(ab≠0)与两坐标轴围成的三角形的面积是 .
如图,某小区内有一块荒地ABCDE,已知BC=210 m,CD=240 m,DE=300 m,EA=180 m,AE∥CD,BC∥DE,∠C=90°,今欲在该荒地上划出一块长方形地面(不改变方位)进行开发.问如何设计才能使开发的面积最大 最大开发面积是多少
应用数学
如图,某小区内有一块荒地ABCDE,已知BC=210 m,CD=240 m,DE=300 m,EA=180 m,AE∥CD,BC∥DE,∠C=90°,今欲在该荒地上划出一块长方形地面(不改变方位)进行开发.问如何设计才能使开发的面积最大 最大开发面积是多少
应用数学
点斜式
斜率和一点坐标
斜截式
斜率k和截距b
两点坐标
两点式
点斜式
两个截距
截距式
知识小结
Thank you for watching !
第二章 直线和圆的方程
2.2.2直线的两点式方程
1.点斜式方程
当知道斜率和一点坐标时用点斜式
2.斜截式方程
当知道斜率k和截距b时用斜截式
3.特殊情况
①直线和x轴平行时,倾斜角α=0°
②直线与x轴垂直时,倾斜角α=90°
x
y
l
x
y
l
y0
l
x
y
O
x0
复习回顾
思考:
学习新知
尝试:
x
y
l
P2(x2,y2)
P1(x1,y1)
【排忧解惑】
直线方程的两点式:
学习新知
讨论:两点式方程不适用于什么直线?
直线方程的两点式:
若点P1 ( x1 , y1 ),P2( x2 , y2)中有x1 =x2或y1= y2,此时过这两点的直线方程是什么?
当x1 =x2 时方程为: x =x1
当 y1= y2 时方程为: y= y1
学习新知
已知两点坐标,求直线方程的方法:
①用两点式
②先求出斜率k,再用斜截式。
小结:
练习:
课本第64页练习1
学习新知
x
y
A(-5,0)
C(0,2)
B(3,-3)
例1: 已知三角形的三个顶点是A(-5,0),B(3,-3),C(0,2),求BC边所在的直线方程,以及该边上中线的直线方程。
解:过B(3,-3),C(0,2)两点式方程为:
整理得:5x+3y-6=0
这就是BC边所在直线的方程.
典型例题
x
y
A(-5,0)
M(xM,yM)
中点
C(0,2)
B(3,-3)
x+13y+5=0
典型例题
例1: 已知三角形的三个顶点是A(-5,0),B(3,-3),C(0,2),求BC边所在的直线方程,以及该边上中线的直线方程。
解:将两点A(a,0), B(0,b)的坐标代入两点式,得:
即:
所以直线l的方程为:
例2、已知直线l与x轴的交点为A(a,0),与y轴的交点为B(0,b),其中a≠0,b≠0,求这条直线l的方程.
x
l
B
A
O
y
学习新知
x
l
A(a,0)
B(0,b)
a为直线在x轴上的截距
b为直线在y轴上的截距
学习新知
y
O
截距式方程:
不能表示过原点或与坐标轴平行或重合的直线
讨论:
是不是任意一条直线都有截距式方程呢?
学习新知
截距式方程:
巩固练习
B
过(1,2)并且在两个坐标轴上的截距相等的直线有几条
解: ⑴ 两条
那还有一条呢?
y=2x (与x轴和y轴的截距都为0)
所以直线方程为:x+y-3=0
即:a=3
把(1,2)代入得:
设 直线的方程为:
巩固练习
解:三条
⑵ 过(1,2)并且在两个坐标轴上的截距的
绝对值相等的直线有几条
解得:a=b=3或a=-b=-1
直线方程为:y+x-3=0、y-x-1=0或y=2x
设
练习课本第64页练习2,3
巩固练习
过点P(1,3),且与x轴、y轴的正半轴围成的三角形的面积等于6的直线方程是( )
A.3x+y-6=0 B.x+3y-10=0 C.3x-y=0 D.x-3y+8=0
巩固练习
总结归纳:在涉及直线与两个坐标轴的截距问题时,常把直线方程设为截距式,由已知条件建立关于两截距的方程,解得截距的值,从而确定方程.
1.已知△ABC三顶点A(1,2),B(3,6),C(5,2),M为AB的中点,N为AC的中点,则中位线MN所在的直线方程为( )
A.2x+y-8=0 B.2x-y+8=0 C.2x+y-12=0 D.2x-y-12=0
巩固练习
A
2.直线ax+by=1(ab≠0)与两坐标轴围成的三角形的面积是 .
如图,某小区内有一块荒地ABCDE,已知BC=210 m,CD=240 m,DE=300 m,EA=180 m,AE∥CD,BC∥DE,∠C=90°,今欲在该荒地上划出一块长方形地面(不改变方位)进行开发.问如何设计才能使开发的面积最大 最大开发面积是多少
应用数学
如图,某小区内有一块荒地ABCDE,已知BC=210 m,CD=240 m,DE=300 m,EA=180 m,AE∥CD,BC∥DE,∠C=90°,今欲在该荒地上划出一块长方形地面(不改变方位)进行开发.问如何设计才能使开发的面积最大 最大开发面积是多少
应用数学
点斜式
斜率和一点坐标
斜截式
斜率k和截距b
两点坐标
两点式
点斜式
两个截距
截距式
知识小结
Thank you for watching !
