2.2.3直线的一般式式方程 课件(共21张PPT)
文档属性
| 名称 | 2.2.3直线的一般式式方程 课件(共21张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-29 00:00:00 | ||
图片预览







文档简介
(共21张PPT)
第二章 直线和圆的方程
2.2.3直线的一般式式方程
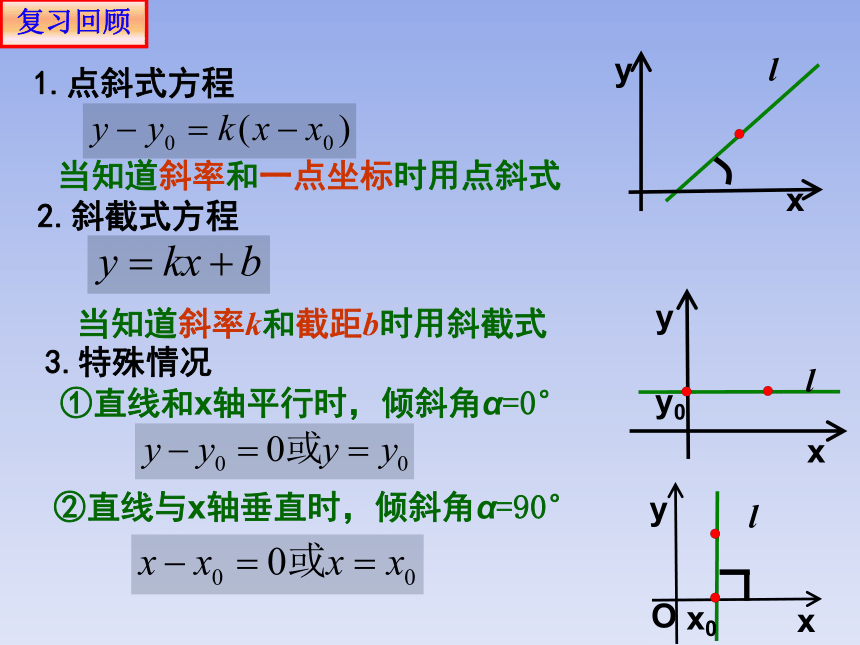
1.点斜式方程
当知道斜率和一点坐标时用点斜式
2.斜截式方程
当知道斜率k和截距b时用斜截式
3.特殊情况
①直线和x轴平行时,倾斜角α=0°
②直线与x轴垂直时,倾斜角α=90°
x
y
l
x
y
l
y0
l
x
y
O
x0
复习回顾
两点式方程不适用于什么直线?
当直线没有斜率或斜率为0时,即平行于坐标轴或与坐标轴重合的直线不能用两点式求出它们的方程。
直线方程的两点式:
当x1 =x2 时方程为:x =x1
当 y1= y2时方程为:y= y1
截距式方程:
不能表示过原点和与坐标轴平行或重合的直线
复习回顾
思考1:直线的点斜式、斜截式、两点式、截距式方程都是关于x,y的方程,这些方程所属的类型是什么?
思考2:二元一次方程的一般形式是什么?
Ax+By+C=0
直线方程的一般式
学习新知
二元一次方程
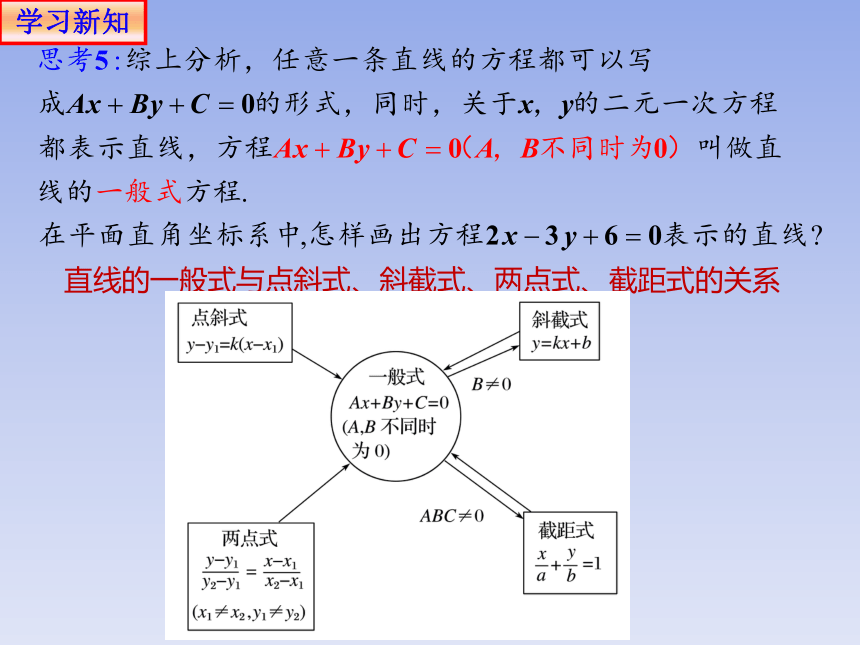
思考3:平面直角坐标系中的任意一条直线方程都可以写成Ax+By+C=0的形式吗?
思考4:关于x,y的二元一次方程Ax+By+C=0
(A,B不同时为0),
当B=0时,方程表示的图形是什么?
当B≠0时,方程表示的图形是什么?
学习新知
平行于y轴或与y轴重合的直线
学习新知
直线的一般式与点斜式、斜截式、两点式、截距式的关系
直线的一般式方程:
(1)平行于x轴 ____________
(2)平行于y轴 ____________
(3)与x轴重合 ____________
(4)与y轴重合 ____________
学习新知
探究:
典型例题
典型例题
我们可以从几何角度看一个二元一次方程即一个二元一次方程表示一条直线.
在代数中,我们研究了二元一次方程的解,因为二元一次方程的每一组解都可以看成平面直角坐标系中一个点的坐标,所以这个方程的全体解组成的集合,就是坐标满足二元一次方程的全体点的集合,这些点的集合组成一条直线.
平面直角坐标系是把二元一次方程和直线联系起来的桥梁,这是笛卡儿的伟大贡献。在平面直角坐标系中,任意一个二元一次方程是直角坐标平面上一条确定的直线;反之,直角坐标平面上的任意一条直线可以用一个确定的二元一次方程表示.
学习新知
例3 设直线l的方程为(m2-2m-3)x-(2m2+m-1)y+6-2m=0.
(1)若直线l在x轴上的截距为-3,则m=________.
(2)若直线l的斜率为1,则m=________.
典型例题
(1)方程Ax+By+C=0表示直线,需满足A,B不同时为0.
(2)令x=0可得在y轴上的截距.
令y=0可得在x轴上的截距.
若确定直线斜率存在,可将一般式化为斜截式.
(3)解分式方程注意验根.
方法总结
例4 判断下列直线的位置关系:
(1)l1:2x-3y+4=0,l2:3y-2x+4=0;
(2)l1:2x-3y+4=0,l2:-4x+6y-8=0;
典型例题
(3)l1:(-a-1)x+y=5,l2:2x+(2a+2)y+4=0.
典型例题
解 由题意知,当a=-1时,
l1:y=5,l2:x+2=0,∴l1⊥l2.
当a≠-1时,故l1不平行于l2,
又(-a-1)×2+(2a+2)×1=0,
∴l1⊥l2,综上l1⊥l2.
(1)当直线方程中存在字母参数时,不仅要考虑到斜率存在的一般情况,也要考虑到斜率不存在的特殊情况.同时还要注意x、y的系数不能同时为零这一隐含条件.
方法小结
直线l1:A1x+B1y+C1=0和直线l2:A2x+B2y+C2=0
(2)在判断两直线平行、垂直时,也可直接利用直线方程的系数间的关系得出结论.
巩固练习
a≠-2
方法二
巩固练习
巩固练习
巩固练习
巩固练习
Thank you for watching !
第二章 直线和圆的方程
2.2.3直线的一般式式方程
1.点斜式方程
当知道斜率和一点坐标时用点斜式
2.斜截式方程
当知道斜率k和截距b时用斜截式
3.特殊情况
①直线和x轴平行时,倾斜角α=0°
②直线与x轴垂直时,倾斜角α=90°
x
y
l
x
y
l
y0
l
x
y
O
x0
复习回顾
两点式方程不适用于什么直线?
当直线没有斜率或斜率为0时,即平行于坐标轴或与坐标轴重合的直线不能用两点式求出它们的方程。
直线方程的两点式:
当x1 =x2 时方程为:x =x1
当 y1= y2时方程为:y= y1
截距式方程:
不能表示过原点和与坐标轴平行或重合的直线
复习回顾
思考1:直线的点斜式、斜截式、两点式、截距式方程都是关于x,y的方程,这些方程所属的类型是什么?
思考2:二元一次方程的一般形式是什么?
Ax+By+C=0
直线方程的一般式
学习新知
二元一次方程
思考3:平面直角坐标系中的任意一条直线方程都可以写成Ax+By+C=0的形式吗?
思考4:关于x,y的二元一次方程Ax+By+C=0
(A,B不同时为0),
当B=0时,方程表示的图形是什么?
当B≠0时,方程表示的图形是什么?
学习新知
平行于y轴或与y轴重合的直线
学习新知
直线的一般式与点斜式、斜截式、两点式、截距式的关系
直线的一般式方程:
(1)平行于x轴 ____________
(2)平行于y轴 ____________
(3)与x轴重合 ____________
(4)与y轴重合 ____________
学习新知
探究:
典型例题
典型例题
我们可以从几何角度看一个二元一次方程即一个二元一次方程表示一条直线.
在代数中,我们研究了二元一次方程的解,因为二元一次方程的每一组解都可以看成平面直角坐标系中一个点的坐标,所以这个方程的全体解组成的集合,就是坐标满足二元一次方程的全体点的集合,这些点的集合组成一条直线.
平面直角坐标系是把二元一次方程和直线联系起来的桥梁,这是笛卡儿的伟大贡献。在平面直角坐标系中,任意一个二元一次方程是直角坐标平面上一条确定的直线;反之,直角坐标平面上的任意一条直线可以用一个确定的二元一次方程表示.
学习新知
例3 设直线l的方程为(m2-2m-3)x-(2m2+m-1)y+6-2m=0.
(1)若直线l在x轴上的截距为-3,则m=________.
(2)若直线l的斜率为1,则m=________.
典型例题
(1)方程Ax+By+C=0表示直线,需满足A,B不同时为0.
(2)令x=0可得在y轴上的截距.
令y=0可得在x轴上的截距.
若确定直线斜率存在,可将一般式化为斜截式.
(3)解分式方程注意验根.
方法总结
例4 判断下列直线的位置关系:
(1)l1:2x-3y+4=0,l2:3y-2x+4=0;
(2)l1:2x-3y+4=0,l2:-4x+6y-8=0;
典型例题
(3)l1:(-a-1)x+y=5,l2:2x+(2a+2)y+4=0.
典型例题
解 由题意知,当a=-1时,
l1:y=5,l2:x+2=0,∴l1⊥l2.
当a≠-1时,故l1不平行于l2,
又(-a-1)×2+(2a+2)×1=0,
∴l1⊥l2,综上l1⊥l2.
(1)当直线方程中存在字母参数时,不仅要考虑到斜率存在的一般情况,也要考虑到斜率不存在的特殊情况.同时还要注意x、y的系数不能同时为零这一隐含条件.
方法小结
直线l1:A1x+B1y+C1=0和直线l2:A2x+B2y+C2=0
(2)在判断两直线平行、垂直时,也可直接利用直线方程的系数间的关系得出结论.
巩固练习
a≠-2
方法二
巩固练习
巩固练习
巩固练习
巩固练习
Thank you for watching !
