2.3.4两条平行直线间的距离 课件(共18张PPT)
文档属性
| 名称 | 2.3.4两条平行直线间的距离 课件(共18张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-29 12:43:24 | ||
图片预览






文档简介
(共18张PPT)
第二章 直线和圆的方程
2.3.4两条平行直线间的距离
P0(x0,y0)到直线l:Ax+By+C=0的距离:
(1)分子是P点坐标代入直线方程;
(2)分母是直线未知数x、y系数平方和的算术根
类似于勾股定理求斜边的长
回顾引入
(4)当点P0在直线l上时,点到直线的距离为零,公式仍然适用.
(3)运用此公式时要注意直线方程必须是一般式,
若给出其他形式,应先化成一般式再用公式.
新课引入
A.两平行线的距离 B.点到直线的距离 C. 点到点的距离
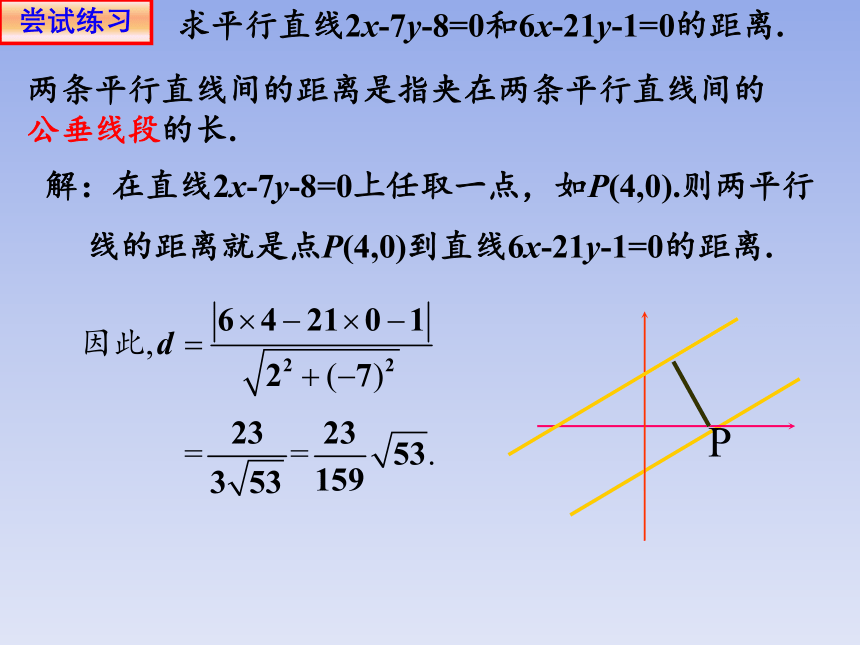
求平行直线2x-7y-8=0和6x-21y-1=0的距离.
解:在直线2x-7y-8=0上任取一点,如P(4,0).则两平行线的距离就是点P(4,0)到直线6x-21y-1=0的距离.
P
尝试练习
两条平行直线间的距离是指夹在两条平行直线间的公垂线段的长.
两条平行直线的距离是否有公式可以推出呢?
求两条平行直线Ax+By+C1=0与Ax+By+C2=0的距离.
两条平行直线间的距离是指夹在两条平行直线间的公垂线段的长.
y
x
o
l2
l1
Q
P
学习新知
解:在直线上Ax+By+C1=0任取一点,如P(x0,y0).
则两平行线的距离就是点P(x0, y0)
到直线Ax+By+C2=0 的距离.(如图)
两条平行直线间的距离:
则它们之间的距离为:
学习新知
注意
(1)把直线方程化为直线的一般式方程;
(2)两条直线方程中x,y的系数必须分别相等;
(3)两平行线间的距离是一条直线上任一点到另一条直线的距离,也可以看作是两条直线上各取一点的最短距离.
例1(1) 已知两平行直线l1:3x+5y+1=0和l2:6x+10y+5=0,则l1与l2间的距离为 .
(2) 直线3x+y-3=0和直线6x+my-1=0平行,则它们之间的距离为 .
典型例题
(3) 已知直线l与两直线l1:2x-y+3=0和l2:2x-y-1=0间的距离相等,则直线l的方程为 .
典型例题
典例解析
例2.两条互相平行的直线分别过点A(6,2)和B(-3,-1),并且各自绕着A,B旋转,如果两条平行直线间的距离为d.你能求出d的取值范围吗?
变式:上述问题中,当d取最大值时,请求出两条直线的方程.
典例解析
典型例题
思路探究:由题设知l1∥l2,故l∥l1∥l2,设出l的方程,利用距离公式表示出d1,d2.进而求出直线方程.
归纳总结
1.若直线l1:x+my+6=0与l2:(m-2)x+3y+2m=0互相平行,则m的值为 ,它们之间的距离为 .
巩固练习
2.已知直线l1,l2是分别经过A(1,1),B(0,-1)两点的两条平行直线,当l1,l2间的距离最大时,直线l1的方程是 .
x+2y-3=0.
3.直线l1过点A(0,1),l2过点B(5,0),如果l1∥l2,且l1与l2间的距离为5,求l1,l2的方程.
巩固练习
归纳总结
距离公式综合应用的三种常用类型
(1)最值问题.
利用对称转化为两点之间的距离问题.
利用所求式子的几何意义转化为点到直线的距离.
利用距离公式将问题转化为一元二次函数的最值问题,通过配方求最值.
(2)求参数问题.
利用距离公式建立关于参数的方程或方程组,通过解方程或方程组求值.
(3)求方程的问题.
立足确定直线的几何要素——点和方向,利用直线方程的各种形式,结合直线的位置关系(平行直线系、垂直直线系及过交点的直线系),巧设直线方程,在此基础上借助三种距离公式求解.)
典型例题
归纳总结
一束光线从原点O(0,0)出发,经过直线l:8x+6y=25反射后通过点P(-4,3),求反射光线的方程.
巩固练习
解 设原点关于l的对称点A的坐标为(a,b),
由直线OA与l垂直和线段AO的中点在l上得
∴A的坐标为(4,3).
∵反射光线的反向延长线过A(4,3),又由反射光线过P(-4,3),
两点纵坐标相等,故反射光线所在直线方程为y=3.
Thank you for watching !
第二章 直线和圆的方程
2.3.4两条平行直线间的距离
P0(x0,y0)到直线l:Ax+By+C=0的距离:
(1)分子是P点坐标代入直线方程;
(2)分母是直线未知数x、y系数平方和的算术根
类似于勾股定理求斜边的长
回顾引入
(4)当点P0在直线l上时,点到直线的距离为零,公式仍然适用.
(3)运用此公式时要注意直线方程必须是一般式,
若给出其他形式,应先化成一般式再用公式.
新课引入
A.两平行线的距离 B.点到直线的距离 C. 点到点的距离
求平行直线2x-7y-8=0和6x-21y-1=0的距离.
解:在直线2x-7y-8=0上任取一点,如P(4,0).则两平行线的距离就是点P(4,0)到直线6x-21y-1=0的距离.
P
尝试练习
两条平行直线间的距离是指夹在两条平行直线间的公垂线段的长.
两条平行直线的距离是否有公式可以推出呢?
求两条平行直线Ax+By+C1=0与Ax+By+C2=0的距离.
两条平行直线间的距离是指夹在两条平行直线间的公垂线段的长.
y
x
o
l2
l1
Q
P
学习新知
解:在直线上Ax+By+C1=0任取一点,如P(x0,y0).
则两平行线的距离就是点P(x0, y0)
到直线Ax+By+C2=0 的距离.(如图)
两条平行直线间的距离:
则它们之间的距离为:
学习新知
注意
(1)把直线方程化为直线的一般式方程;
(2)两条直线方程中x,y的系数必须分别相等;
(3)两平行线间的距离是一条直线上任一点到另一条直线的距离,也可以看作是两条直线上各取一点的最短距离.
例1(1) 已知两平行直线l1:3x+5y+1=0和l2:6x+10y+5=0,则l1与l2间的距离为 .
(2) 直线3x+y-3=0和直线6x+my-1=0平行,则它们之间的距离为 .
典型例题
(3) 已知直线l与两直线l1:2x-y+3=0和l2:2x-y-1=0间的距离相等,则直线l的方程为 .
典型例题
典例解析
例2.两条互相平行的直线分别过点A(6,2)和B(-3,-1),并且各自绕着A,B旋转,如果两条平行直线间的距离为d.你能求出d的取值范围吗?
变式:上述问题中,当d取最大值时,请求出两条直线的方程.
典例解析
典型例题
思路探究:由题设知l1∥l2,故l∥l1∥l2,设出l的方程,利用距离公式表示出d1,d2.进而求出直线方程.
归纳总结
1.若直线l1:x+my+6=0与l2:(m-2)x+3y+2m=0互相平行,则m的值为 ,它们之间的距离为 .
巩固练习
2.已知直线l1,l2是分别经过A(1,1),B(0,-1)两点的两条平行直线,当l1,l2间的距离最大时,直线l1的方程是 .
x+2y-3=0.
3.直线l1过点A(0,1),l2过点B(5,0),如果l1∥l2,且l1与l2间的距离为5,求l1,l2的方程.
巩固练习
归纳总结
距离公式综合应用的三种常用类型
(1)最值问题.
利用对称转化为两点之间的距离问题.
利用所求式子的几何意义转化为点到直线的距离.
利用距离公式将问题转化为一元二次函数的最值问题,通过配方求最值.
(2)求参数问题.
利用距离公式建立关于参数的方程或方程组,通过解方程或方程组求值.
(3)求方程的问题.
立足确定直线的几何要素——点和方向,利用直线方程的各种形式,结合直线的位置关系(平行直线系、垂直直线系及过交点的直线系),巧设直线方程,在此基础上借助三种距离公式求解.)
典型例题
归纳总结
一束光线从原点O(0,0)出发,经过直线l:8x+6y=25反射后通过点P(-4,3),求反射光线的方程.
巩固练习
解 设原点关于l的对称点A的坐标为(a,b),
由直线OA与l垂直和线段AO的中点在l上得
∴A的坐标为(4,3).
∵反射光线的反向延长线过A(4,3),又由反射光线过P(-4,3),
两点纵坐标相等,故反射光线所在直线方程为y=3.
Thank you for watching !
