2.3.3点到直线的距离公式 课件(共28张PPT)
文档属性
| 名称 | 2.3.3点到直线的距离公式 课件(共28张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-29 12:44:11 | ||
图片预览






文档简介
(共28张PPT)
2.3.3点到直线的距离公式
俗话说的好,要想富先修路!某村在公路附近有一家养鸡场,现在需要铺设一条连接鸡场和主公路的道路.请同学们帮助设计一下:在理论上怎样铺路可以使这条连接道路的长度最短呢
创设问题情境
创设问题情境
点P
直线l
x
y
0
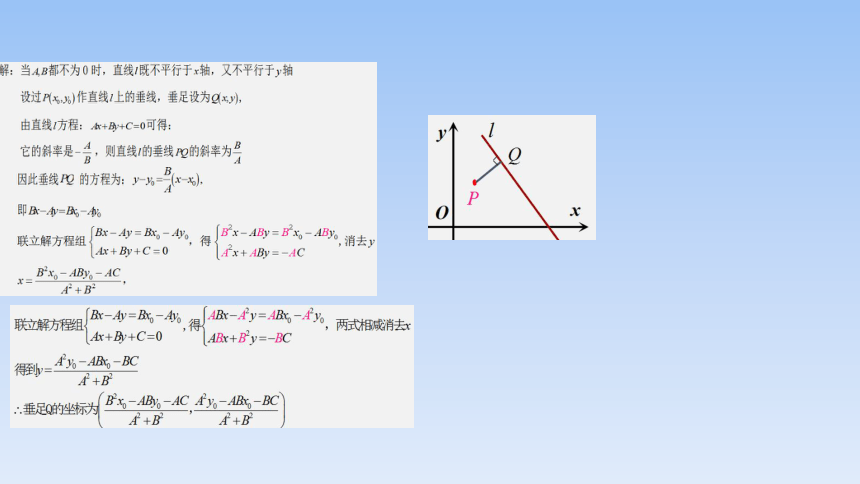
问题2: 已知任意点 ,直线 ,如何求点 到直线 的距离?
x
y
O
合作探究
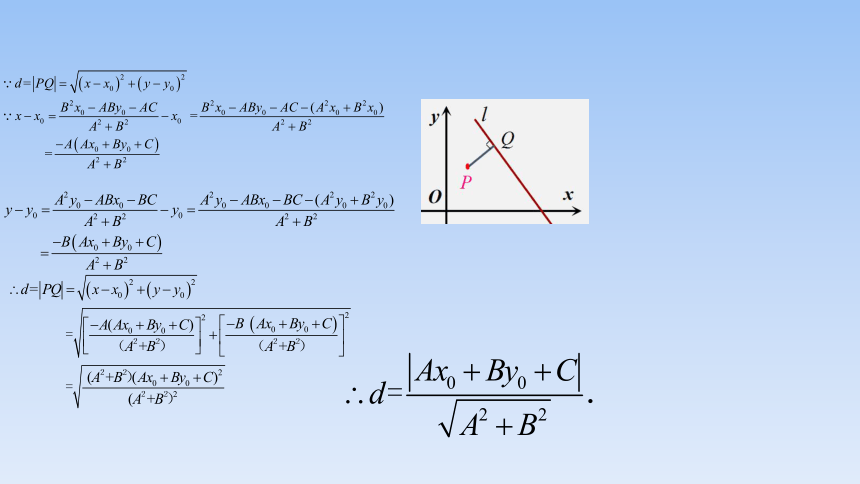
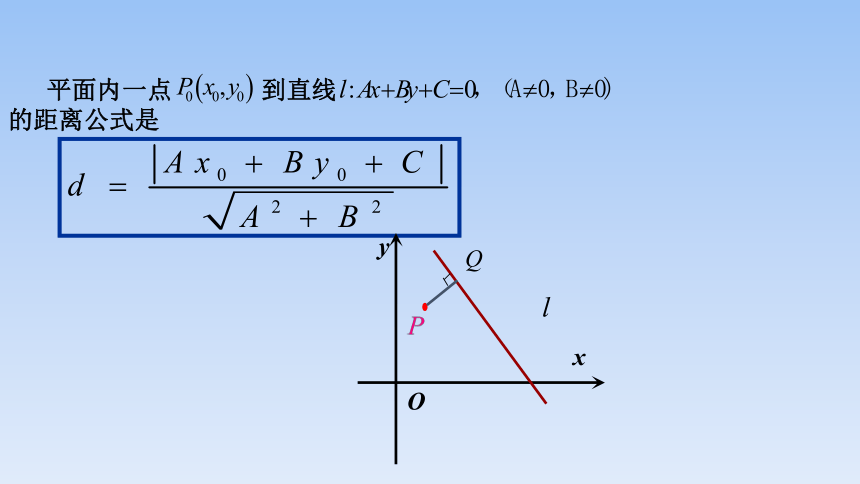
平面内一点 到直线 的距离公式是
x
y
O
Q
x
y
o
P(x0,y0)
( , y0)
Q
y
o
(x0,y0)
x
P
(x0, )
结论:当A=0或B=0,此公式也成立。
平面内一点 到直线 的距离公式是
问题3:上述推导过程比较自然,但运算较为繁杂,你认为引起复杂运算的原因是什么呢?
能否借助公式 思考怎么才能简化过程?
设而不求
整体代入
问题4:公式 在向量那章中,表示的几何意义是什么呢?可以用这个工具来推导点到直线的距离公式吗?
x
O
y
问题4:公式 在向量那章中,表示的几何意义是什么呢?可以用这个工具来推导点到直线的距离吗?
x
O
y
问题4:公式 在向量那章中,表示的几何意义是什么呢?可以用这个工具来推导点到直线的距离吗?
x
O
y
推导如下:
x
O
y
x
O
y
问题5:比较一下推导公式用的坐标法和向量法,它们各有什么特点?
坐标法:去寻求所求量的坐标表示,然后进行代数计算,整体计算量大,我们可以通过整体代换,设而不求简化一些计算,这种方法思路自然.
向量法:利用几何特征,寻找向量的坐标表示,简化了运算.
问题6:点到直线的距离公式有什么结构特征呢?
一般地,平面内一点 到直线 的距离公式是
平面内一点 到直线 的距离公式是
公式的结构特征:
分子:是将点 的坐标代入直线方程一般式的左边,得到的代数式的绝对值;
分母:是直线方程中 系数的平方和的算术平方根.
速算大比拼
0
问题7:公式使用的步骤和注意事项是什么?
公式使用步骤:
(1)找P点横纵坐标: ; ;
(3)应用公式 进行运算.
(2)的方程中找: ; ; .
使用公式时应注意的问题:
1.直线方程为一般式:直接代入计算;
2.直线方程不是一般式:先化成一般式,再代入计算;
3.直线方程:当 时,公式仍然成立,可代入公式计算,或用图形求解.
课题小结
1.我们学了公式:
3.体会到了“设而不求、整体代入”在解析几何中的简化运算作用。
2.了解到点到直线的距离公式推导方法和过程.
4.知道了应用公式有哪些注意事项.
(1) 已知直线 经过点 ,且 , 两点到
直线 的距离相等,求直线 的方程.
(2) 用解析法证明:等腰三角形底边上任意一点到两腰
的距离之和等于一腰上的高.
(3) 求经过点 ,且与原点距离等于3的直线 的方程.
(4) 已知直线过点 且与点 , 等距离,
则直线 的方程为.
(5) 直线 上到点 距离最近的点的坐标
是 .
(6) 若点 到直线 的距离不大于3,则的
取值范围是______.
作业布置及时巩固
1.必作题
2.对课堂上公式推导的方法还不清楚的学生,请观看有
关的微视频,写出推导过程.
3.选做题:收集点到直线距离公式的推导方法、撰写点
到直线距离公式的应用小论文.
2.3.3点到直线的距离公式
俗话说的好,要想富先修路!某村在公路附近有一家养鸡场,现在需要铺设一条连接鸡场和主公路的道路.请同学们帮助设计一下:在理论上怎样铺路可以使这条连接道路的长度最短呢
创设问题情境
创设问题情境
点P
直线l
x
y
0
问题2: 已知任意点 ,直线 ,如何求点 到直线 的距离?
x
y
O
合作探究
平面内一点 到直线 的距离公式是
x
y
O
Q
x
y
o
P(x0,y0)
( , y0)
Q
y
o
(x0,y0)
x
P
(x0, )
结论:当A=0或B=0,此公式也成立。
平面内一点 到直线 的距离公式是
问题3:上述推导过程比较自然,但运算较为繁杂,你认为引起复杂运算的原因是什么呢?
能否借助公式 思考怎么才能简化过程?
设而不求
整体代入
问题4:公式 在向量那章中,表示的几何意义是什么呢?可以用这个工具来推导点到直线的距离公式吗?
x
O
y
问题4:公式 在向量那章中,表示的几何意义是什么呢?可以用这个工具来推导点到直线的距离吗?
x
O
y
问题4:公式 在向量那章中,表示的几何意义是什么呢?可以用这个工具来推导点到直线的距离吗?
x
O
y
推导如下:
x
O
y
x
O
y
问题5:比较一下推导公式用的坐标法和向量法,它们各有什么特点?
坐标法:去寻求所求量的坐标表示,然后进行代数计算,整体计算量大,我们可以通过整体代换,设而不求简化一些计算,这种方法思路自然.
向量法:利用几何特征,寻找向量的坐标表示,简化了运算.
问题6:点到直线的距离公式有什么结构特征呢?
一般地,平面内一点 到直线 的距离公式是
平面内一点 到直线 的距离公式是
公式的结构特征:
分子:是将点 的坐标代入直线方程一般式的左边,得到的代数式的绝对值;
分母:是直线方程中 系数的平方和的算术平方根.
速算大比拼
0
问题7:公式使用的步骤和注意事项是什么?
公式使用步骤:
(1)找P点横纵坐标: ; ;
(3)应用公式 进行运算.
(2)的方程中找: ; ; .
使用公式时应注意的问题:
1.直线方程为一般式:直接代入计算;
2.直线方程不是一般式:先化成一般式,再代入计算;
3.直线方程:当 时,公式仍然成立,可代入公式计算,或用图形求解.
课题小结
1.我们学了公式:
3.体会到了“设而不求、整体代入”在解析几何中的简化运算作用。
2.了解到点到直线的距离公式推导方法和过程.
4.知道了应用公式有哪些注意事项.
(1) 已知直线 经过点 ,且 , 两点到
直线 的距离相等,求直线 的方程.
(2) 用解析法证明:等腰三角形底边上任意一点到两腰
的距离之和等于一腰上的高.
(3) 求经过点 ,且与原点距离等于3的直线 的方程.
(4) 已知直线过点 且与点 , 等距离,
则直线 的方程为.
(5) 直线 上到点 距离最近的点的坐标
是 .
(6) 若点 到直线 的距离不大于3,则的
取值范围是______.
作业布置及时巩固
1.必作题
2.对课堂上公式推导的方法还不清楚的学生,请观看有
关的微视频,写出推导过程.
3.选做题:收集点到直线距离公式的推导方法、撰写点
到直线距离公式的应用小论文.
