2.4.1圆的标准方程 课件(共21张PPT)
文档属性
| 名称 | 2.4.1圆的标准方程 课件(共21张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-29 12:47:12 | ||
图片预览






文档简介
(共21张PPT)
第二章 直线和圆的方程
2.4.1圆的标准方程
3.两条平行线Ax+By+C1=0与Ax+By+C2=0的距离是
2.平面内一点P(x0,y0) 到直线Ax+By+C=0的距离公式是
当A=0或B=0时,公式仍然成立.
1.两点间距离公式
复习引入
《古朗月行》
唐 李白
小时不识月,
呼作白玉盘。 又疑瑶台镜,
飞在青云端。
如果把天空看作一个平面,月亮当做一个圆,建立一个平面直角坐标系,那么圆的坐标方程如何表示
月亮,是中国人心目中的宇宙精灵,古代人们在生活中崇拜、敬畏月亮,在文学作品中也大量描写
圆的标准方程
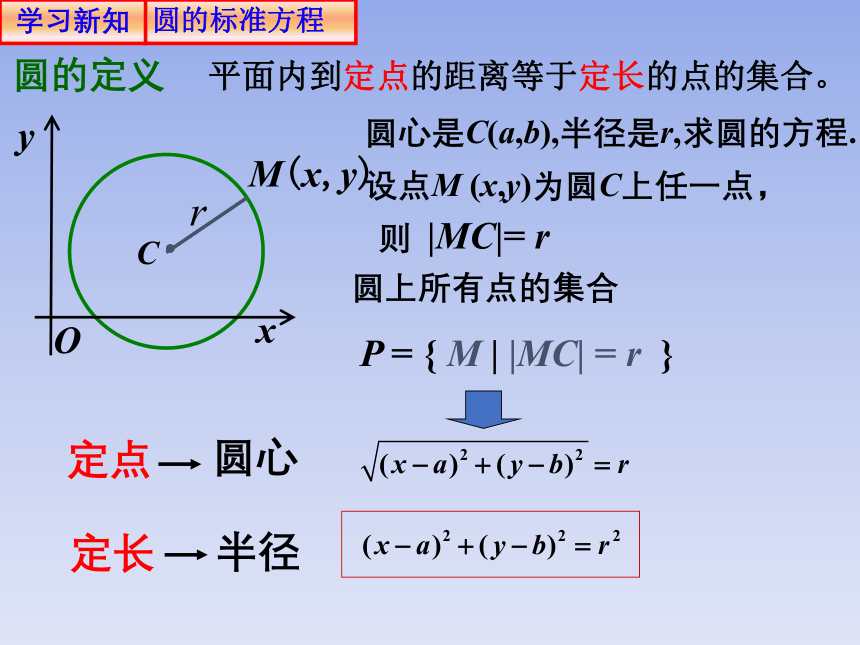
圆的定义
平面内到定点的距离等于定长的点的集合。
定点
定长
圆心
半径
·
r
C
学习新知
圆心是C(a,b),半径是r,求圆的方程.
设点M (x,y)为圆C上任一点,
x
y
O
M(x,y)
|MC|= r
则
P = { M | |MC| = r }
圆上所有点的集合
x
y
O
C
M(x,y)
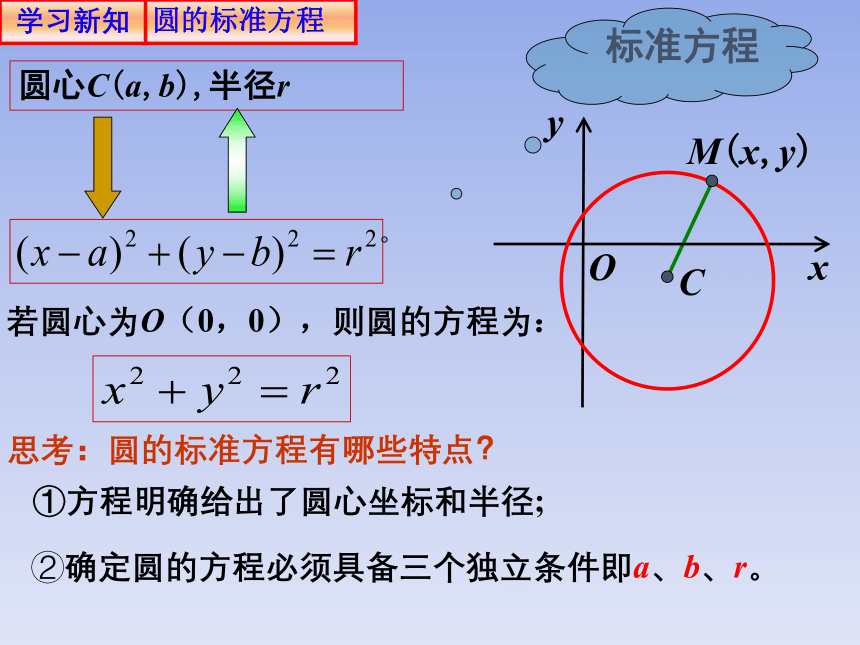
圆心C(a,b),半径r
若圆心为O(0,0),则圆的方程为:
标准方程
思考:圆的标准方程有哪些特点?
①方程明确给出了圆心坐标和半径;
②确定圆的方程必须具备三个独立条件即a、b、r。
圆的标准方程
学习新知
圆心(2,-4),半径
求下列圆的圆心和半径
⑴圆 (x-1)2+ (y-1)2=9
⑵圆 (x-2)2+ (y+4)2=2
⑶圆 (x+1)2+ (y+2)2=m2
圆心(1, 1),半径3
圆心(-1,-2),半径|m|
(4)圆x2+y2=4
(5)圆(x+1)2+y2=1
圆心(0,0)半径2
圆心(-1,0)半径1
巩固练习
典型例题
分析:根据点的坐标与圆的方程的关系,只要判断一个点的坐标是否满足圆的方程,就可以得到这个点是否在圆上.
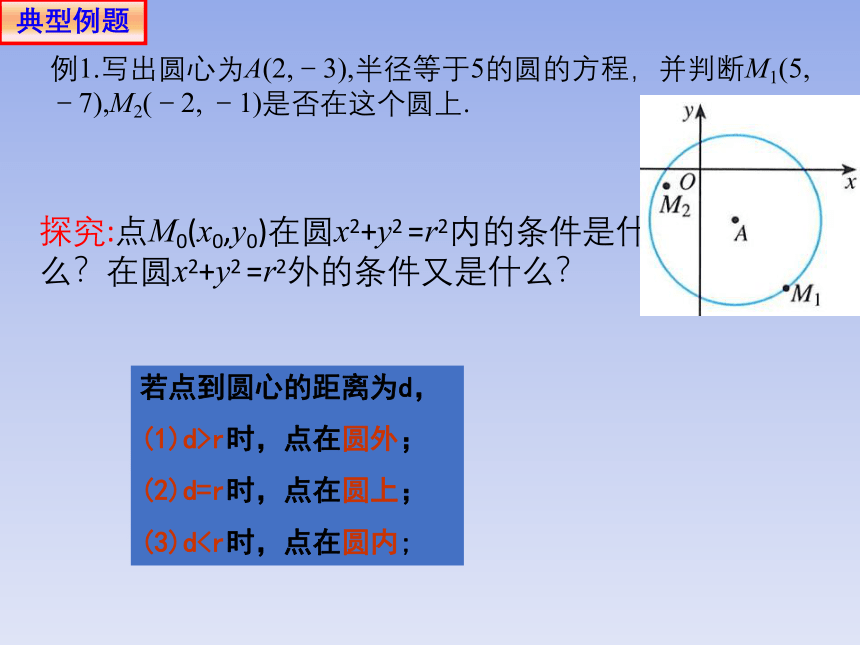
例1写出圆心为A(2,-3),半径等于5的圆的方程,并判断M1(5,-7),M2(-2, -1)是否在这个圆上.
若点到圆心的距离为d,
d>r时,点在圆外;
d=r时,点在圆上;
d典型例题
探究:点M0(x0,y0)在圆x2+y2 =r2内的条件是什么?在圆x2+y2 =r2外的条件又是什么?
例1.写出圆心为A(2,-3),半径等于5的圆的方程,并判断M1(5,-7),M2(-2, -1)是否在这个圆上.
典型例题
待定系数法
例2.△ABC的三个顶点的坐标分别是A(5,1), B(7,-3),C(2,-8),求它的外接圆方程.
待定系数法
解:设所求圆的方程为:
因为A(5,1),B (7,-3),C(2,8)都在圆上
所求圆的方程为
典型例题
例2.△ABC的三个顶点的坐标分别是A(5,1), B(7,-3),C(2,-8),求它的外接圆方程.
圆心:两条弦的中垂线的交点
半径:圆心到圆上一点
x
y
O
M
A(5,1)
B(7,-3)
C(2,-8)
法二
典型例题
例2.△ABC的三个顶点的坐标分别是A(5,1), B(7,-3),C(2,-8),求它的外接圆方程.
x
y
O
C
A(1,1)
B(2,-2)
典型例题
例3已知圆心为C的圆经过点A(1,1),B(2,-2),
且圆心C在直线l:x-y+1=0上,求圆心为C的标准方程.
圆心:两条直线的交点
半径:圆心到圆上一点
x
y
O
C
A(1,1)
B(2,-2)
弦AB的垂直平分线
典型例题
例3已知圆心为C的圆经过点A(1,1),B(2,-2),
且圆心C在直线l:x-y+1=0上,求圆心为C的标准方程.
x
y
O
C
A(1,1)
B(2,-2)
弦AB的垂直平分线
典型例题
例3已知圆心为C的圆经过点A(1,1),B(2,-2),
且圆心C在直线l:x-y+1=0上,求圆心为C的标准方程.
圆的标准方程的两种求法
(1)几何法
它是利用图形的几何性质,如圆的性质等,直接求出圆的圆心和半径,代入圆的标准方程,从而得到圆的标准方程.
方法总结
(2)待定系数法
由三个独立条件得到三个方程,解方程组以得到圆的标准方程中三个参数,从而确定圆的标准方程.它是求圆的方程最常用的方法,一般步骤是:
①设——设所求圆的方程为(x-a)2+(y-b)2=r2;
②列——由已知条件,建立关于a,b,r的方程组;
③解——解方程组,求出a,b,r;
④代——将a,b,r代入所设方程,得所求圆的方程.
巩固练习
课本P85 练习 1
课本P85 练习3
解:设点C(a,b)为直径P1P2的中点,则
圆心坐标为(5,6),
圆心:直径的中点
半径:直径的一半
圆方程为
因此点M在圆上,点N在圆外,点Q在圆内。
解:设所求圆的半径为r,则
∴所求圆的方程为
C
y
x
O
M
例4:以C(1,3)为圆心,并且和直线3x-4y-7=0相切的圆.
典型例题
典型例题
例5.若P(x,y)为圆C(x+4)2+y2=4上任意一点,请求出P(x,y)到原点的距离的最大值和最小值.
[提示] 原点到圆心C(-4,0)的距离d=4,圆的半径为2,故圆上的点到坐标原点的最大距离为4+2=6,最小距离为4-2=2.
例6.若P(x,y)是圆C(x-3)2+y2=4上任意一点,请求出P(x,y)到直线x-y+1=0的距离的最大值和最小值.
圆心C(a,b),半径r
x
y
O
C
A
B
C
1.圆的标准方程
2.圆心
①两条直线的交点(弦的垂直平分线)
②直径的中点
3.半径
①圆心到圆上一点
②圆心到切线的距离
课堂小结
作业
课本第88页第2题,第3题
课本第89页第9题
Thank you for watching !
第二章 直线和圆的方程
2.4.1圆的标准方程
3.两条平行线Ax+By+C1=0与Ax+By+C2=0的距离是
2.平面内一点P(x0,y0) 到直线Ax+By+C=0的距离公式是
当A=0或B=0时,公式仍然成立.
1.两点间距离公式
复习引入
《古朗月行》
唐 李白
小时不识月,
呼作白玉盘。 又疑瑶台镜,
飞在青云端。
如果把天空看作一个平面,月亮当做一个圆,建立一个平面直角坐标系,那么圆的坐标方程如何表示
月亮,是中国人心目中的宇宙精灵,古代人们在生活中崇拜、敬畏月亮,在文学作品中也大量描写
圆的标准方程
圆的定义
平面内到定点的距离等于定长的点的集合。
定点
定长
圆心
半径
·
r
C
学习新知
圆心是C(a,b),半径是r,求圆的方程.
设点M (x,y)为圆C上任一点,
x
y
O
M(x,y)
|MC|= r
则
P = { M | |MC| = r }
圆上所有点的集合
x
y
O
C
M(x,y)
圆心C(a,b),半径r
若圆心为O(0,0),则圆的方程为:
标准方程
思考:圆的标准方程有哪些特点?
①方程明确给出了圆心坐标和半径;
②确定圆的方程必须具备三个独立条件即a、b、r。
圆的标准方程
学习新知
圆心(2,-4),半径
求下列圆的圆心和半径
⑴圆 (x-1)2+ (y-1)2=9
⑵圆 (x-2)2+ (y+4)2=2
⑶圆 (x+1)2+ (y+2)2=m2
圆心(1, 1),半径3
圆心(-1,-2),半径|m|
(4)圆x2+y2=4
(5)圆(x+1)2+y2=1
圆心(0,0)半径2
圆心(-1,0)半径1
巩固练习
典型例题
分析:根据点的坐标与圆的方程的关系,只要判断一个点的坐标是否满足圆的方程,就可以得到这个点是否在圆上.
例1写出圆心为A(2,-3),半径等于5的圆的方程,并判断M1(5,-7),M2(-2, -1)是否在这个圆上.
若点到圆心的距离为d,
d>r时,点在圆外;
d=r时,点在圆上;
d
探究:点M0(x0,y0)在圆x2+y2 =r2内的条件是什么?在圆x2+y2 =r2外的条件又是什么?
例1.写出圆心为A(2,-3),半径等于5的圆的方程,并判断M1(5,-7),M2(-2, -1)是否在这个圆上.
典型例题
待定系数法
例2.△ABC的三个顶点的坐标分别是A(5,1), B(7,-3),C(2,-8),求它的外接圆方程.
待定系数法
解:设所求圆的方程为:
因为A(5,1),B (7,-3),C(2,8)都在圆上
所求圆的方程为
典型例题
例2.△ABC的三个顶点的坐标分别是A(5,1), B(7,-3),C(2,-8),求它的外接圆方程.
圆心:两条弦的中垂线的交点
半径:圆心到圆上一点
x
y
O
M
A(5,1)
B(7,-3)
C(2,-8)
法二
典型例题
例2.△ABC的三个顶点的坐标分别是A(5,1), B(7,-3),C(2,-8),求它的外接圆方程.
x
y
O
C
A(1,1)
B(2,-2)
典型例题
例3已知圆心为C的圆经过点A(1,1),B(2,-2),
且圆心C在直线l:x-y+1=0上,求圆心为C的标准方程.
圆心:两条直线的交点
半径:圆心到圆上一点
x
y
O
C
A(1,1)
B(2,-2)
弦AB的垂直平分线
典型例题
例3已知圆心为C的圆经过点A(1,1),B(2,-2),
且圆心C在直线l:x-y+1=0上,求圆心为C的标准方程.
x
y
O
C
A(1,1)
B(2,-2)
弦AB的垂直平分线
典型例题
例3已知圆心为C的圆经过点A(1,1),B(2,-2),
且圆心C在直线l:x-y+1=0上,求圆心为C的标准方程.
圆的标准方程的两种求法
(1)几何法
它是利用图形的几何性质,如圆的性质等,直接求出圆的圆心和半径,代入圆的标准方程,从而得到圆的标准方程.
方法总结
(2)待定系数法
由三个独立条件得到三个方程,解方程组以得到圆的标准方程中三个参数,从而确定圆的标准方程.它是求圆的方程最常用的方法,一般步骤是:
①设——设所求圆的方程为(x-a)2+(y-b)2=r2;
②列——由已知条件,建立关于a,b,r的方程组;
③解——解方程组,求出a,b,r;
④代——将a,b,r代入所设方程,得所求圆的方程.
巩固练习
课本P85 练习 1
课本P85 练习3
解:设点C(a,b)为直径P1P2的中点,则
圆心坐标为(5,6),
圆心:直径的中点
半径:直径的一半
圆方程为
因此点M在圆上,点N在圆外,点Q在圆内。
解:设所求圆的半径为r,则
∴所求圆的方程为
C
y
x
O
M
例4:以C(1,3)为圆心,并且和直线3x-4y-7=0相切的圆.
典型例题
典型例题
例5.若P(x,y)为圆C(x+4)2+y2=4上任意一点,请求出P(x,y)到原点的距离的最大值和最小值.
[提示] 原点到圆心C(-4,0)的距离d=4,圆的半径为2,故圆上的点到坐标原点的最大距离为4+2=6,最小距离为4-2=2.
例6.若P(x,y)是圆C(x-3)2+y2=4上任意一点,请求出P(x,y)到直线x-y+1=0的距离的最大值和最小值.
圆心C(a,b),半径r
x
y
O
C
A
B
C
1.圆的标准方程
2.圆心
①两条直线的交点(弦的垂直平分线)
②直径的中点
3.半径
①圆心到圆上一点
②圆心到切线的距离
课堂小结
作业
课本第88页第2题,第3题
课本第89页第9题
Thank you for watching !
