2.4.2圆的一般方程 课件(共19张PPT)
文档属性
| 名称 | 2.4.2圆的一般方程 课件(共19张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-29 12:50:23 | ||
图片预览






文档简介
(共19张PPT)
第二章 直线和圆的方程
2.4.2圆的一般方程(2)
名称 标准方程 一般方程
方程形式
圆心
半径
点A(x0,y0)在圆上
点A(x0,y0)在圆外
点A(x0,y0)在圆内
复习回顾
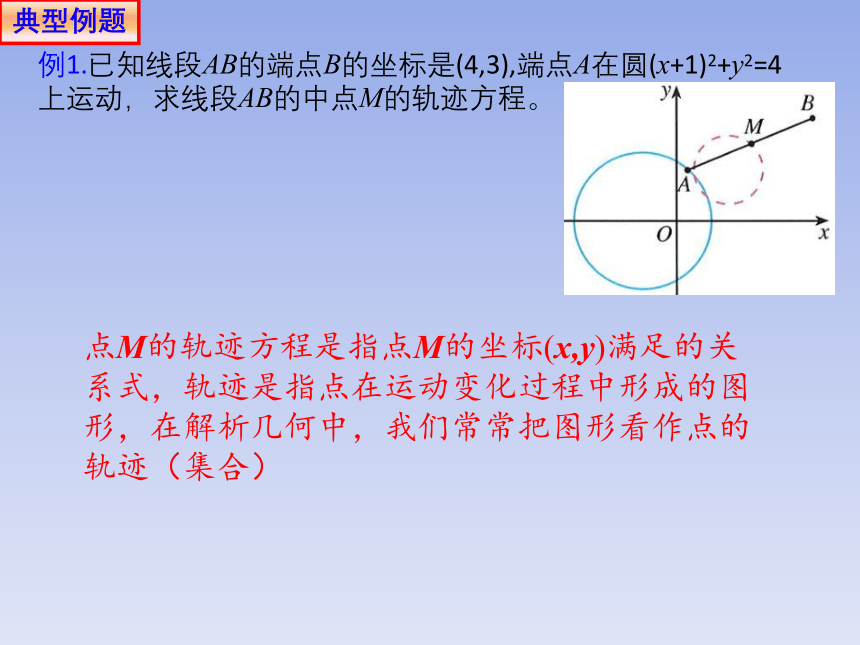
例1.已知线段AB的端点B的坐标是(4,3),端点A在圆(x+1)2+y2=4上运动,求线段AB的中点M的轨迹方程。
典型例题
例1.已知线段AB的端点B的坐标是(4,3),端点A在圆(x+1)2+y2=4上运动,求线段AB的中点M的轨迹方程。
点M的轨迹方程是指点M的坐标(x,y)满足的关系式,轨迹是指点在运动变化过程中形成的图形,在解析几何中,我们常常把图形看作点的轨迹(集合)
典型例题
例2.已知等腰三角形的顶点是A(4,2),底边一个端点是B(3,5),求另一个端点C的轨迹方程,并说明它的轨迹是什么图形.
解:设另一端点C的坐标为(x,y).依题意,得|AC|=|AB|.由两点间距离公式,得
典型例题
求动点的轨迹方程的常用方法
1.直接法:能直接根据题目提供的条件列出方程;
2.代入法:找到所求动点与已知动点的关系,代入已知动点所在的方程.
例2.已知等腰三角形的顶点是A(4,2),底边一个端点是B(3,5),求另一个端点C的轨迹方程,并说明它的轨迹是什么图形.
典型例题
变式练习:求本例中线段AC中点M的轨迹方程.
例2.已知等腰三角形的顶点是A(4,2),底边一个端点是B(3,5),求另一个端点C的轨迹方程,并说明它的轨迹是什么图形.
1.两个定点的距离为6,点M到这两个定点的距离的平方和为26,求点M的轨迹方程.
解:以两定点A,B所在直线为x轴,线段AB的中垂线为y轴,建立直角坐标系,设A(-3,0),B(3,0),M(x,y),
巩固练习
则|MA|2+|MB|2=26,
∴(x+3)2+y2+(x-3)2+y2=26,
化简得M点的轨迹方程为x2+y2=4.
巩固练习
2.已知圆(x+1)2+y2=2上动点A, x轴上定点B(2,0), 将BA延长到M,使AM=BA, 求动点M的轨迹方程.
解:设A(x1,y1),M(x,y),∵AM=BA,且M在BA的延长线上,
∴A为线段MB的中点,
典型例题
点评:当动点的变化是由某个量的变化决定的,可以设这个量为参数,用参数表示动点坐标,消去参数,就能得到动点轨迹方程.这种方法就是参数法.
典型例题
1.方程x2+y2-2x-4y+6=0表示的轨迹为( )
A.圆心为(1,2)的圆 B.圆心为(2,1)的圆
C.圆心为(-1,-2)的圆 D.不表示任何图形
解析:因为x2+y2-2x-4y+6=0等价于(x-1)2+(y-2)2=-1,即方程无解,所以该方程不表示任何图形,故选D.答案:D
2.若圆x2+y2-2kx-4=0关于直线2x-y+3=0对称,则k等于( )
B
巩固练习
3.已知一动点M到点A(-4,0)的距离是它到点B(2,0)的距离的2倍,则动点M的轨迹方程是 .
x2+y2-8x=0
巩固练习
例4.点A(2,0)是圆x2+y2=4上的定点,点B(1,1)是圆内一点,P,Q为圆上的动点.
(1)求线段AP的中点M的轨迹方程;
(2)若∠PBQ=90°,求线段PQ的中点N的轨迹方程.
典型例题
[解](1)设线段AP的中点为M(x,y),则点P坐标为(2x-2,2y).
(2)设线段PQ的中点为N(x,y),
在Rt△PBQ中,|PN|=|BN|.
设O为坐标原点,连接ON(图略),则ON⊥PQ,
∴|OP|2=|ON|2+|PN|2=|ON|2+|BN|2,
∴x2+y2+(x-1)2+(y-1)2=4,
故线段PQ的中点N的轨迹方程为x2+y2-x-y-1=0.
例4.点A(2,0)是圆x2+y2=4上的定点,点B(1,1)是圆内一点,P,Q为圆上的动点.
(1)求线段AP的中点M的轨迹方程;
(2)若∠PBQ=90°,求线段PQ的中点N的轨迹方程.
∵点P在圆x2+y2=4上,∴(2x-2)2+(2y)2=4,
∴线段AP的中点M的轨迹方程为(2x-2)2+(2y)2=4.
A
D
C
m=4时,有最小值0
2.代入法(相关点法):解决以下类型的轨迹:动点M随点A的变化而变化,而点A在某条曲线上变化,这时,设M(x,y), A(x0,y0),用x,y表示x0,y0,把x0,y0的表达式代入已知曲线的方程中,即得动点M(x,y)的轨迹方程.
1.直接法:设动点坐标,直接得出坐标所满足的关系式,而求出轨迹方程,这种求轨迹方程的方法称为直接法.
方法总结
作业
课本第88页
习题2.4第7,8, 9题
Thank you for watching !
第二章 直线和圆的方程
2.4.2圆的一般方程(2)
名称 标准方程 一般方程
方程形式
圆心
半径
点A(x0,y0)在圆上
点A(x0,y0)在圆外
点A(x0,y0)在圆内
复习回顾
例1.已知线段AB的端点B的坐标是(4,3),端点A在圆(x+1)2+y2=4上运动,求线段AB的中点M的轨迹方程。
典型例题
例1.已知线段AB的端点B的坐标是(4,3),端点A在圆(x+1)2+y2=4上运动,求线段AB的中点M的轨迹方程。
点M的轨迹方程是指点M的坐标(x,y)满足的关系式,轨迹是指点在运动变化过程中形成的图形,在解析几何中,我们常常把图形看作点的轨迹(集合)
典型例题
例2.已知等腰三角形的顶点是A(4,2),底边一个端点是B(3,5),求另一个端点C的轨迹方程,并说明它的轨迹是什么图形.
解:设另一端点C的坐标为(x,y).依题意,得|AC|=|AB|.由两点间距离公式,得
典型例题
求动点的轨迹方程的常用方法
1.直接法:能直接根据题目提供的条件列出方程;
2.代入法:找到所求动点与已知动点的关系,代入已知动点所在的方程.
例2.已知等腰三角形的顶点是A(4,2),底边一个端点是B(3,5),求另一个端点C的轨迹方程,并说明它的轨迹是什么图形.
典型例题
变式练习:求本例中线段AC中点M的轨迹方程.
例2.已知等腰三角形的顶点是A(4,2),底边一个端点是B(3,5),求另一个端点C的轨迹方程,并说明它的轨迹是什么图形.
1.两个定点的距离为6,点M到这两个定点的距离的平方和为26,求点M的轨迹方程.
解:以两定点A,B所在直线为x轴,线段AB的中垂线为y轴,建立直角坐标系,设A(-3,0),B(3,0),M(x,y),
巩固练习
则|MA|2+|MB|2=26,
∴(x+3)2+y2+(x-3)2+y2=26,
化简得M点的轨迹方程为x2+y2=4.
巩固练习
2.已知圆(x+1)2+y2=2上动点A, x轴上定点B(2,0), 将BA延长到M,使AM=BA, 求动点M的轨迹方程.
解:设A(x1,y1),M(x,y),∵AM=BA,且M在BA的延长线上,
∴A为线段MB的中点,
典型例题
点评:当动点的变化是由某个量的变化决定的,可以设这个量为参数,用参数表示动点坐标,消去参数,就能得到动点轨迹方程.这种方法就是参数法.
典型例题
1.方程x2+y2-2x-4y+6=0表示的轨迹为( )
A.圆心为(1,2)的圆 B.圆心为(2,1)的圆
C.圆心为(-1,-2)的圆 D.不表示任何图形
解析:因为x2+y2-2x-4y+6=0等价于(x-1)2+(y-2)2=-1,即方程无解,所以该方程不表示任何图形,故选D.答案:D
2.若圆x2+y2-2kx-4=0关于直线2x-y+3=0对称,则k等于( )
B
巩固练习
3.已知一动点M到点A(-4,0)的距离是它到点B(2,0)的距离的2倍,则动点M的轨迹方程是 .
x2+y2-8x=0
巩固练习
例4.点A(2,0)是圆x2+y2=4上的定点,点B(1,1)是圆内一点,P,Q为圆上的动点.
(1)求线段AP的中点M的轨迹方程;
(2)若∠PBQ=90°,求线段PQ的中点N的轨迹方程.
典型例题
[解](1)设线段AP的中点为M(x,y),则点P坐标为(2x-2,2y).
(2)设线段PQ的中点为N(x,y),
在Rt△PBQ中,|PN|=|BN|.
设O为坐标原点,连接ON(图略),则ON⊥PQ,
∴|OP|2=|ON|2+|PN|2=|ON|2+|BN|2,
∴x2+y2+(x-1)2+(y-1)2=4,
故线段PQ的中点N的轨迹方程为x2+y2-x-y-1=0.
例4.点A(2,0)是圆x2+y2=4上的定点,点B(1,1)是圆内一点,P,Q为圆上的动点.
(1)求线段AP的中点M的轨迹方程;
(2)若∠PBQ=90°,求线段PQ的中点N的轨迹方程.
∵点P在圆x2+y2=4上,∴(2x-2)2+(2y)2=4,
∴线段AP的中点M的轨迹方程为(2x-2)2+(2y)2=4.
A
D
C
m=4时,有最小值0
2.代入法(相关点法):解决以下类型的轨迹:动点M随点A的变化而变化,而点A在某条曲线上变化,这时,设M(x,y), A(x0,y0),用x,y表示x0,y0,把x0,y0的表达式代入已知曲线的方程中,即得动点M(x,y)的轨迹方程.
1.直接法:设动点坐标,直接得出坐标所满足的关系式,而求出轨迹方程,这种求轨迹方程的方法称为直接法.
方法总结
作业
课本第88页
习题2.4第7,8, 9题
Thank you for watching !
