2.5.1直线与圆的位置关系 课件(共25张PPT)
文档属性
| 名称 | 2.5.1直线与圆的位置关系 课件(共25张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-29 12:52:45 | ||
图片预览








文档简介
(共25张PPT)
第二章 直线和圆的方程
2.5 直线与圆、圆与圆的位置关系
2.5.1 直线与圆的位置关系
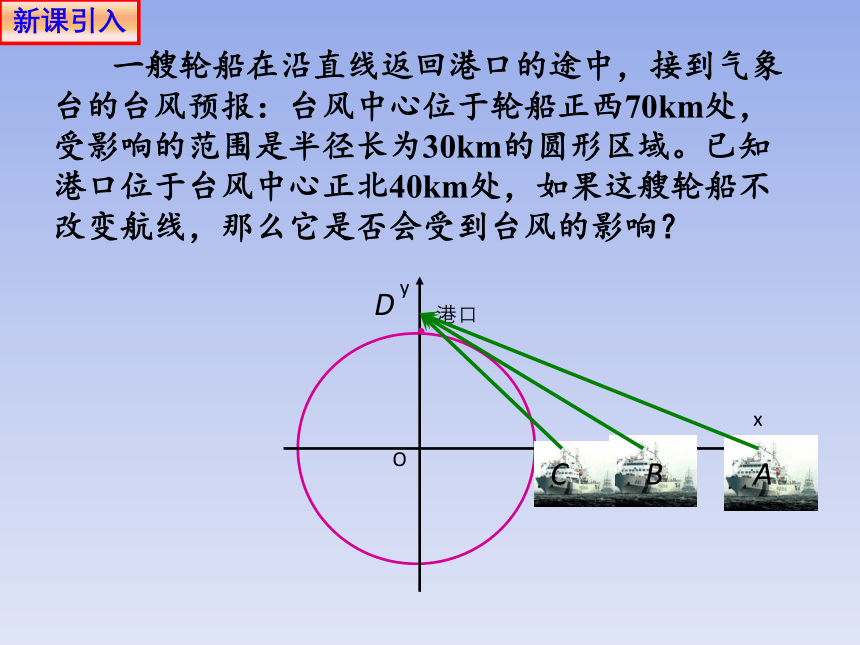
一艘轮船在沿直线返回港口的途中,接到气象台的台风预报:台风中心位于轮船正西70km处,受影响的范围是半径长为30km的圆形区域。已知港口位于台风中心正北40km处,如果这艘轮船不改变航线,那么它是否会受到台风的影响?
.
x
O
y
港口
B
C
A
D
新课引入
复习回顾
名称
方程的形式
已知条件
方程直线的局限性
一般式
点斜式
斜截式
两点式
截距式
(x1,y1)是直线上一点,k是斜率
k是斜率,b是直线在y轴上的截距
不包括与x轴垂直的直线
a是直线在x轴上的截距,b是直线在y轴上的截距
(x1,y1),(x2,y2)是直线上两点
不包括与x轴垂直的直线
不包括与坐标轴垂直的直线
A、B、C为常数
任何位置的直线
不包括与坐标轴垂直的直线,不包括过原点的直线
Ax+By+C=0
(A、B不同时为零)
直线方程的五种形式
名称 标准方程 一般方程
方程形式
圆心
半径
点A(x0,y0)在圆上
点A(x0,y0)在圆外
点A(x0,y0)在圆内
复习回顾
3.两条平行线Ax+By+C1=0与Ax+By+C2=0的距离是
2.平面内一点P(x0,y0) 到直线Ax+By+C=0的距离公式是
当A=0或B=0时,公式仍然成立.
1.两点间距离公式
复习回顾
“海上生明月,天涯共此时。” 表达了诗人望月怀人的深厚情谊。在海天交于一线的天际,一轮明月慢慢升起,先是探出半个圆圆的小脑袋,然后冉冉上升,和天际线相连,再跃出海面,越来越高,展现着迷人的风采.
这个过程中,月亮看作一个圆,海天交线看作一条直线,月出的过程中也体现了直线与圆的三种位置关系:相交、相切和相离.
情景导学
直线与圆的位置关系
直线与圆的位置关系:
(1)直线与圆相交,有两个公共点;
(2)直线与圆相切,只有一个公共点;
(3)直线与圆相离,没有公共点;
问题:如何用直线和圆的方程判断它们之间的位置关系?
学习新知
(1)利用圆心到直线的距离d与半径r的大小关系判断:
直线与圆的位置关系的判定方法:
直线l:Ax+By+C=0
圆C:(x-a)2+(y-b)2=r2(r>0)
d > r
d = r
d < r
直线与圆相离
直线与圆相切
直线与圆相交
学习新知
(2) 利用直线与圆的公共点n的个数进行判断:
n=0
n=1
n=2
相离
相切
相交
△<0
△=0
△>0
.
x
y
O
C
A
B
l
典型例题
代数法一
例1. 已知直线l:3x+y-6=0和圆心为C的圆x2+y2-2y-4=0,判断直线l与圆的位置关系;如果相交,求它们的交点坐标及弦长.
.
x
y
O
C
A
B
l
典型例题
代数法二
设而不求
例1. 已知直线l:3x+y-6=0和圆心为C的圆x2+y2-2y-4=0,判断直线l与圆的位置关系;如果相交,求它们的交点坐标及弦长.
例1. 已知直线l:3x+y-6=0和圆心为C的圆x2+y2-2y-4=0,判断直线l与圆的位置关系;如果相交,求它们的交点坐标及弦长.
.
x
y
O
C
A
B
l
典型例题
几何法
求直线与圆相交时弦长的两种方法
归纳总结
d
x
O
C
y
1.判断直线3x+4y+2=0与圆C:x2+y2-2x=0的位置关系.
巩固练习
几何法
P93 练习1
例2.过点P(2,1)作圆O:x2+y2=1的切线l,求切线l的方程.
典型例题
分析:如图,容易知道,点P(2,1)位于圆O:x2+y2=1外,经过圆外一点有两条直线与这个圆相切,我们设切线方程为y-1=k(x-2),k为斜率,由直线与圆相切可求出k的值.
因此,所求切线l的方程为y=1,或4x-3y-5=0.
例2.过点P(2,1)作圆O:x2+y2=1的切线l,求切线的方程.
典型例题
巩固练习
切线方程的求法
归纳总结
提醒:切线的斜率不存在的情况,不要漏解.
变式探究 过点Q(3,0)作圆x2+y2=4的切线,求此切线方程.
典型例题
.
x
y
O
M
.
E
F
1:已知直线l:kx-y+6=0被圆x2+y2=25截得的弦长为8,求k值.
巩固练习
2.求过点M(3,2)且和圆x2+y2=9相切的直线方程.
3.求圆心在直线2x+y=0上,过点P(2,1),且与直线x-y-1=0相切的圆方程.
小结:判断直线和圆的位置关系
几何方法
求圆心坐标及半径r(配方法)
圆心到直线的距离d (点到直线距离公式)
代数方法
消去y(或x)
作业
课本第98页
习题2.4第1,2,3,4题
Thank you for watching !
第二章 直线和圆的方程
2.5 直线与圆、圆与圆的位置关系
2.5.1 直线与圆的位置关系
一艘轮船在沿直线返回港口的途中,接到气象台的台风预报:台风中心位于轮船正西70km处,受影响的范围是半径长为30km的圆形区域。已知港口位于台风中心正北40km处,如果这艘轮船不改变航线,那么它是否会受到台风的影响?
.
x
O
y
港口
B
C
A
D
新课引入
复习回顾
名称
方程的形式
已知条件
方程直线的局限性
一般式
点斜式
斜截式
两点式
截距式
(x1,y1)是直线上一点,k是斜率
k是斜率,b是直线在y轴上的截距
不包括与x轴垂直的直线
a是直线在x轴上的截距,b是直线在y轴上的截距
(x1,y1),(x2,y2)是直线上两点
不包括与x轴垂直的直线
不包括与坐标轴垂直的直线
A、B、C为常数
任何位置的直线
不包括与坐标轴垂直的直线,不包括过原点的直线
Ax+By+C=0
(A、B不同时为零)
直线方程的五种形式
名称 标准方程 一般方程
方程形式
圆心
半径
点A(x0,y0)在圆上
点A(x0,y0)在圆外
点A(x0,y0)在圆内
复习回顾
3.两条平行线Ax+By+C1=0与Ax+By+C2=0的距离是
2.平面内一点P(x0,y0) 到直线Ax+By+C=0的距离公式是
当A=0或B=0时,公式仍然成立.
1.两点间距离公式
复习回顾
“海上生明月,天涯共此时。” 表达了诗人望月怀人的深厚情谊。在海天交于一线的天际,一轮明月慢慢升起,先是探出半个圆圆的小脑袋,然后冉冉上升,和天际线相连,再跃出海面,越来越高,展现着迷人的风采.
这个过程中,月亮看作一个圆,海天交线看作一条直线,月出的过程中也体现了直线与圆的三种位置关系:相交、相切和相离.
情景导学
直线与圆的位置关系
直线与圆的位置关系:
(1)直线与圆相交,有两个公共点;
(2)直线与圆相切,只有一个公共点;
(3)直线与圆相离,没有公共点;
问题:如何用直线和圆的方程判断它们之间的位置关系?
学习新知
(1)利用圆心到直线的距离d与半径r的大小关系判断:
直线与圆的位置关系的判定方法:
直线l:Ax+By+C=0
圆C:(x-a)2+(y-b)2=r2(r>0)
d > r
d = r
d < r
直线与圆相离
直线与圆相切
直线与圆相交
学习新知
(2) 利用直线与圆的公共点n的个数进行判断:
n=0
n=1
n=2
相离
相切
相交
△<0
△=0
△>0
.
x
y
O
C
A
B
l
典型例题
代数法一
例1. 已知直线l:3x+y-6=0和圆心为C的圆x2+y2-2y-4=0,判断直线l与圆的位置关系;如果相交,求它们的交点坐标及弦长.
.
x
y
O
C
A
B
l
典型例题
代数法二
设而不求
例1. 已知直线l:3x+y-6=0和圆心为C的圆x2+y2-2y-4=0,判断直线l与圆的位置关系;如果相交,求它们的交点坐标及弦长.
例1. 已知直线l:3x+y-6=0和圆心为C的圆x2+y2-2y-4=0,判断直线l与圆的位置关系;如果相交,求它们的交点坐标及弦长.
.
x
y
O
C
A
B
l
典型例题
几何法
求直线与圆相交时弦长的两种方法
归纳总结
d
x
O
C
y
1.判断直线3x+4y+2=0与圆C:x2+y2-2x=0的位置关系.
巩固练习
几何法
P93 练习1
例2.过点P(2,1)作圆O:x2+y2=1的切线l,求切线l的方程.
典型例题
分析:如图,容易知道,点P(2,1)位于圆O:x2+y2=1外,经过圆外一点有两条直线与这个圆相切,我们设切线方程为y-1=k(x-2),k为斜率,由直线与圆相切可求出k的值.
因此,所求切线l的方程为y=1,或4x-3y-5=0.
例2.过点P(2,1)作圆O:x2+y2=1的切线l,求切线的方程.
典型例题
巩固练习
切线方程的求法
归纳总结
提醒:切线的斜率不存在的情况,不要漏解.
变式探究 过点Q(3,0)作圆x2+y2=4的切线,求此切线方程.
典型例题
.
x
y
O
M
.
E
F
1:已知直线l:kx-y+6=0被圆x2+y2=25截得的弦长为8,求k值.
巩固练习
2.求过点M(3,2)且和圆x2+y2=9相切的直线方程.
3.求圆心在直线2x+y=0上,过点P(2,1),且与直线x-y-1=0相切的圆方程.
小结:判断直线和圆的位置关系
几何方法
求圆心坐标及半径r(配方法)
圆心到直线的距离d (点到直线距离公式)
代数方法
消去y(或x)
作业
课本第98页
习题2.4第1,2,3,4题
Thank you for watching !
