高中数学人教B版(2019)必修第二册 5.1.4用样本估计总体课件(共24张PPT)
文档属性
| 名称 | 高中数学人教B版(2019)必修第二册 5.1.4用样本估计总体课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-29 21:22:17 | ||
图片预览







文档简介
(共24张PPT)
5.1.4用样本估计总体
问题1.用样本的数字特征估计总体的数字特征
问题2:分层抽样下用样本的数字特征估计总体的数字特征
依照上述公式可以算出,前述尝试与发现(2)中总体的平均数可以估计为167.86,总体的方差可以估计为25.98.
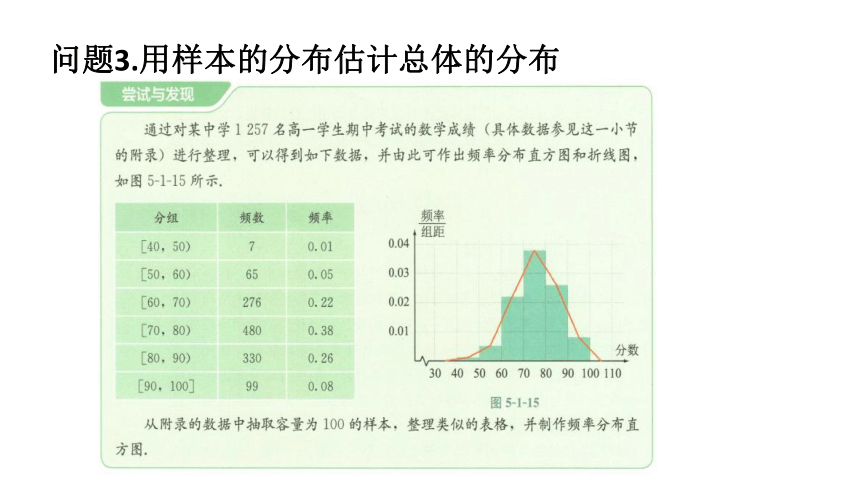
问题3.用样本的分布估计总体的分布
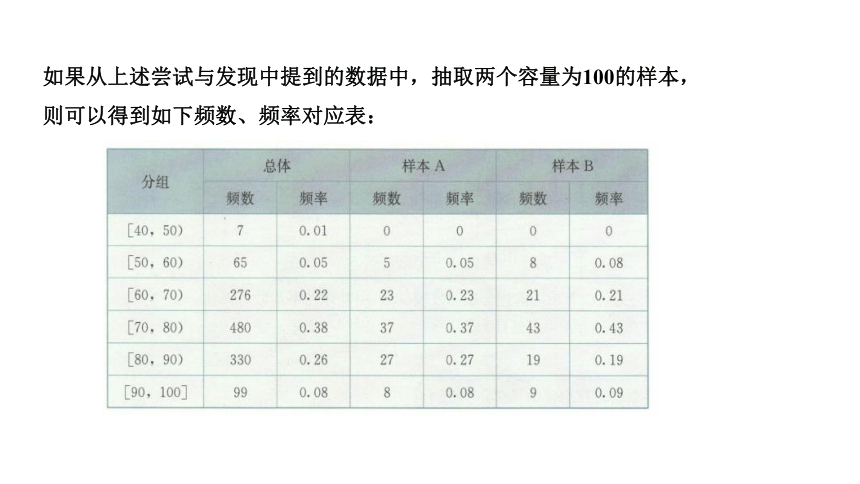
如果从上述尝试与发现中提到的数据中,抽取两个容量为100的样本,则可以得到如下频数、频率对应表:
例1.为了快速了解某学校学生体重(单位:Kg)的大致情况,随机抽取了10名学生称重,得到的数据整理成茎叶图如图所示,估计这个学校学生体重的平均数和方差.
【解题方法】
1.众数、中位数、平均数与频率分布表、频率分布直方图的关系
(1)众数:众数一般用频率分布表中频率最高的一小组的组中值来表示,即在样本数据的频率分布直方图中,最高矩形的底边中点的横坐标.
(2)中位数:在频率分布表中,中位数是累计频率(样本数据小于某一数值的频率叫作该数值点的累计频率)为0.5时所对应的样本数据的值,而在样本中有50%的个体小于或等于中位数,也有50%的个体大于或等于中位数.因此,在频率分布直方图中,中位数左边和右边的直方图的面积应该相等.
(3)平均数:平均数在频率分布直方图中等于每个小矩形底边中点的横坐标与小矩形的面积的乘积之和.又平均数是频率分布直方图的“重心”.
2.利用直方图求众数、中位数、平均数均为近似值,往往与实际数据得出的不一致,但它们能粗略估计其众数、中位数和平均数.
小结:
1. 样本平均数与总体平均数的关系:
①在简单随机抽样中,我们常用样本平均数去估计总体平均数.
②一般地,大部分样本平均数离总体平均数不远,在总体平均数附近波动.样本量越大,波动幅度越小.
2. 计算样本平均数、样本方差直接利用公式,在按比例分配分层随机抽样中,我们可以用样本平均数和样本方差估计总体平均数和总体方差.
3. 众数、中位数分别是频率分布直方图中最高的小矩形的中间值、累计频率为0.5时所对应的样本数据的值,平均数为每个小矩形底边中点的横坐标与小矩形的面积的乘积之和.
5.1.4用样本估计总体
问题1.用样本的数字特征估计总体的数字特征
问题2:分层抽样下用样本的数字特征估计总体的数字特征
依照上述公式可以算出,前述尝试与发现(2)中总体的平均数可以估计为167.86,总体的方差可以估计为25.98.
问题3.用样本的分布估计总体的分布
如果从上述尝试与发现中提到的数据中,抽取两个容量为100的样本,则可以得到如下频数、频率对应表:
例1.为了快速了解某学校学生体重(单位:Kg)的大致情况,随机抽取了10名学生称重,得到的数据整理成茎叶图如图所示,估计这个学校学生体重的平均数和方差.
【解题方法】
1.众数、中位数、平均数与频率分布表、频率分布直方图的关系
(1)众数:众数一般用频率分布表中频率最高的一小组的组中值来表示,即在样本数据的频率分布直方图中,最高矩形的底边中点的横坐标.
(2)中位数:在频率分布表中,中位数是累计频率(样本数据小于某一数值的频率叫作该数值点的累计频率)为0.5时所对应的样本数据的值,而在样本中有50%的个体小于或等于中位数,也有50%的个体大于或等于中位数.因此,在频率分布直方图中,中位数左边和右边的直方图的面积应该相等.
(3)平均数:平均数在频率分布直方图中等于每个小矩形底边中点的横坐标与小矩形的面积的乘积之和.又平均数是频率分布直方图的“重心”.
2.利用直方图求众数、中位数、平均数均为近似值,往往与实际数据得出的不一致,但它们能粗略估计其众数、中位数和平均数.
小结:
1. 样本平均数与总体平均数的关系:
①在简单随机抽样中,我们常用样本平均数去估计总体平均数.
②一般地,大部分样本平均数离总体平均数不远,在总体平均数附近波动.样本量越大,波动幅度越小.
2. 计算样本平均数、样本方差直接利用公式,在按比例分配分层随机抽样中,我们可以用样本平均数和样本方差估计总体平均数和总体方差.
3. 众数、中位数分别是频率分布直方图中最高的小矩形的中间值、累计频率为0.5时所对应的样本数据的值,平均数为每个小矩形底边中点的横坐标与小矩形的面积的乘积之和.
