2020-2021学年人教版八年级下册数学第18章《平行四边形》(3)(含答案)
文档属性
| 名称 | 2020-2021学年人教版八年级下册数学第18章《平行四边形》(3)(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 430.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-29 13:25:33 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
《平行四边形》单元测试
题号 一 二 三 总分
19 20 21 22 23 24
分数
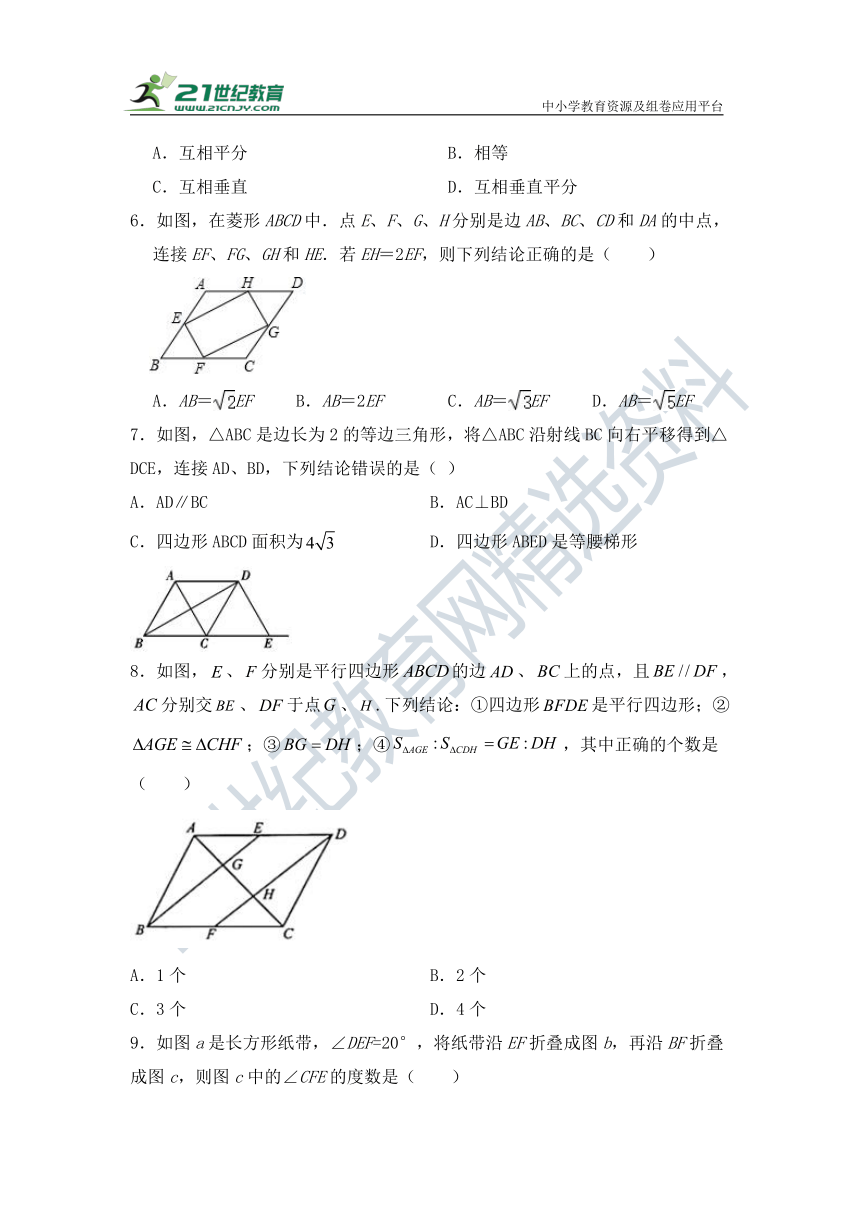
一.选择题(每题3分,共30分)
1.在四边形中,给出下列条件:①;②;③;④.从以上选择两个条件使四边形为平行四边形的选法有( )
A.3种 B.4种 C.5种 D.6种
2.下列命题中,是真命题的为( )
A.一组对边平行,另一组对边相等的四边形是平行四边形.
B.对角线互相垂直的四边形是菱形
C.一组邻边相等的矩形是正方形
D.对角线相等且互相垂直的四边形是矩形
3.如图,四边形ABCD的对角线交于点O,下列不能判定四边形ABCD为平行四边形的是( )
A.AB=CD,AD=BC B.∠ABC=∠ADC,AB∥CD
C.OA=OC,OB=OD D.AB∥CD,AD=BC
4. 如图所示,已知等边三角形ABC的边长为,按图中所示的规律,用个这样的三角形镶嵌而成的四边形的周长是( )
A. B. C. D.
5.如果顺次连接四边形的各边中点得到的四边形是矩形,那么原来四边形的对角线一定满足的条件是( )
A.互相平分 B.相等
C.互相垂直 D.互相垂直平分
6.如图,在菱形ABCD中.点E、F、G、H分别是边AB、BC、CD和DA的中点,连接EF、FG、GH和HE.若EH=2EF,则下列结论正确的是( )
A.AB=EF B.AB=2EF C.AB=EF D.AB=EF
7.如图,△ABC是边长为2的等边三角形,将△ABC沿射线BC向右平移得到△DCE,连接AD、BD,下列结论错误的是( )
A.AD∥BC B.AC⊥BD
C.四边形ABCD面积为 D.四边形ABED是等腰梯形
8.如图,、分别是平行四边形的边、上的点,且,分别交、于点、.下列结论:①四边形是平行四边形;②;③;④,其中正确的个数是( )
A.1个 B.2个
C.3个 D.4个
9.如图a是长方形纸带,∠DEF=20°,将纸带沿EF折叠成图b,再沿BF折叠成图c,则图c中的∠CFE的度数是( )
A.110° B.120° C.140° D.150°
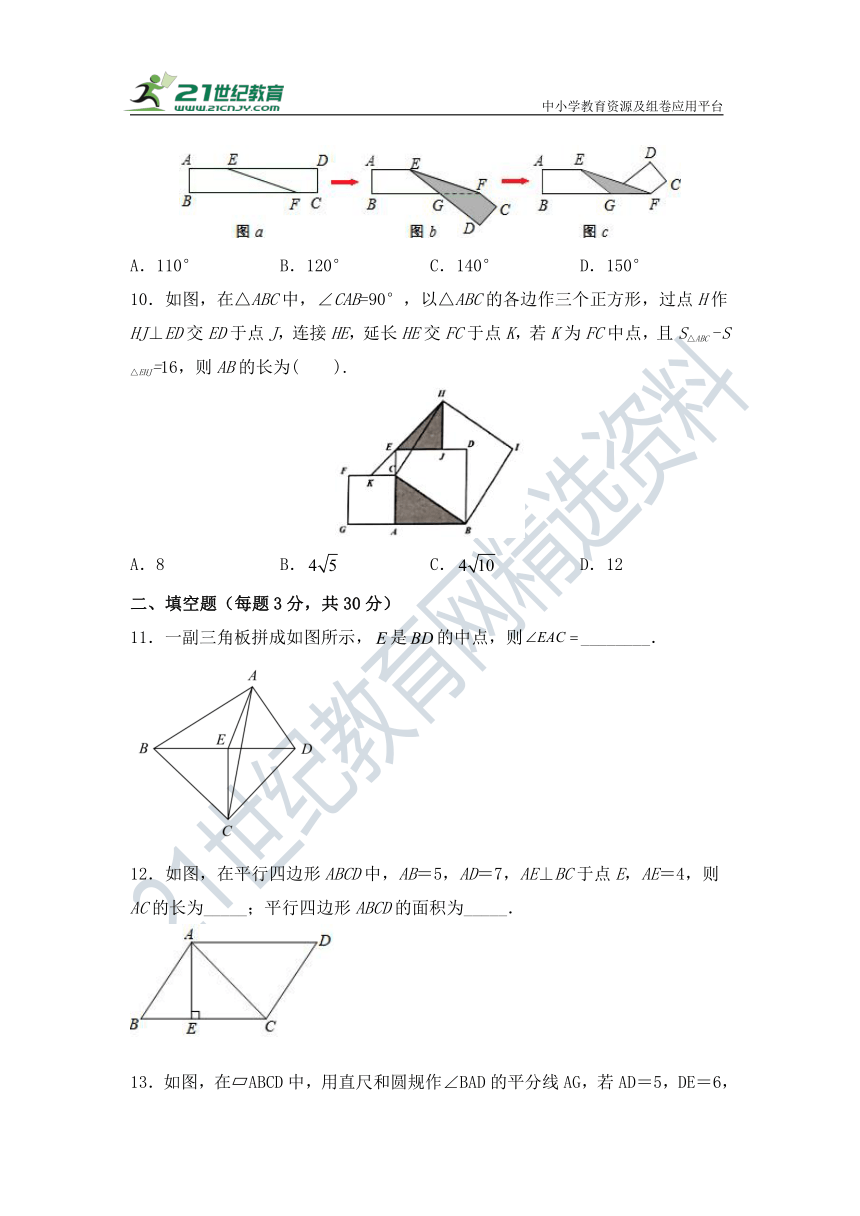
10.如图,在△ABC中,∠CAB=90°,以△ABC的各边作三个正方形,过点H作HJ⊥ED交ED于点J,连接HE,延长HE交FC于点K,若K为FC中点,且S△ABC -S△EHJ=16,则AB的长为( ).
A.8 B. C. D.12
二、填空题(每题3分,共30分)
11.一副三角板拼成如图所示,是的中点,则________.
12.如图,在平行四边形ABCD中,AB=5,AD=7,AE⊥BC于点E,AE=4,则AC的长为_____;平行四边形ABCD的面积为_____.
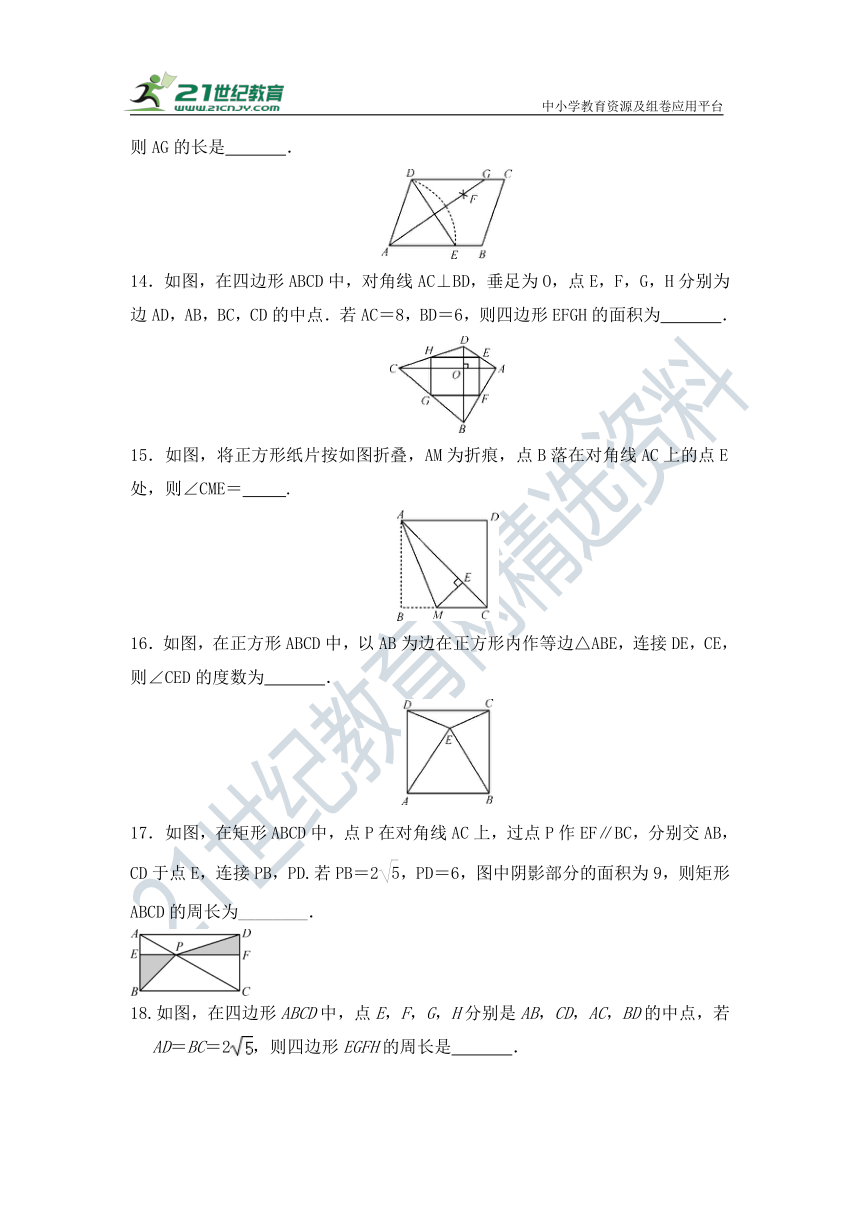
13.如图,在 ABCD中,用直尺和圆规作∠BAD的平分线AG,若AD=5,DE=6,则AG的长是 .
14.如图,在四边形ABCD中,对角线AC⊥BD,垂足为O,点E,F,G,H分别为边AD,AB,BC,CD的中点.若AC=8,BD=6,则四边形EFGH的面积为 .
15.如图,将正方形纸片按如图折叠,AM为折痕,点B落在对角线AC上的点E处,则∠CME= .
16.如图,在正方形ABCD中,以AB为边在正方形内作等边△ABE,连接DE,CE,则∠CED的度数为 .
如图,在矩形ABCD中,点P在对角线AC上,过点P作EF∥BC,分别交AB,CD于点E,连接PB,PD.若PB=2,PD=6,图中阴影部分的面积为9,则矩形ABCD的周长为________.
18.如图,在四边形ABCD中,点E,F,G,H分别是AB,CD,AC,BD的中点,若AD=BC=2,则四边形EGFH的周长是 .
三、解答题(本题共有6小题,共46分)
19.(6分)如图,B,E,C,F在一条直线上,已知AB∥DE,AC∥DF,BE=CF,连接AD.求证:四边形ABED是平行四边形.
20.(8分)如图,在菱形ABCD中,对角线AC、BD相交于点O,过点D作对角线BD的垂线交BA的延长线于点E.
(1)证明:四边形ACDE是平行四边形;
(2)若AC=8,BD=6,求△ADE的周长.
22、(8分)如图,AC是矩形ABCD的对角线,过AC的中点O作EF⊥AC,交BC于点E,交AD于点F,连接AE,CF.
(1)求证:四边形AECF是菱形;
(2)若AB=,∠DCF=30°,求四边形AECF的面积.(结果保留根号)
23.(8分)如图,把长方形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C′的位置上.
(1)若∠1=55°,求∠2、∠3的度数;
(2)若AB=12,AD=18,求△BC′F的面积.
24.(8分)如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD,BE.
(1)求证:CE=AD;
(2)当D为AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.
参考答案
选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 B C A C B D C D B D
二.填空题
11.15°
解:由题意可得:∠BAD=∠BCD=90°,∠ABD=30°,∠CBD=45°,
∵E是BD中点,
∴AE=BE=BD,CE=BE=BD,
∴AE=CE,
∵AE=BE,
∴∠EAB=∠ABD=30°,
∴∠AED=∠EAB+∠ABD=60°,
∵EB=EC,
∴∠ECB=∠EBC=45°,
∴∠CED=∠ECB+∠EBC=90°,
∴∠AEC=∠CED+∠AED=150°,
∵AE=CE,
∴∠EAC==15°,
12. 28
13.如图,在 ABCD中,用直尺和圆规作∠BAD的平分线AG,若AD=5,DE=6,则AG的长是8.
14.如图,在四边形ABCD中,对角线AC⊥BD,垂足为O,点E,F,G,H分别为边AD,AB,BC,CD的中点.若AC=8,BD=6,则四边形EFGH的面积为12.
15.如图,将正方形纸片按如图折叠,AM为折痕,点B落在对角线AC上的点E处,则∠CME=45°.
16.如图,在正方形ABCD中,以AB为边在正方形内作等边△ABE,连接DE,CE,则∠CED的度数为150°.
.2+6
18.4.
三、解答题
19.证明:∵AB∥DE,AC∥DF,∴∠B=∠DEF,∠ACB=∠F.BE=CF,∴BE+CE=CF+CE,∴BC=EF.在△ABC和△DEF中,∴△ABC≌△DEF(ASA).∴AB=DE.又∵AB∥DE,∴四边形ABED是平行四边形.
20.(1)证明:∵四边形ABCD是菱形,∴AB∥CD,AC⊥BD,∴AE∥CD,∠AOB=90°,∵DE⊥BD,即∠EDB=90°,∴∠AOB=∠EDB,∴DE∥AC,∴四边形ACDE是平行四边形. (2)∵四边形ABCD是菱形,AC=8,BD=6,∴AO=4,DO=3,AD=CD=5,∵四边形ACDE是平行四边形,∴AE=CD=5,DE=AC=8,∴△ADE的周长为AD+AE+DE=5+5+8=18.
21、解:四边形ABCD是平行四边形.
理由:∵A(﹣3,﹣2),B(0,3),C(3,2),D(0,﹣3),
∴AB=CD,BC=AD,
∴四边形ABCD是平行四边形.
22、(1)证明:∵O是AC的中点,且EF⊥AC,
∴AF=CF,AE=CE,OA=OC,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠AFO=∠CEO,
在△AOF和△COE中,
,
∴△AOF≌△COE(AAS),
∴AF=CE,
∴AF=CF=CE=AE,
∴四边形AECF是菱形;
(2)解:∵四边形ABCD是矩形,
∴CD=AB=,
在Rt△CDF中,cos∠DCF=,∠DCF=30°,
∴CF==2,
∵四边形AECF是菱形,
∴CE=CF=2,
∴四边形AECF是的面积为:EC AB=2.
23.(1)∠2=55°,∠3=70°;(2)
24.如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD,BE.
(1)求证:CE=AD;
(2)当D为AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.
解:(1)证明:∵DE⊥BC,
∴∠DFB=90°.
又∵∠ACB=90°,
∴∠ACB=∠DFB.
∴AC∥DE.
又∵MN∥AB,即CE∥AD,
∴四边形ADEC是平行四边形.
∴CE=AD.
(2)四边形BECD是菱形.理由:
∵D为AB中点,∴AD=BD.
又由(1)得CE=AD,∴BD=CE.
又∵BD∥CE,∴四边形BECD是平行四边形.
又∵DE⊥BC,
∴四边形BECD是菱形.
(3)当∠A=45°时,四边形BECD是正方形.理由:
∵∠ACB=90°,∠A=45°,
∴∠ABC=∠A=45°.∴AC=BC.
又∵D为AB中点,∴CD⊥AB,即∠CDB=90°.
又∵四边形BECD是菱形,
∴四边形BECD是正方形.
∴当∠A=45°时,四边形BECD是正方形.
题
C
A
B
┅┅
《平行四边形》单元测试
题号 一 二 三 总分
19 20 21 22 23 24
分数
一.选择题(每题3分,共30分)
1.在四边形中,给出下列条件:①;②;③;④.从以上选择两个条件使四边形为平行四边形的选法有( )
A.3种 B.4种 C.5种 D.6种
2.下列命题中,是真命题的为( )
A.一组对边平行,另一组对边相等的四边形是平行四边形.
B.对角线互相垂直的四边形是菱形
C.一组邻边相等的矩形是正方形
D.对角线相等且互相垂直的四边形是矩形
3.如图,四边形ABCD的对角线交于点O,下列不能判定四边形ABCD为平行四边形的是( )
A.AB=CD,AD=BC B.∠ABC=∠ADC,AB∥CD
C.OA=OC,OB=OD D.AB∥CD,AD=BC
4. 如图所示,已知等边三角形ABC的边长为,按图中所示的规律,用个这样的三角形镶嵌而成的四边形的周长是( )
A. B. C. D.
5.如果顺次连接四边形的各边中点得到的四边形是矩形,那么原来四边形的对角线一定满足的条件是( )
A.互相平分 B.相等
C.互相垂直 D.互相垂直平分
6.如图,在菱形ABCD中.点E、F、G、H分别是边AB、BC、CD和DA的中点,连接EF、FG、GH和HE.若EH=2EF,则下列结论正确的是( )
A.AB=EF B.AB=2EF C.AB=EF D.AB=EF
7.如图,△ABC是边长为2的等边三角形,将△ABC沿射线BC向右平移得到△DCE,连接AD、BD,下列结论错误的是( )
A.AD∥BC B.AC⊥BD
C.四边形ABCD面积为 D.四边形ABED是等腰梯形
8.如图,、分别是平行四边形的边、上的点,且,分别交、于点、.下列结论:①四边形是平行四边形;②;③;④,其中正确的个数是( )
A.1个 B.2个
C.3个 D.4个
9.如图a是长方形纸带,∠DEF=20°,将纸带沿EF折叠成图b,再沿BF折叠成图c,则图c中的∠CFE的度数是( )
A.110° B.120° C.140° D.150°
10.如图,在△ABC中,∠CAB=90°,以△ABC的各边作三个正方形,过点H作HJ⊥ED交ED于点J,连接HE,延长HE交FC于点K,若K为FC中点,且S△ABC -S△EHJ=16,则AB的长为( ).
A.8 B. C. D.12
二、填空题(每题3分,共30分)
11.一副三角板拼成如图所示,是的中点,则________.
12.如图,在平行四边形ABCD中,AB=5,AD=7,AE⊥BC于点E,AE=4,则AC的长为_____;平行四边形ABCD的面积为_____.
13.如图,在 ABCD中,用直尺和圆规作∠BAD的平分线AG,若AD=5,DE=6,则AG的长是 .
14.如图,在四边形ABCD中,对角线AC⊥BD,垂足为O,点E,F,G,H分别为边AD,AB,BC,CD的中点.若AC=8,BD=6,则四边形EFGH的面积为 .
15.如图,将正方形纸片按如图折叠,AM为折痕,点B落在对角线AC上的点E处,则∠CME= .
16.如图,在正方形ABCD中,以AB为边在正方形内作等边△ABE,连接DE,CE,则∠CED的度数为 .
如图,在矩形ABCD中,点P在对角线AC上,过点P作EF∥BC,分别交AB,CD于点E,连接PB,PD.若PB=2,PD=6,图中阴影部分的面积为9,则矩形ABCD的周长为________.
18.如图,在四边形ABCD中,点E,F,G,H分别是AB,CD,AC,BD的中点,若AD=BC=2,则四边形EGFH的周长是 .
三、解答题(本题共有6小题,共46分)
19.(6分)如图,B,E,C,F在一条直线上,已知AB∥DE,AC∥DF,BE=CF,连接AD.求证:四边形ABED是平行四边形.
20.(8分)如图,在菱形ABCD中,对角线AC、BD相交于点O,过点D作对角线BD的垂线交BA的延长线于点E.
(1)证明:四边形ACDE是平行四边形;
(2)若AC=8,BD=6,求△ADE的周长.
22、(8分)如图,AC是矩形ABCD的对角线,过AC的中点O作EF⊥AC,交BC于点E,交AD于点F,连接AE,CF.
(1)求证:四边形AECF是菱形;
(2)若AB=,∠DCF=30°,求四边形AECF的面积.(结果保留根号)
23.(8分)如图,把长方形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C′的位置上.
(1)若∠1=55°,求∠2、∠3的度数;
(2)若AB=12,AD=18,求△BC′F的面积.
24.(8分)如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD,BE.
(1)求证:CE=AD;
(2)当D为AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.
参考答案
选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 B C A C B D C D B D
二.填空题
11.15°
解:由题意可得:∠BAD=∠BCD=90°,∠ABD=30°,∠CBD=45°,
∵E是BD中点,
∴AE=BE=BD,CE=BE=BD,
∴AE=CE,
∵AE=BE,
∴∠EAB=∠ABD=30°,
∴∠AED=∠EAB+∠ABD=60°,
∵EB=EC,
∴∠ECB=∠EBC=45°,
∴∠CED=∠ECB+∠EBC=90°,
∴∠AEC=∠CED+∠AED=150°,
∵AE=CE,
∴∠EAC==15°,
12. 28
13.如图,在 ABCD中,用直尺和圆规作∠BAD的平分线AG,若AD=5,DE=6,则AG的长是8.
14.如图,在四边形ABCD中,对角线AC⊥BD,垂足为O,点E,F,G,H分别为边AD,AB,BC,CD的中点.若AC=8,BD=6,则四边形EFGH的面积为12.
15.如图,将正方形纸片按如图折叠,AM为折痕,点B落在对角线AC上的点E处,则∠CME=45°.
16.如图,在正方形ABCD中,以AB为边在正方形内作等边△ABE,连接DE,CE,则∠CED的度数为150°.
.2+6
18.4.
三、解答题
19.证明:∵AB∥DE,AC∥DF,∴∠B=∠DEF,∠ACB=∠F.BE=CF,∴BE+CE=CF+CE,∴BC=EF.在△ABC和△DEF中,∴△ABC≌△DEF(ASA).∴AB=DE.又∵AB∥DE,∴四边形ABED是平行四边形.
20.(1)证明:∵四边形ABCD是菱形,∴AB∥CD,AC⊥BD,∴AE∥CD,∠AOB=90°,∵DE⊥BD,即∠EDB=90°,∴∠AOB=∠EDB,∴DE∥AC,∴四边形ACDE是平行四边形. (2)∵四边形ABCD是菱形,AC=8,BD=6,∴AO=4,DO=3,AD=CD=5,∵四边形ACDE是平行四边形,∴AE=CD=5,DE=AC=8,∴△ADE的周长为AD+AE+DE=5+5+8=18.
21、解:四边形ABCD是平行四边形.
理由:∵A(﹣3,﹣2),B(0,3),C(3,2),D(0,﹣3),
∴AB=CD,BC=AD,
∴四边形ABCD是平行四边形.
22、(1)证明:∵O是AC的中点,且EF⊥AC,
∴AF=CF,AE=CE,OA=OC,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠AFO=∠CEO,
在△AOF和△COE中,
,
∴△AOF≌△COE(AAS),
∴AF=CE,
∴AF=CF=CE=AE,
∴四边形AECF是菱形;
(2)解:∵四边形ABCD是矩形,
∴CD=AB=,
在Rt△CDF中,cos∠DCF=,∠DCF=30°,
∴CF==2,
∵四边形AECF是菱形,
∴CE=CF=2,
∴四边形AECF是的面积为:EC AB=2.
23.(1)∠2=55°,∠3=70°;(2)
24.如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD,BE.
(1)求证:CE=AD;
(2)当D为AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.
解:(1)证明:∵DE⊥BC,
∴∠DFB=90°.
又∵∠ACB=90°,
∴∠ACB=∠DFB.
∴AC∥DE.
又∵MN∥AB,即CE∥AD,
∴四边形ADEC是平行四边形.
∴CE=AD.
(2)四边形BECD是菱形.理由:
∵D为AB中点,∴AD=BD.
又由(1)得CE=AD,∴BD=CE.
又∵BD∥CE,∴四边形BECD是平行四边形.
又∵DE⊥BC,
∴四边形BECD是菱形.
(3)当∠A=45°时,四边形BECD是正方形.理由:
∵∠ACB=90°,∠A=45°,
∴∠ABC=∠A=45°.∴AC=BC.
又∵D为AB中点,∴CD⊥AB,即∠CDB=90°.
又∵四边形BECD是菱形,
∴四边形BECD是正方形.
∴当∠A=45°时,四边形BECD是正方形.
题
C
A
B
┅┅
