平行线的判定
图片预览





文档简介
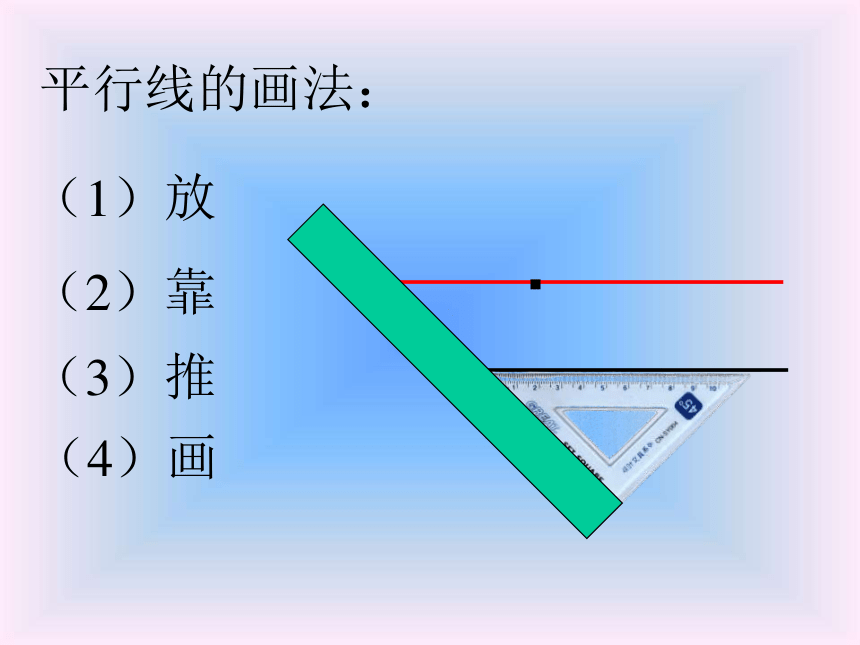
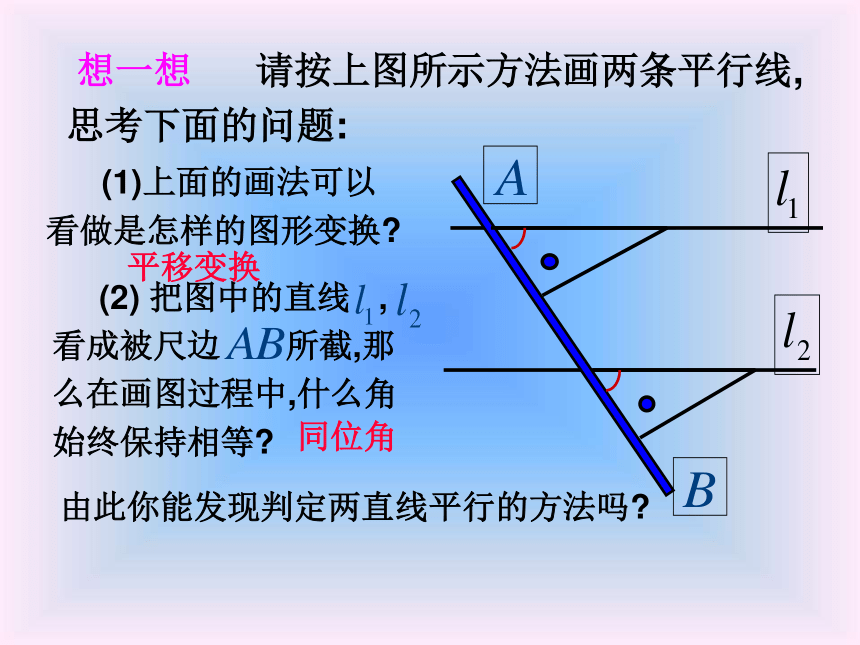
课件22张PPT。平行线的判定判定两条直线平行的方法有两种:定义: 在同一平面内,不相交的两条直线叫平行线。平行公理的推论:除应用以上两种方法以外,是否还有其它方法呢?如果两条直线平行于同一条直线,那么这两条直线平行。平行线的画法:(1)放(2)靠(3)推(4)画· 想一想 请按上图所示方法画两条平行线,思考下面的问题: (1)上面的画法可以看做是怎样的图形变换?平移变换同位角由此你能发现判定两直线平行的方法吗? 平行线的判定方法1
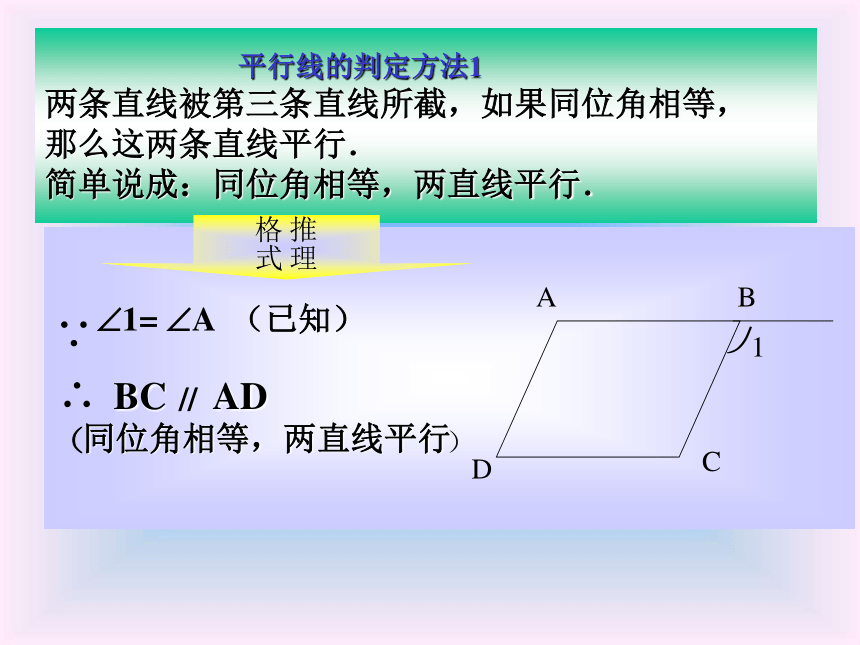
两条直线被第三条直线所截,如果同位角相等,
那么这两条直线平行.
简单说成:同位角相等,两直线平行.BC AD同位角相等,两直线平行推理
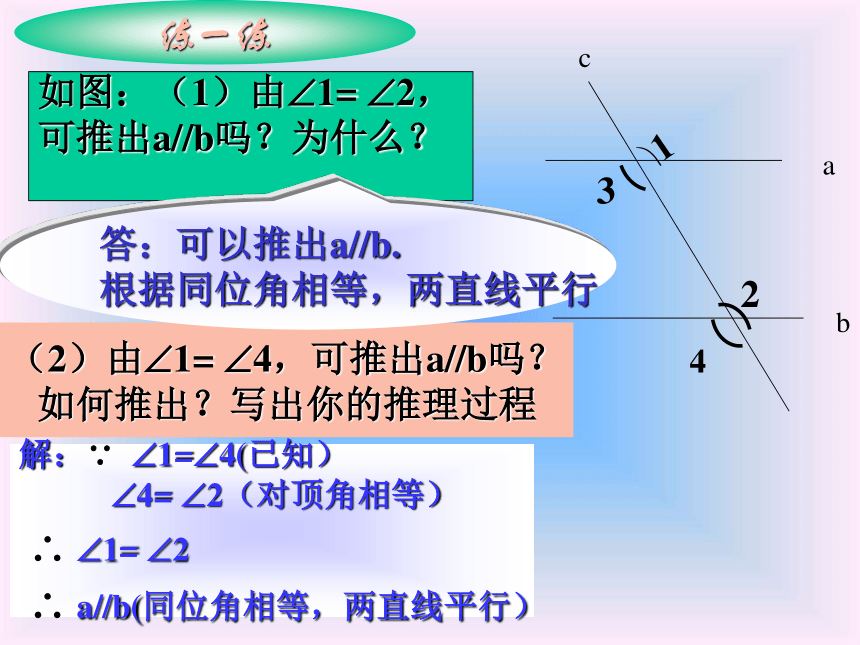
格式3如图:(1)由?1= ?2,
可推出a//b吗?为什么?
(2)由?1= ?4,可推出a//b吗?
如何推出?写出你的推理过程练一练答:可以推出a//b.
根据同位角相等,两直线平行解:∵ ?1=?4(已知)
?4= ?2(对顶角相等)
? ?1= ?2
? a//b(同位角相等,两直线平行)4如图,直线AB,CD被直线EF所截。
若∠ 2= ∠ 3,则AB与CD平行吗?解: ∵ ∠ 2= ∠ 3 (已知)
∠ 1= ∠ 3 (对顶角相等)∴ ∠1= ∠ 2 ∴ AB//CD(同位角相等,两直线平行)
合作学习,分组讨论ABCDEF由此你又获得怎样的
判定两直线平行的方法吗?
平行线判定方法2:
两条直线被第三条直线所截,如果内错角相等 ,那么这两条直线平行。简单的说:内错角相等,两直线平行。练习:
1.如图,
1) ∵∠1=∠2,
∴ ∥ .
( )
2) ∵ = ,(或 = )
∴ AB∥DC
( )
(或 )ABCD12EADBC内错角相等,两直线平行∠B∠DCE∠BAC∠ACD同位角相等,两直线平行内错角相等,两直线平行2.如图已知∠1=120°,
∠2=120°, ∠3=120°,
说出其中的平行线,并说明理由。L2L1
L4
L3
123想一想:如图,直线a、b被直线c所截,
若∠2+∠3=180°,
则a b abc1234∥
平行线判定方法3:
两条直线被第三条直线所截,如果同旁内角互补 ,那么这两条直线平行。简单的说:同旁内角互补,两直线平行。 练习:
3.如图,已知∠A与∠D互补,
可以判定哪两条直线平行?
∠B与哪个角互补,可以判
定直线AD∥BC? ABCD 解:
1) ∵ ∠A与∠D互补(已知)
∴AB∥DC(同旁内角互补,两直线平行)
2) ∠B与∠A互补时
可判定AD∥BC(同旁内角互补,两直线平行) 4 . 在同一平面内,两条直线垂直
于同一条直线,这两条直线平行吗?
为什么?答:在同一平面内,垂直于同一条直线
的两条直线平行。
方法 1
如图
∵ b⊥a,c⊥a(已知)
∴∠1=∠2=90°(垂直定义)
∴b∥c(同位角相等,两直线平行) 方法 2
如图
∵ b⊥a,c⊥a(已知)
∴∠1=∠2=90°(垂直定义)
∴b∥c(内错角相等,两直线平行)1方法 3
如图
∵ b⊥a,c⊥a(已知)
∴∠1=∠2=90°(垂直定义)
∴ ∠1+∠2=180°
∴b∥c(同旁内角互补,两直线平行)12这节课我们学了什么?平行线判定方法1:同位角相等,两直线平行。
平行线判定方法2:内错角相等,两直线平行。
平行线判定方法3:同旁内角互补,两直线平行。你记住了吗?布置作业
作业1(必做):P16。1,2
作业2(选做):P17。7 谢谢!
两条直线被第三条直线所截,如果同位角相等,
那么这两条直线平行.
简单说成:同位角相等,两直线平行.BC AD同位角相等,两直线平行推理
格式3如图:(1)由?1= ?2,
可推出a//b吗?为什么?
(2)由?1= ?4,可推出a//b吗?
如何推出?写出你的推理过程练一练答:可以推出a//b.
根据同位角相等,两直线平行解:∵ ?1=?4(已知)
?4= ?2(对顶角相等)
? ?1= ?2
? a//b(同位角相等,两直线平行)4如图,直线AB,CD被直线EF所截。
若∠ 2= ∠ 3,则AB与CD平行吗?解: ∵ ∠ 2= ∠ 3 (已知)
∠ 1= ∠ 3 (对顶角相等)∴ ∠1= ∠ 2 ∴ AB//CD(同位角相等,两直线平行)
合作学习,分组讨论ABCDEF由此你又获得怎样的
判定两直线平行的方法吗?
平行线判定方法2:
两条直线被第三条直线所截,如果内错角相等 ,那么这两条直线平行。简单的说:内错角相等,两直线平行。练习:
1.如图,
1) ∵∠1=∠2,
∴ ∥ .
( )
2) ∵ = ,(或 = )
∴ AB∥DC
( )
(或 )ABCD12EADBC内错角相等,两直线平行∠B∠DCE∠BAC∠ACD同位角相等,两直线平行内错角相等,两直线平行2.如图已知∠1=120°,
∠2=120°, ∠3=120°,
说出其中的平行线,并说明理由。L2L1
L4
L3
123想一想:如图,直线a、b被直线c所截,
若∠2+∠3=180°,
则a b abc1234∥
平行线判定方法3:
两条直线被第三条直线所截,如果同旁内角互补 ,那么这两条直线平行。简单的说:同旁内角互补,两直线平行。 练习:
3.如图,已知∠A与∠D互补,
可以判定哪两条直线平行?
∠B与哪个角互补,可以判
定直线AD∥BC? ABCD 解:
1) ∵ ∠A与∠D互补(已知)
∴AB∥DC(同旁内角互补,两直线平行)
2) ∠B与∠A互补时
可判定AD∥BC(同旁内角互补,两直线平行) 4 . 在同一平面内,两条直线垂直
于同一条直线,这两条直线平行吗?
为什么?答:在同一平面内,垂直于同一条直线
的两条直线平行。
方法 1
如图
∵ b⊥a,c⊥a(已知)
∴∠1=∠2=90°(垂直定义)
∴b∥c(同位角相等,两直线平行) 方法 2
如图
∵ b⊥a,c⊥a(已知)
∴∠1=∠2=90°(垂直定义)
∴b∥c(内错角相等,两直线平行)1方法 3
如图
∵ b⊥a,c⊥a(已知)
∴∠1=∠2=90°(垂直定义)
∴ ∠1+∠2=180°
∴b∥c(同旁内角互补,两直线平行)12这节课我们学了什么?平行线判定方法1:同位角相等,两直线平行。
平行线判定方法2:内错角相等,两直线平行。
平行线判定方法3:同旁内角互补,两直线平行。你记住了吗?布置作业
作业1(必做):P16。1,2
作业2(选做):P17。7 谢谢!
