2020-2021学年人教版八年级下册数学第18章《平行四边形》(3)(含答案)
文档属性
| 名称 | 2020-2021学年人教版八年级下册数学第18章《平行四边形》(3)(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 424.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-29 17:19:06 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
《平行四边形》单元测试
题号 一 二 三 总分
19 20 21 22 23 24
分数
一.选择题(每题3分,共30分)
1.下列说法中,错误的是
A.平行四边形的对角线互相平分 B.对角线互相平分的四边形是平行四边
C.菱形的对角线互相垂直 D.对角线互相垂直的四边形是菱形
2.如图所示,在中,,是上的点,交于点,交于点,那么四边形的周长是
A.5 B.10 C.15 D.20
3.如图所示,在中,对角线,交于点,图中全等三角形有
A.5对 B.4对 C.3对 D.2对
4.在平行四边形ABCD中,对角线AC、BD相交于点O,以点O为坐标原点建立平面直角坐标系,其中A(a,b),B(a-1,b+2),C(3,1),则点D的坐标是( )
A.(4,-1) B.(-3,-1) C.(2,3) D.(-4,1)
5.如图,在菱形ABCD中,AC与BD相交于点O,AC=6,BD=8,则菱形边长AB等于( )
A.10 B. C.5 D.6
5题图 6题图 7题图
6.小玲的爸爸在钉制平行四边形框架时,采用了一种方法:如图,将两根木条AC、BD的中点重叠并用钉子固定,则四边形ABCD就是平行四边形,这种方法的依据是( )
A.对角线互相平分的四边形是平行四边形
B.两组对角分别相等的四边形是平行四边形
C.两组对边分别相等的四边形是平行四边形
D.两组对边分别平行的四边形是平行四边形
7.如图,矩形ABCD的两条对角线相交于点O,∠AOD=60°,AD=4,则该矩形的面积是( )
A.16 B.8 C.16 D.8
8.如图所示,在矩形ABCD中,AB=4,AD=3,矩形内部有一动点P满足S△PAB=S矩形ABCD,则点P到A,B两点的距离之和PA+PB的最小值为( )
A.5 B.2 C.2 D.4
9.如图,在正方形ABCD中,AB=3,点E,F分别在CD,AD上,CE=DF,BE,CF相交于点G.若图中阴影部分的面积与正方形ABCD的面积之比为2∶3,则△BCG的周长为( )
A.7 B.3+ C.8 D.3+
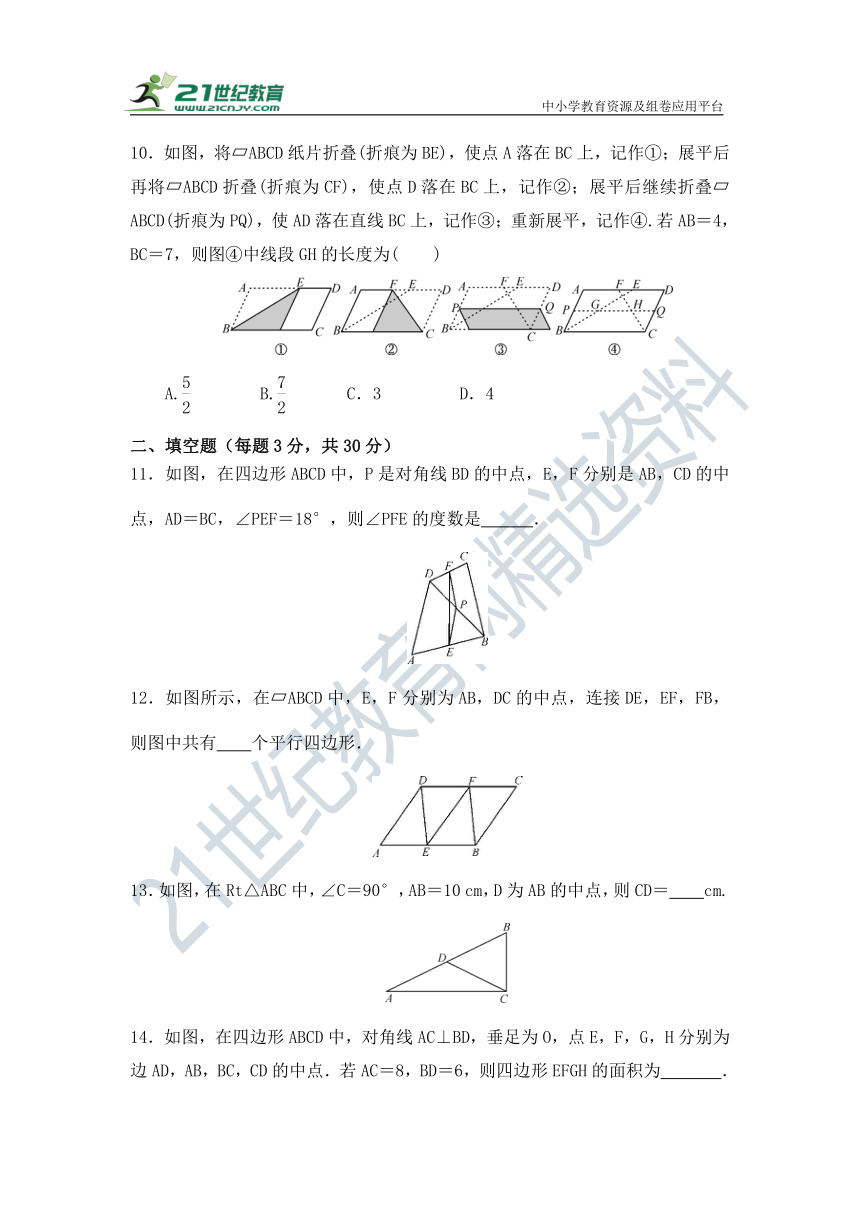
10.如图,将 ABCD纸片折叠(折痕为BE),使点A落在BC上,记作①;展平后再将 ABCD折叠(折痕为CF),使点D落在BC上,记作②;展平后继续折叠 ABCD(折痕为PQ),使AD落在直线BC上,记作③;重新展平,记作④.若AB=4,BC=7,则图④中线段GH的长度为( )
A. B. C.3 D.4
二、填空题(每题3分,共30分)
11.如图,在四边形ABCD中,P是对角线BD的中点,E,F分别是AB,CD的中点,AD=BC,∠PEF=18°,则∠PFE的度数是 .
12.如图所示,在 ABCD中,E,F分别为AB,DC的中点,连接DE,EF,FB,则图中共有 个平行四边形.
13.如图,在Rt△ABC中,∠C=90°,AB=10 cm,D为AB的中点,则CD= cm.
14.如图,在四边形ABCD中,对角线AC⊥BD,垂足为O,点E,F,G,H分别为边AD,AB,BC,CD的中点.若AC=8,BD=6,则四边形EFGH的面积为 .
15.如图,将正方形纸片按如图折叠,AM为折痕,点B落在对角线AC上的点E处,则∠CME= .
16.如图,在正方形ABCD中,以AB为边在正方形内作等边△ABE,连接DE,CE,则∠CED的度数为 .
如图,在矩形ABCD中,点P在对角线AC上,过点P作EF∥BC,分别交AB,CD于点E,连接PB,PD.若PB=2,PD=6,图中阴影部分的面积为9,则矩形ABCD的周长为________.
18.如图,四边形ABDE和四边形ACFG都是正方形,CE与BG交于点M,点M在△ABC的外部.①;②;③.上述结论正确的是__________.
三、解答题(本题共有6小题,共46分)
19.(6分)形ABCD中,点E,F分别在AB,BC上,△DEF为等腰直角三角形,∠DEF=90°,AD+CD=10,AE=2,求AD的长.
20.(8分)如图,平行四边形ABCD中,AB=6cm,BC=10cm,∠B=60°,G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F,连接CE,DF.
(1)求证:四边形CEDF是平行四边形;
(2)以下两问二选一进行求解.
①当AE=____cm时,四边形CEDF是矩形;
②当AE=____cm时,四边形CEDF是菱形.
21、(8分)如图,平行四边形ABCD的对角线交于点O,以OD,CD为邻边作平行四边形DOEC,OE交BC于点F,连结BE.
(1)求证:F为BC中点;
(2)若OB⊥AC,OF=2,求平行四边形ABCD的周长.
22、(8分)如图,AC是矩形ABCD的对角线,过AC的中点O作EF⊥AC,交BC于点E,交AD于点F,连接AE,CF.
(1)求证:四边形AECF是菱形;
(2)若AB=,∠DCF=30°,求四边形AECF的面积.(结果保留根号)
23.如图,把长方形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C′的位置上.
(1)若∠1=55°,求∠2、∠3的度数;
(2)若AB=12,AD=18,求△BC′F的面积.
24.为了庆祝建校八十周年,某校各班都在开展丰富多彩的庆祝活动,八年级(3)班开展了手工制作竞赛,每个同学都在规定时间内完成一件手工作品.陈莉同学制作手工作品的第一、二个步骤是:①先裁下了一张长BC=20 cm,宽AB=16 cm的长方形纸片ABCD;②将纸片沿着直线AE折叠,使点D恰好落在BC边上的F处……请你根据①②步骤解答下列问题.
(1)找出图中的∠FEC的余角;
(2)计算EC的长.
参考答案
选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 D B B A C A C D D C
二.填空题
11.如图,在四边形ABCD中,P是对角线BD的中点,E,F分别是AB,CD的中点,AD=BC,∠PEF=18°,则∠PFE的度数是18°.
12.如图所示,在 ABCD中,E,F分别为AB,DC的中点,连接DE,EF,FB,则图中共有4个平行四边形.
13.如图,在Rt△ABC中,∠C=90°,AB=10 cm,D为AB的中点,则CD=5cm.
14.如图,在四边形ABCD中,对角线AC⊥BD,垂足为O,点E,F,G,H分别为边AD,AB,BC,CD的中点.若AC=8,BD=6,则四边形EFGH的面积为12.
15.如图,将正方形纸片按如图折叠,AM为折痕,点B落在对角线AC上的点E处,则∠CME=45°.
16.如图,在正方形ABCD中,以AB为边在正方形内作等边△ABE,连接DE,CE,则∠CED的度数为150°.
.2+6
18.①②
三、解答题
19.∵四边形ABCD是矩形,∴∠A=∠B=90°.∴∠ADE+∠DEA=90°.∵∠DEF=90°,∴∠DEA+∠BEF=90°.∴∠ADE=∠BEF.∵DE=EF,∴△ADE≌△BEF(AAS).设AD=x,则EB=x,∴AB=2+x.∵AD+CD=10,∴DC=10-x.∵DC=AB,∴10-x=2+x.∴x=4.∴AD=4.
20.(1)证明:∵四边形ABCD是平行四边形,∴CF∥ED,∴∠FCG=∠EDG,∵G是CD的中点,∴CG=DG,∵∠CGF=∠DGE,∴△FCG≌△EDG,∴FG=EG,∵CG=DG,∴四边形CEDF是平行四边形. (2)①当∠CED=90°,∵∠EDC=∠B=60°,∴DE=DC=AB=3cm,∴AE=AD-DE=7cm. ②当DE=CE时,∵∠EDC=∠B=60°,∴△CED是等边三角形,∴DE=CD=AB=6cm,AE=AD-DE=4cm.
21、解:四边形ABCD是平行四边形.
理由:∵A(﹣3,﹣2),B(0,3),C(3,2),D(0,﹣3),
∴AB=CD,BC=AD,
∴四边形ABCD是平行四边形.
22、(1)证明:∵O是AC的中点,且EF⊥AC,
∴AF=CF,AE=CE,OA=OC,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠AFO=∠CEO,
在△AOF和△COE中,
,
∴△AOF≌△COE(AAS),
∴AF=CE,
∴AF=CF=CE=AE,
∴四边形AECF是菱形;
(2)解:∵四边形ABCD是矩形,
∴CD=AB=,
在Rt△CDF中,cos∠DCF=,∠DCF=30°,
∴CF==2,
∵四边形AECF是菱形,
∴CE=CF=2,
∴四边形AECF是的面积为:EC AB=2.
23.(1)∠2=55°,∠3=70°;(2)
24.(1)∠CFE、∠BAF;(2) 6 cm.
《平行四边形》单元测试
题号 一 二 三 总分
19 20 21 22 23 24
分数
一.选择题(每题3分,共30分)
1.下列说法中,错误的是
A.平行四边形的对角线互相平分 B.对角线互相平分的四边形是平行四边
C.菱形的对角线互相垂直 D.对角线互相垂直的四边形是菱形
2.如图所示,在中,,是上的点,交于点,交于点,那么四边形的周长是
A.5 B.10 C.15 D.20
3.如图所示,在中,对角线,交于点,图中全等三角形有
A.5对 B.4对 C.3对 D.2对
4.在平行四边形ABCD中,对角线AC、BD相交于点O,以点O为坐标原点建立平面直角坐标系,其中A(a,b),B(a-1,b+2),C(3,1),则点D的坐标是( )
A.(4,-1) B.(-3,-1) C.(2,3) D.(-4,1)
5.如图,在菱形ABCD中,AC与BD相交于点O,AC=6,BD=8,则菱形边长AB等于( )
A.10 B. C.5 D.6
5题图 6题图 7题图
6.小玲的爸爸在钉制平行四边形框架时,采用了一种方法:如图,将两根木条AC、BD的中点重叠并用钉子固定,则四边形ABCD就是平行四边形,这种方法的依据是( )
A.对角线互相平分的四边形是平行四边形
B.两组对角分别相等的四边形是平行四边形
C.两组对边分别相等的四边形是平行四边形
D.两组对边分别平行的四边形是平行四边形
7.如图,矩形ABCD的两条对角线相交于点O,∠AOD=60°,AD=4,则该矩形的面积是( )
A.16 B.8 C.16 D.8
8.如图所示,在矩形ABCD中,AB=4,AD=3,矩形内部有一动点P满足S△PAB=S矩形ABCD,则点P到A,B两点的距离之和PA+PB的最小值为( )
A.5 B.2 C.2 D.4
9.如图,在正方形ABCD中,AB=3,点E,F分别在CD,AD上,CE=DF,BE,CF相交于点G.若图中阴影部分的面积与正方形ABCD的面积之比为2∶3,则△BCG的周长为( )
A.7 B.3+ C.8 D.3+
10.如图,将 ABCD纸片折叠(折痕为BE),使点A落在BC上,记作①;展平后再将 ABCD折叠(折痕为CF),使点D落在BC上,记作②;展平后继续折叠 ABCD(折痕为PQ),使AD落在直线BC上,记作③;重新展平,记作④.若AB=4,BC=7,则图④中线段GH的长度为( )
A. B. C.3 D.4
二、填空题(每题3分,共30分)
11.如图,在四边形ABCD中,P是对角线BD的中点,E,F分别是AB,CD的中点,AD=BC,∠PEF=18°,则∠PFE的度数是 .
12.如图所示,在 ABCD中,E,F分别为AB,DC的中点,连接DE,EF,FB,则图中共有 个平行四边形.
13.如图,在Rt△ABC中,∠C=90°,AB=10 cm,D为AB的中点,则CD= cm.
14.如图,在四边形ABCD中,对角线AC⊥BD,垂足为O,点E,F,G,H分别为边AD,AB,BC,CD的中点.若AC=8,BD=6,则四边形EFGH的面积为 .
15.如图,将正方形纸片按如图折叠,AM为折痕,点B落在对角线AC上的点E处,则∠CME= .
16.如图,在正方形ABCD中,以AB为边在正方形内作等边△ABE,连接DE,CE,则∠CED的度数为 .
如图,在矩形ABCD中,点P在对角线AC上,过点P作EF∥BC,分别交AB,CD于点E,连接PB,PD.若PB=2,PD=6,图中阴影部分的面积为9,则矩形ABCD的周长为________.
18.如图,四边形ABDE和四边形ACFG都是正方形,CE与BG交于点M,点M在△ABC的外部.①;②;③.上述结论正确的是__________.
三、解答题(本题共有6小题,共46分)
19.(6分)形ABCD中,点E,F分别在AB,BC上,△DEF为等腰直角三角形,∠DEF=90°,AD+CD=10,AE=2,求AD的长.
20.(8分)如图,平行四边形ABCD中,AB=6cm,BC=10cm,∠B=60°,G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F,连接CE,DF.
(1)求证:四边形CEDF是平行四边形;
(2)以下两问二选一进行求解.
①当AE=____cm时,四边形CEDF是矩形;
②当AE=____cm时,四边形CEDF是菱形.
21、(8分)如图,平行四边形ABCD的对角线交于点O,以OD,CD为邻边作平行四边形DOEC,OE交BC于点F,连结BE.
(1)求证:F为BC中点;
(2)若OB⊥AC,OF=2,求平行四边形ABCD的周长.
22、(8分)如图,AC是矩形ABCD的对角线,过AC的中点O作EF⊥AC,交BC于点E,交AD于点F,连接AE,CF.
(1)求证:四边形AECF是菱形;
(2)若AB=,∠DCF=30°,求四边形AECF的面积.(结果保留根号)
23.如图,把长方形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C′的位置上.
(1)若∠1=55°,求∠2、∠3的度数;
(2)若AB=12,AD=18,求△BC′F的面积.
24.为了庆祝建校八十周年,某校各班都在开展丰富多彩的庆祝活动,八年级(3)班开展了手工制作竞赛,每个同学都在规定时间内完成一件手工作品.陈莉同学制作手工作品的第一、二个步骤是:①先裁下了一张长BC=20 cm,宽AB=16 cm的长方形纸片ABCD;②将纸片沿着直线AE折叠,使点D恰好落在BC边上的F处……请你根据①②步骤解答下列问题.
(1)找出图中的∠FEC的余角;
(2)计算EC的长.
参考答案
选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 D B B A C A C D D C
二.填空题
11.如图,在四边形ABCD中,P是对角线BD的中点,E,F分别是AB,CD的中点,AD=BC,∠PEF=18°,则∠PFE的度数是18°.
12.如图所示,在 ABCD中,E,F分别为AB,DC的中点,连接DE,EF,FB,则图中共有4个平行四边形.
13.如图,在Rt△ABC中,∠C=90°,AB=10 cm,D为AB的中点,则CD=5cm.
14.如图,在四边形ABCD中,对角线AC⊥BD,垂足为O,点E,F,G,H分别为边AD,AB,BC,CD的中点.若AC=8,BD=6,则四边形EFGH的面积为12.
15.如图,将正方形纸片按如图折叠,AM为折痕,点B落在对角线AC上的点E处,则∠CME=45°.
16.如图,在正方形ABCD中,以AB为边在正方形内作等边△ABE,连接DE,CE,则∠CED的度数为150°.
.2+6
18.①②
三、解答题
19.∵四边形ABCD是矩形,∴∠A=∠B=90°.∴∠ADE+∠DEA=90°.∵∠DEF=90°,∴∠DEA+∠BEF=90°.∴∠ADE=∠BEF.∵DE=EF,∴△ADE≌△BEF(AAS).设AD=x,则EB=x,∴AB=2+x.∵AD+CD=10,∴DC=10-x.∵DC=AB,∴10-x=2+x.∴x=4.∴AD=4.
20.(1)证明:∵四边形ABCD是平行四边形,∴CF∥ED,∴∠FCG=∠EDG,∵G是CD的中点,∴CG=DG,∵∠CGF=∠DGE,∴△FCG≌△EDG,∴FG=EG,∵CG=DG,∴四边形CEDF是平行四边形. (2)①当∠CED=90°,∵∠EDC=∠B=60°,∴DE=DC=AB=3cm,∴AE=AD-DE=7cm. ②当DE=CE时,∵∠EDC=∠B=60°,∴△CED是等边三角形,∴DE=CD=AB=6cm,AE=AD-DE=4cm.
21、解:四边形ABCD是平行四边形.
理由:∵A(﹣3,﹣2),B(0,3),C(3,2),D(0,﹣3),
∴AB=CD,BC=AD,
∴四边形ABCD是平行四边形.
22、(1)证明:∵O是AC的中点,且EF⊥AC,
∴AF=CF,AE=CE,OA=OC,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠AFO=∠CEO,
在△AOF和△COE中,
,
∴△AOF≌△COE(AAS),
∴AF=CE,
∴AF=CF=CE=AE,
∴四边形AECF是菱形;
(2)解:∵四边形ABCD是矩形,
∴CD=AB=,
在Rt△CDF中,cos∠DCF=,∠DCF=30°,
∴CF==2,
∵四边形AECF是菱形,
∴CE=CF=2,
∴四边形AECF是的面积为:EC AB=2.
23.(1)∠2=55°,∠3=70°;(2)
24.(1)∠CFE、∠BAF;(2) 6 cm.
