北师大版数学七年级下册 1.3.2零指数幂与负整指数幂 课件(共15张PPT)
文档属性
| 名称 | 北师大版数学七年级下册 1.3.2零指数幂与负整指数幂 课件(共15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 399.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-02 00:00:00 | ||
图片预览


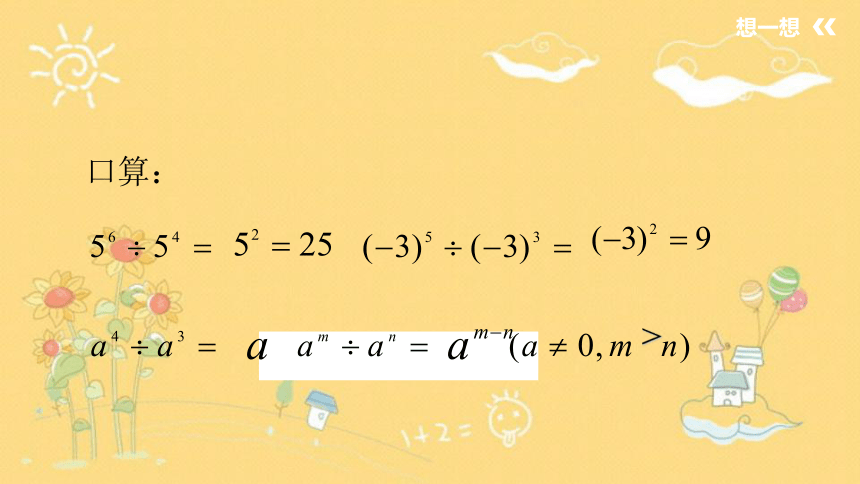



文档简介
(共15张PPT)
第一章 整式的乘除
1.3.2零指数幂与负整指数幂
复习
幂的运算性质:
(1)am·an= ;
(2) (am)n = ;
(3)(ab)n = ;
(4)am÷an = 。
注意:这里的m、n均为正整数。
am+n
am-n
amn
anbn
(m>n,且a≠0)
想一想
>
探索新知
1
1
……
……
1
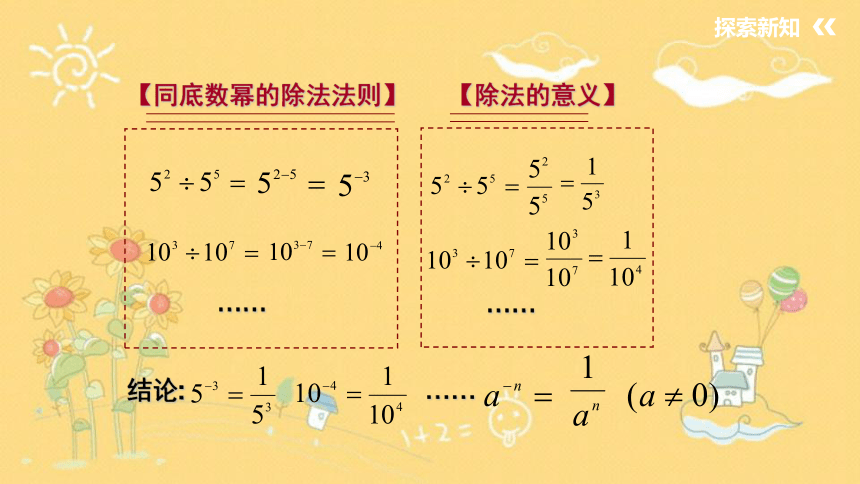
结论:
……
任何不等于零的数的零次幂都等于1.
【同底数幂的除法法则】
【除法的意义】
探索新知
a0 =1
(a 0)
≠
请用语言叙述
由此我们规定
任何不等于零的数的零次幂都等于1。
练:1:
1、计算:
(1)108÷108 (2)(-0.1)0 (3)
(4) (5)
2、想一想,(x-1)0等于什么?
探索新知
……
……
结论:
……
【同底数幂的除法法则】
【除法的意义】
知识归纳
任何不等于零的数的负整数次幂等于它的正整数次幂的倒数.
知识归纳
如何计算负整指数幂:
(a≠0,n是正整数)
两 变
一:负变正 二:求倒数
知识归纳
解:
知识归纳
例 2 用小数表示下列各数:
解:
知识归纳
2
1
1
)
3
2
).(
3
(
)
3
).(
2
(
2
).
1
(
-
-
-
-
对于(1)(2)你有什么发现了吗
对于(3)你作怎样的大胆猜想
例3
计算
知识归纳
初试
练习2:判断
×
√
√
√
√
知识归纳
练习3
1.用小数或分数表示下列各数.
知识归纳
1、计算
练习4
总结
1.我们知道了指数有正整数,还有负整数、零 。
a0 = 1,(a≠0),
a-n= ( a≠0 ,且 n为正整数)
第一章 整式的乘除
1.3.2零指数幂与负整指数幂
复习
幂的运算性质:
(1)am·an= ;
(2) (am)n = ;
(3)(ab)n = ;
(4)am÷an = 。
注意:这里的m、n均为正整数。
am+n
am-n
amn
anbn
(m>n,且a≠0)
想一想
>
探索新知
1
1
……
……
1
结论:
……
任何不等于零的数的零次幂都等于1.
【同底数幂的除法法则】
【除法的意义】
探索新知
a0 =1
(a 0)
≠
请用语言叙述
由此我们规定
任何不等于零的数的零次幂都等于1。
练:1:
1、计算:
(1)108÷108 (2)(-0.1)0 (3)
(4) (5)
2、想一想,(x-1)0等于什么?
探索新知
……
……
结论:
……
【同底数幂的除法法则】
【除法的意义】
知识归纳
任何不等于零的数的负整数次幂等于它的正整数次幂的倒数.
知识归纳
如何计算负整指数幂:
(a≠0,n是正整数)
两 变
一:负变正 二:求倒数
知识归纳
解:
知识归纳
例 2 用小数表示下列各数:
解:
知识归纳
2
1
1
)
3
2
).(
3
(
)
3
).(
2
(
2
).
1
(
-
-
-
-
对于(1)(2)你有什么发现了吗
对于(3)你作怎样的大胆猜想
例3
计算
知识归纳
初试
练习2:判断
×
√
√
√
√
知识归纳
练习3
1.用小数或分数表示下列各数.
知识归纳
1、计算
练习4
总结
1.我们知道了指数有正整数,还有负整数、零 。
a0 = 1,(a≠0),
a-n= ( a≠0 ,且 n为正整数)
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
