沪科版数学七年级下册 10.2 第4课时 平行线的判定方法2,3 同步课件(共15张PPT)
文档属性
| 名称 | 沪科版数学七年级下册 10.2 第4课时 平行线的判定方法2,3 同步课件(共15张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 487.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-02 07:58:42 | ||
图片预览




文档简介
(共15张PPT)
10.2 第4课时 平行线的判定方法2,3
第10章 相交线、平行线与平移
情景引入
两条直线被第三条直线所截,由同位角相等可以判定两条直线平行,那么内错角相等可以判定两条直线平行吗?同旁内角互补呢?
如图,已知∠1=∠2,AB与CD平行吗?为什么?
A
B
C
D
E
F
1
2
3
∵∠1 =∠2(已知),
∠2 =∠3(对顶角相等),
∴∠1 =∠3.
AB∥CD
(同位角相等,两直线平行).
获取新知
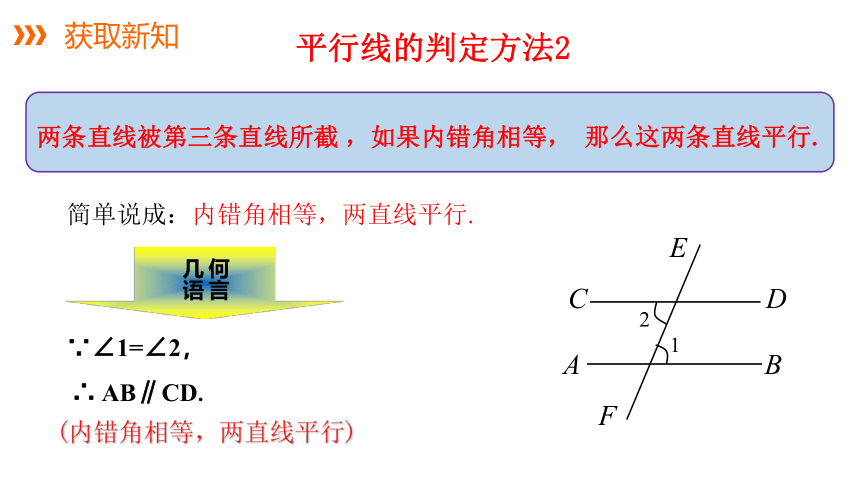
平行线的判定方法2
简单说成:内错角相等,两直线平行.
何言
几语
(内错角相等,两直线平行)
A
B
C
D
E
F
1
2
∵∠1=∠2,
∴ AB∥CD.
两条直线被第三条直线所截 ,如果内错角相等, 那么这两条直线平行.
获取新知
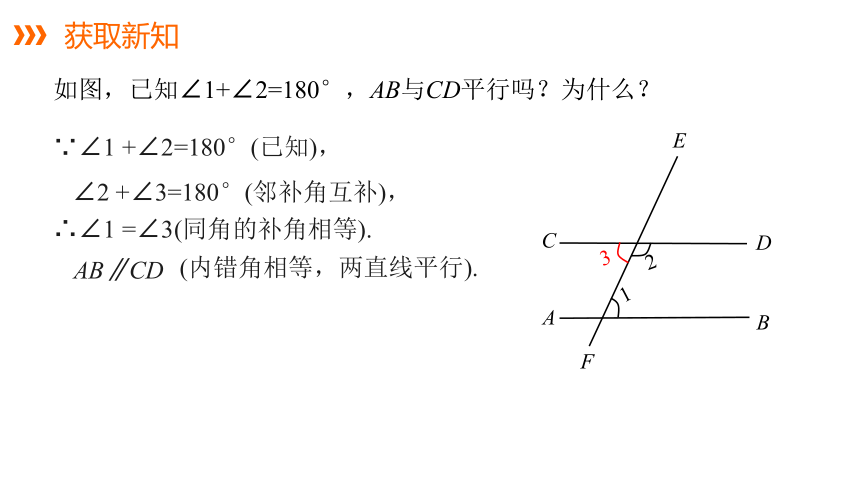
如图,已知∠1+∠2=180°,AB与CD平行吗?为什么?
A
B
C
D
E
F
1
2
∵∠1 +∠2=180°(已知),
∠2 +∠3=180°(邻补角互补),
∴∠1 =∠3(同角的补角相等).
AB∥CD
(内错角相等,两直线平行).
3
获取新知
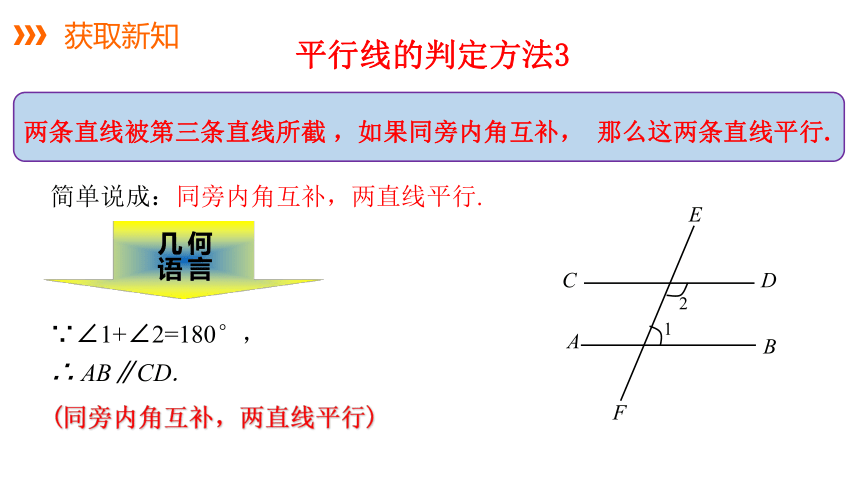
平行线的判定方法3
简单说成:同旁内角互补,两直线平行.
何言
几语
(同旁内角互补,两直线平行)
A
B
C
D
E
F
1
2
∵∠1+∠2=180°,
∴ AB∥CD.
两条直线被第三条直线所截 ,如果同旁内角互补, 那么这两条直线平行.
获取新知
如图:∠B=∠D=45°,∠C=135°,问图中有哪些直线平行?
答:AB//CD,AD//BC
∵∠B=45°(已知)
∠C=135°(已知)
∴ ∠B+ ∠C=180°
AB//CD(同旁内角互补,两直线平行)
同理:AD//BC.
D
C
B
A
例题讲解
例3 如图,AB∥DC,∠BAD=∠BCD.那么AD∥BC吗?
解 因为AB∥DC,
所以∠1=∠2
(两直线平行,内错角相等).
又因为∠BAD=∠BCD,
所以∠BAD-∠1=∠BCD-∠2.
即 ∠3=∠4.
所以 AD∥BC(内错角相等,两直线平行).
例题讲解
解 因为AD∥BC,
所以∠1+∠3=180°
(两直线平行,同旁内角互补)
所以 AB∥DC(同旁内角互补,两直线平行).
例4 如图,∠1=∠2=50°, AD∥BC,那么AB∥DC吗?
例题讲解
【归纳总结】利用“同旁内角互补,两直线平行”判定两直线平行的方法
①看互补的两角有无公共边,若有,则以这条公共边所在的直线为截线,然后以这条截线为线索寻找其他两条直线;②看互补的两角是不是上述直线形成的同旁内角,若是,则这两条直线平行.
随堂演练
1.如图,∠5=70°,在给出的下列条件中,不能判定AB∥CD的是( )
A.∠2= 70° B.∠3= 110°
C.∠4= 110° D.∠1= 70°
C
2.(天门·中考)对于图中标记的各角,通过下列条件能够推理得到a∥b的是( )
A.∠1=∠2 B.∠2=∠4
C.∠3=∠4 D.∠1+∠4=180°
【解析】选D.∠1的对顶角与∠4是直线a,b被一条直线所截而成的同旁内角,所以当∠1+∠4=180°时,a∥b.
随堂演练
AB
CD
内错角相等,两直线平行
AC
BD
内错角相等,两直线平行
AC
BD
同旁内角互补,两直线平行
随堂演练
C
A
随堂演练
C
7.如图1所示,下列条件中,不能判断直线a∥b的是( ).
A.∠1=∠3 B.∠2=∠3
C.∠4=∠5 D. ∠2+∠4=180°
B
图1
随堂演练
课后小结
判定两条直线平行的方法
文字叙述 符号语言 图形
相等 两直线平行 ∵ (已知), ∴a∥b
相等 两直线平行 ∵ (已知), ∴a∥b 互补,两直线平行 ∵ (已知),∴a∥b 同位角
内错角
同旁内角
∠1=∠2
∠3=∠2
∠2+∠4=180°
a
b
c
1
2
3
4
10.2 第4课时 平行线的判定方法2,3
第10章 相交线、平行线与平移
情景引入
两条直线被第三条直线所截,由同位角相等可以判定两条直线平行,那么内错角相等可以判定两条直线平行吗?同旁内角互补呢?
如图,已知∠1=∠2,AB与CD平行吗?为什么?
A
B
C
D
E
F
1
2
3
∵∠1 =∠2(已知),
∠2 =∠3(对顶角相等),
∴∠1 =∠3.
AB∥CD
(同位角相等,两直线平行).
获取新知
平行线的判定方法2
简单说成:内错角相等,两直线平行.
何言
几语
(内错角相等,两直线平行)
A
B
C
D
E
F
1
2
∵∠1=∠2,
∴ AB∥CD.
两条直线被第三条直线所截 ,如果内错角相等, 那么这两条直线平行.
获取新知
如图,已知∠1+∠2=180°,AB与CD平行吗?为什么?
A
B
C
D
E
F
1
2
∵∠1 +∠2=180°(已知),
∠2 +∠3=180°(邻补角互补),
∴∠1 =∠3(同角的补角相等).
AB∥CD
(内错角相等,两直线平行).
3
获取新知
平行线的判定方法3
简单说成:同旁内角互补,两直线平行.
何言
几语
(同旁内角互补,两直线平行)
A
B
C
D
E
F
1
2
∵∠1+∠2=180°,
∴ AB∥CD.
两条直线被第三条直线所截 ,如果同旁内角互补, 那么这两条直线平行.
获取新知
如图:∠B=∠D=45°,∠C=135°,问图中有哪些直线平行?
答:AB//CD,AD//BC
∵∠B=45°(已知)
∠C=135°(已知)
∴ ∠B+ ∠C=180°
AB//CD(同旁内角互补,两直线平行)
同理:AD//BC.
D
C
B
A
例题讲解
例3 如图,AB∥DC,∠BAD=∠BCD.那么AD∥BC吗?
解 因为AB∥DC,
所以∠1=∠2
(两直线平行,内错角相等).
又因为∠BAD=∠BCD,
所以∠BAD-∠1=∠BCD-∠2.
即 ∠3=∠4.
所以 AD∥BC(内错角相等,两直线平行).
例题讲解
解 因为AD∥BC,
所以∠1+∠3=180°
(两直线平行,同旁内角互补)
所以 AB∥DC(同旁内角互补,两直线平行).
例4 如图,∠1=∠2=50°, AD∥BC,那么AB∥DC吗?
例题讲解
【归纳总结】利用“同旁内角互补,两直线平行”判定两直线平行的方法
①看互补的两角有无公共边,若有,则以这条公共边所在的直线为截线,然后以这条截线为线索寻找其他两条直线;②看互补的两角是不是上述直线形成的同旁内角,若是,则这两条直线平行.
随堂演练
1.如图,∠5=70°,在给出的下列条件中,不能判定AB∥CD的是( )
A.∠2= 70° B.∠3= 110°
C.∠4= 110° D.∠1= 70°
C
2.(天门·中考)对于图中标记的各角,通过下列条件能够推理得到a∥b的是( )
A.∠1=∠2 B.∠2=∠4
C.∠3=∠4 D.∠1+∠4=180°
【解析】选D.∠1的对顶角与∠4是直线a,b被一条直线所截而成的同旁内角,所以当∠1+∠4=180°时,a∥b.
随堂演练
AB
CD
内错角相等,两直线平行
AC
BD
内错角相等,两直线平行
AC
BD
同旁内角互补,两直线平行
随堂演练
C
A
随堂演练
C
7.如图1所示,下列条件中,不能判断直线a∥b的是( ).
A.∠1=∠3 B.∠2=∠3
C.∠4=∠5 D. ∠2+∠4=180°
B
图1
随堂演练
课后小结
判定两条直线平行的方法
文字叙述 符号语言 图形
相等 两直线平行 ∵ (已知), ∴a∥b
相等 两直线平行 ∵ (已知), ∴a∥b 互补,两直线平行 ∵ (已知),∴a∥b 同位角
内错角
同旁内角
∠1=∠2
∠3=∠2
∠2+∠4=180°
a
b
c
1
2
3
4
