沪科版数学七年级下册 10.4 平移 同步课件(共23张PPT)
文档属性
| 名称 | 沪科版数学七年级下册 10.4 平移 同步课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 645.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-02 00:00:00 | ||
图片预览




文档简介
(共23张PPT)
10.4 平移
第10章 相交线、平行线与平移
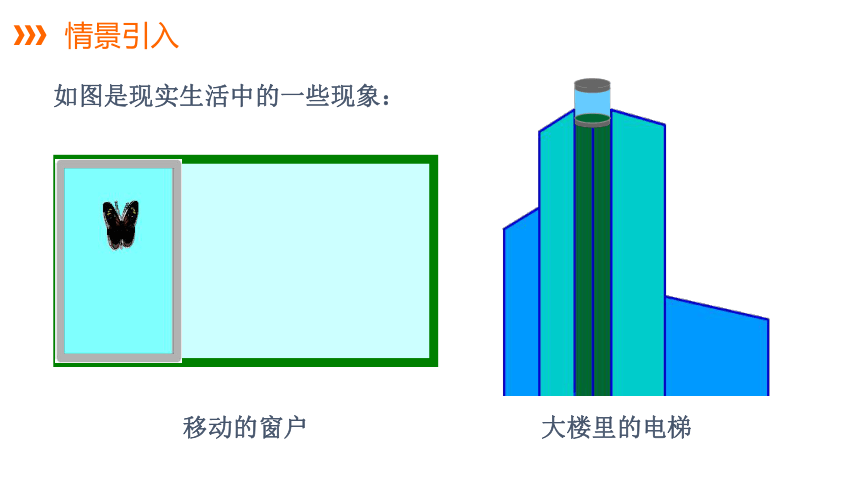
情景引入
如图是现实生活中的一些现象:
移动的窗户
大楼里的电梯
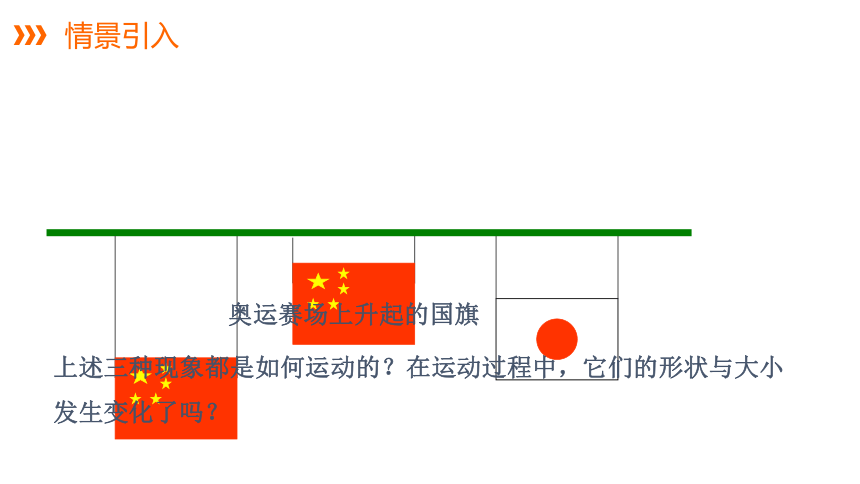
情景引入
奥运赛场上升起的国旗
上述三种现象都是如何运动的?在运动过程中,它们的形状与大小发生变化了吗?
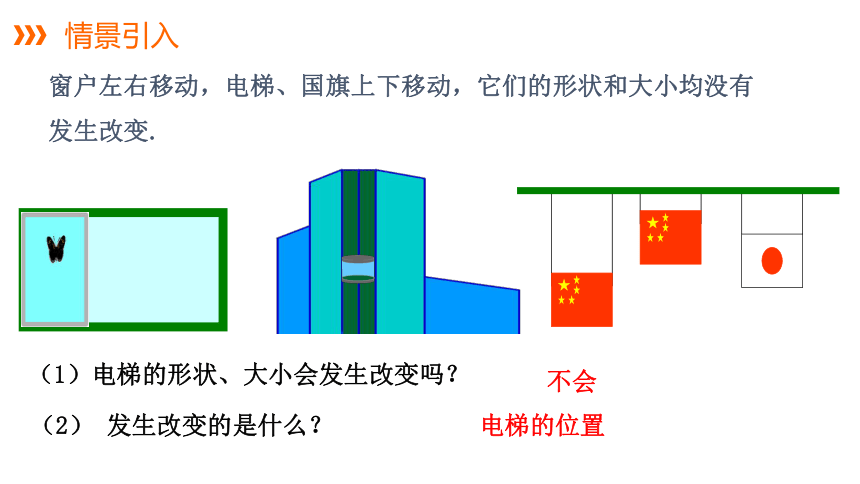
情景引入
窗户左右移动,电梯、国旗上下移动,它们的形状和大小均没有发生改变.
(1)电梯的形状、大小会发生改变吗?
(2) 发生改变的是什么?
不会
电梯的位置
获取新知
知识点一:平移的概念
平移的概念:在平面内,一个图形沿某个方向移动一定的距离,这种图形的变换叫做平移.平移时,原图形上的所有点都沿同一个方向移动相同的距离.原图形上一点A平移后成为点A',这样的两点叫做对应点.
平移的要素:1.移动的方向;
2.移动的距离
图形的平移不一定是水平的,
也不一定是竖直的.
例题讲解
例1 以下现象:①打开教室的门时,门的移动;②打气筒打气时,活塞的运动;③钟摆的摆动;④传送带上,瓶装饮料的移动,其中属于平移的是( )
A.①② B.①③
C.②③ D.②④
D
知2-导
(来自《教材》)
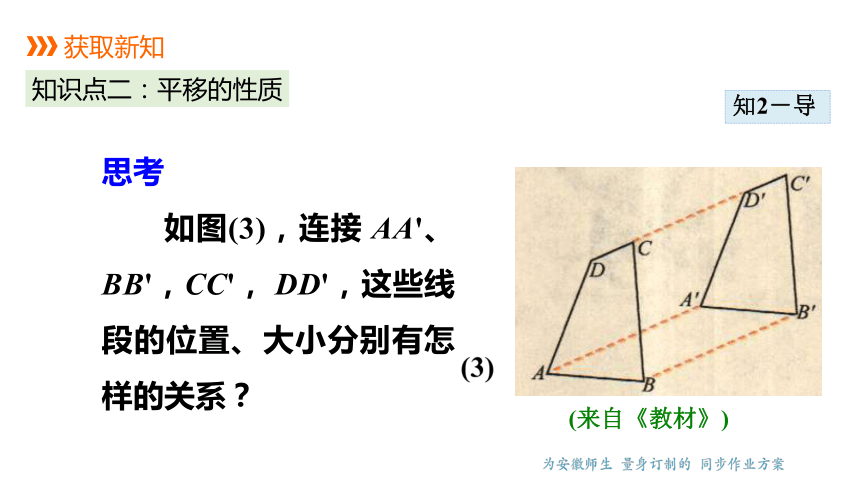
思考
如图(3),连接 AA'、BB',CC', DD',这些线段的位置、大小分别有怎样的关系?
获取新知
知识点二:平移的性质
1. 一个图形和它经过平移后得到的图形中,连接各组对应点的线段互相平行(或在同一直线上)且相等.
2. 平移只改变图形的位置,不改变图形的形状和大小.
归 纳
要点精析:
(1)连接对应点的线段的长度就是平移距离;
(2)从原图上一点到其对应点的方向即起始点到终止点的方向为平移方向.
(3)平移前后图形的对应边平行(或在同一直线上)且相等,对应角相等.
例2 如图,图形中有两个梯形ABCD和EFGH,其中梯形EFGH是由梯形ABCD向右平移2 cm后得到的,问:
(1)线段AE,BF,CG,DH之间有什么数量关系?
(2)AB与EF,BC与FG,CD与GH,AD与EH之间有什么关系?
(3)∠BAD与∠FEH,∠ABC与∠EFG,∠BCD与∠FGH,∠CDA与∠GHE之间有什么数量关系?
例题讲解
解:(1)线段AE,BF,CG,DH的长度相等,都为2 cm.
(2)AB与EF,BC与FG,CD与GH,AD与EH分别平行且相等.
(3)∠BAD与∠FEH,∠ABC与∠EFG,∠BCD与∠FGH,∠CDA与∠GHE对应相等.
例题讲解
例3 如图,平移三角形ABC,使点A移动到点A',
画出平移后的三角形A'B'C'.
A
B
C
A
分析:图形平移后的对应点有什么特征 作出点B和点C的对应点B',C',能确定△A'B'C'吗?
解:如图,连接AA',过点B作
AA'的平行线l,在l上截取BB'=AA',
则点B'就是点B的对应点.
A
B
C
A
B
l
类似地,作出点C的对应点C',并进一步得到平移后的三角形A'B'C' .
A
B
C
A
C
B
l
随堂演练
1.下列生活中的物体的运动情况可以看成平移的是( )
A.篮球运动员投篮时篮球的运动
B.飞机在跑道上滑行到停止的运动
C.空中放飞的风筝的运动
D.冷水加热过程中小气泡上升变为大气泡
B
2. 将如图所示的图案平移后,可以得到的图案是( )
A
3. 如图,将三角形ABC平移可得到三角形A′B′C′,则图中平行线共有( )
A.3对
B.4对
C.5对
D.6对
D
4. 如图,将三角形ABC 沿直线AB向右平移后到达三角形BDE的位置.若∠CAB=50°,∠ABC=100°,则∠CBE的度数为 .
50°
5. 如图,将三角形ABC沿BC方向平移至三角形DEF处.
若EC=2BE=2,则CF的长为 .
1
6.如图,经过平移,四边形ABCD的顶点A移动到点A′,
作出平移后的四边形.
A
B
C
D
A′
D′
C′
B′
7. 如图,在三角形ABC中,AC=4 cm,BC=3 cm,将三角形ABC沿AB方向向右平移得到三角形DEF,若AE=8 cm,DB=2 cm.
(1)求三角形ABC向右平移的距离AD的长;
(2)求四边形AEFC的周长.
解:(1)∵三角形ABC沿AB方向向右平移得到三角形DEF,
∴AD=BE=CF,BC=EF=3 cm.
∵AE=8 cm,DB=2 cm,
∴AD=BE=CF= ×(8-2)=3(cm).
(2)四边形AEFC的周长 =AE+EF+CF+AC=8+3+3+4=18(cm).
课堂小结
平移前后图形的形状和大小,完全相同
对应线段平行(或在同一直线上)且相等,对应角相等
平移的概念
平移的性质
平移
各对应点所连线段平行(或在同一直线上)且相等
10.4 平移
第10章 相交线、平行线与平移
情景引入
如图是现实生活中的一些现象:
移动的窗户
大楼里的电梯
情景引入
奥运赛场上升起的国旗
上述三种现象都是如何运动的?在运动过程中,它们的形状与大小发生变化了吗?
情景引入
窗户左右移动,电梯、国旗上下移动,它们的形状和大小均没有发生改变.
(1)电梯的形状、大小会发生改变吗?
(2) 发生改变的是什么?
不会
电梯的位置
获取新知
知识点一:平移的概念
平移的概念:在平面内,一个图形沿某个方向移动一定的距离,这种图形的变换叫做平移.平移时,原图形上的所有点都沿同一个方向移动相同的距离.原图形上一点A平移后成为点A',这样的两点叫做对应点.
平移的要素:1.移动的方向;
2.移动的距离
图形的平移不一定是水平的,
也不一定是竖直的.
例题讲解
例1 以下现象:①打开教室的门时,门的移动;②打气筒打气时,活塞的运动;③钟摆的摆动;④传送带上,瓶装饮料的移动,其中属于平移的是( )
A.①② B.①③
C.②③ D.②④
D
知2-导
(来自《教材》)
思考
如图(3),连接 AA'、BB',CC', DD',这些线段的位置、大小分别有怎样的关系?
获取新知
知识点二:平移的性质
1. 一个图形和它经过平移后得到的图形中,连接各组对应点的线段互相平行(或在同一直线上)且相等.
2. 平移只改变图形的位置,不改变图形的形状和大小.
归 纳
要点精析:
(1)连接对应点的线段的长度就是平移距离;
(2)从原图上一点到其对应点的方向即起始点到终止点的方向为平移方向.
(3)平移前后图形的对应边平行(或在同一直线上)且相等,对应角相等.
例2 如图,图形中有两个梯形ABCD和EFGH,其中梯形EFGH是由梯形ABCD向右平移2 cm后得到的,问:
(1)线段AE,BF,CG,DH之间有什么数量关系?
(2)AB与EF,BC与FG,CD与GH,AD与EH之间有什么关系?
(3)∠BAD与∠FEH,∠ABC与∠EFG,∠BCD与∠FGH,∠CDA与∠GHE之间有什么数量关系?
例题讲解
解:(1)线段AE,BF,CG,DH的长度相等,都为2 cm.
(2)AB与EF,BC与FG,CD与GH,AD与EH分别平行且相等.
(3)∠BAD与∠FEH,∠ABC与∠EFG,∠BCD与∠FGH,∠CDA与∠GHE对应相等.
例题讲解
例3 如图,平移三角形ABC,使点A移动到点A',
画出平移后的三角形A'B'C'.
A
B
C
A
分析:图形平移后的对应点有什么特征 作出点B和点C的对应点B',C',能确定△A'B'C'吗?
解:如图,连接AA',过点B作
AA'的平行线l,在l上截取BB'=AA',
则点B'就是点B的对应点.
A
B
C
A
B
l
类似地,作出点C的对应点C',并进一步得到平移后的三角形A'B'C' .
A
B
C
A
C
B
l
随堂演练
1.下列生活中的物体的运动情况可以看成平移的是( )
A.篮球运动员投篮时篮球的运动
B.飞机在跑道上滑行到停止的运动
C.空中放飞的风筝的运动
D.冷水加热过程中小气泡上升变为大气泡
B
2. 将如图所示的图案平移后,可以得到的图案是( )
A
3. 如图,将三角形ABC平移可得到三角形A′B′C′,则图中平行线共有( )
A.3对
B.4对
C.5对
D.6对
D
4. 如图,将三角形ABC 沿直线AB向右平移后到达三角形BDE的位置.若∠CAB=50°,∠ABC=100°,则∠CBE的度数为 .
50°
5. 如图,将三角形ABC沿BC方向平移至三角形DEF处.
若EC=2BE=2,则CF的长为 .
1
6.如图,经过平移,四边形ABCD的顶点A移动到点A′,
作出平移后的四边形.
A
B
C
D
A′
D′
C′
B′
7. 如图,在三角形ABC中,AC=4 cm,BC=3 cm,将三角形ABC沿AB方向向右平移得到三角形DEF,若AE=8 cm,DB=2 cm.
(1)求三角形ABC向右平移的距离AD的长;
(2)求四边形AEFC的周长.
解:(1)∵三角形ABC沿AB方向向右平移得到三角形DEF,
∴AD=BE=CF,BC=EF=3 cm.
∵AE=8 cm,DB=2 cm,
∴AD=BE=CF= ×(8-2)=3(cm).
(2)四边形AEFC的周长 =AE+EF+CF+AC=8+3+3+4=18(cm).
课堂小结
平移前后图形的形状和大小,完全相同
对应线段平行(或在同一直线上)且相等,对应角相等
平移的概念
平移的性质
平移
各对应点所连线段平行(或在同一直线上)且相等
