沪科版数学七年级下册 8.1 第4课时 同底数幂的除法 课件(共16张PPT)
文档属性
| 名称 | 沪科版数学七年级下册 8.1 第4课时 同底数幂的除法 课件(共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 150.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-02 08:04:04 | ||
图片预览




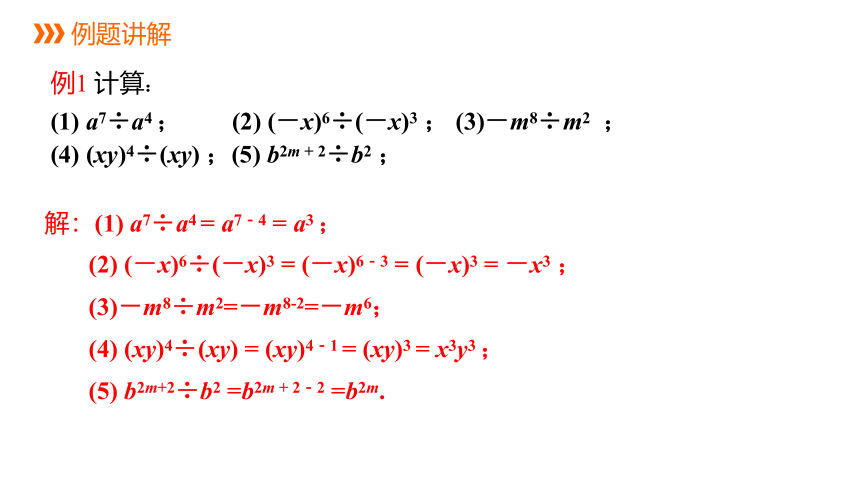
文档简介
(共16张PPT)
第8章 整式乘法与因式分解
8.1 第4课时 同底数幂的除法
知识回顾
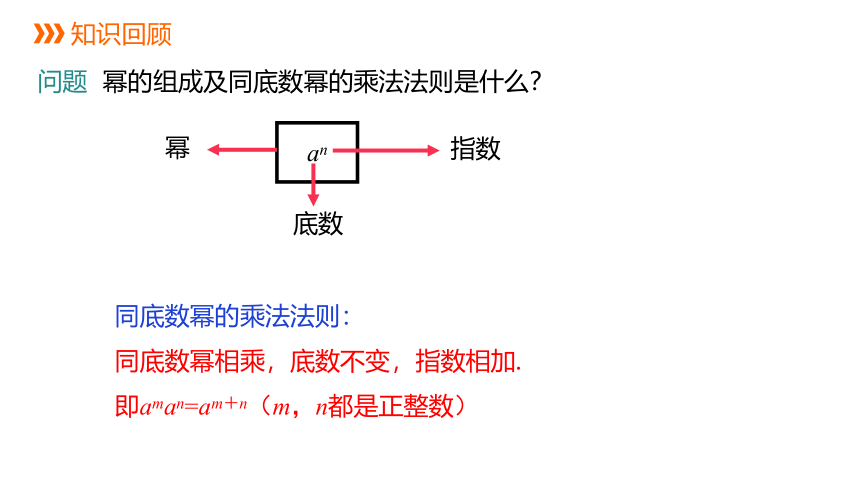
问题 幂的组成及同底数幂的乘法法则是什么?
同底数幂的乘法法则:
同底数幂相乘,底数不变,指数相加.
即aman=am+n(m,n都是正整数)
an
底数
幂
指数
1. 同底数幂相乘,底数不变,指数相加.
2. 幂的乘方,底数不变,指数相乘.
3. 积的乘方,等于每一个因式乘方的积 .
获取新知
怎样计算am÷an
先完成右表:
算式 运算过程 结果
35÷32 33
46÷43
a4÷a2
a5÷a3
43
a2
a2
观察上表,发现幂的乘方有什么规律?
猜想:am÷an=am-n(a≠0,m,n都是正整数,且m>n)
验证:am÷an=
m个a
n个a
=(a·a· ··· ·a)
=am-n
(m-n)个a
归纳总结
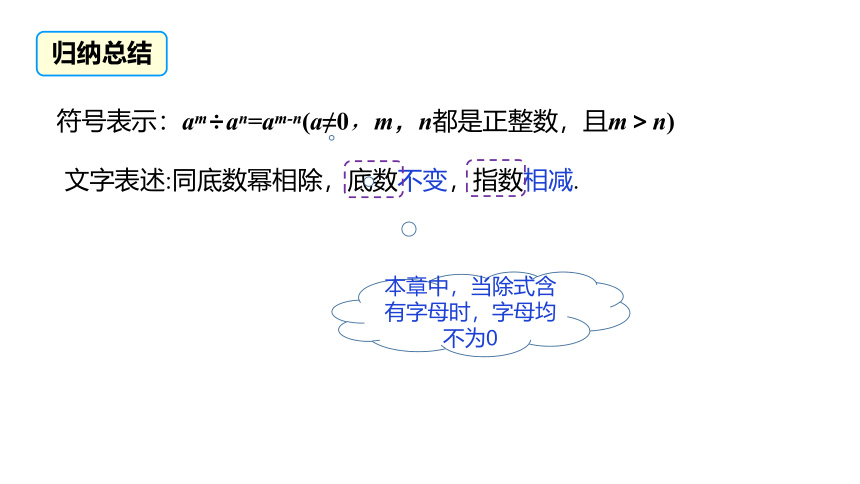
符号表示:am÷an=am-n(a≠0,m,n都是正整数,且m>n)
文字表述:同底数幂相除,底数不变,指数相减.
本章中,当除式含有字母时,字母均不为0
例题讲解
例1 计算:
(1) a7÷a4 ; (2) (-x)6÷(-x)3 ; (3)-m8÷m2 ; (4) (xy)4÷(xy) ;(5) b2m + 2÷b2 ;
解:(1) a7÷a4 = a7-4 = a3 ;
(2) (-x)6÷(-x)3 = (-x)6-3 = (-x)3 = -x3 ;
(3)-m8÷m2=-m8-2=-m6;
(4) (xy)4÷(xy) = (xy)4-1 = (xy)3 = x3y3 ;
(5) b2m+2÷b2 =b2m + 2-2 =b2m.
例2 已知xm=9,xn=27,求x3m-2n的值.
解:x3m-2n=x3m÷x2n=(xm)3÷(xn)2=93÷272=1.
例3 计算:(1)[(a2)5·(-a2)3]÷(-a4)3;
(2)(a-b)3÷(b-a)2+(-a-b)5÷(a+b)4.
分析:按顺序先乘方再乘除,最后加减
解:(1)原式=[a10·(-a6)]÷(-a12)=-a16÷(-a12)
=a16-12=a4.
(2)原式=(a-b)3÷(a-b)2-(a+b)5÷(a+b)4
=(a-b)-(a+b)=a-b-a-b=-2b.
随堂演练
1. 计算x6÷x2正确的结果是( )
A.3 B.x3
C.x4 D.x8
C
2. 下列计算正确的是( )
A.(a2b)2=a2b2
B.a6÷a2=a3
C.(3xy2)2=6x2y4
D.(-m)7÷(-m)2=-m5
D
3. 如果xm=3,xn=2,那么xm-n的值是( )
A.1.5 B.6 C.8 D.9
A
4.(1)若xm+n÷xn=x3,则m=____.
(2)计算:b2m+2÷bm-1=________.
3
m+3
5. 计算:
(1)a5÷a4·a2. (2)(-x)7÷x2.
(3)(ab)5÷(ab)2. (4)(a+b)6÷(a+b)4.
解:(1)a5÷a4·a2=a5-4·a2=a3.
(2)(-x)7÷x2=(-x)7÷(-x)2= (-x)7-2=-x5.
(3)(ab)5÷(ab)2=(ab)5-2=(ab)3=a3b3.
(4)(a+b)6÷(a+b)4=(a+b)6-4=(a+b)2=a2+2ab+b2.
6.已知3m=2, 9n=10, 求33m-2n 的值.
解: 33m-2n =33m÷32n
=(3m)3÷(32)n
=(3m)3÷9n
=23÷10
=8÷10
=0.8
课堂小结
同底数幂的除法
法则
am ÷an=am-n(a ≠0,m,n都是正整数,且m>n)
同底数幂相除,底数不变,指数相减
同底数幂除法法则的逆用:
am-n=am÷an(a ≠0,m,n都是正整数,且m>n)
第8章 整式乘法与因式分解
8.1 第4课时 同底数幂的除法
知识回顾
问题 幂的组成及同底数幂的乘法法则是什么?
同底数幂的乘法法则:
同底数幂相乘,底数不变,指数相加.
即aman=am+n(m,n都是正整数)
an
底数
幂
指数
1. 同底数幂相乘,底数不变,指数相加.
2. 幂的乘方,底数不变,指数相乘.
3. 积的乘方,等于每一个因式乘方的积 .
获取新知
怎样计算am÷an
先完成右表:
算式 运算过程 结果
35÷32 33
46÷43
a4÷a2
a5÷a3
43
a2
a2
观察上表,发现幂的乘方有什么规律?
猜想:am÷an=am-n(a≠0,m,n都是正整数,且m>n)
验证:am÷an=
m个a
n个a
=(a·a· ··· ·a)
=am-n
(m-n)个a
归纳总结
符号表示:am÷an=am-n(a≠0,m,n都是正整数,且m>n)
文字表述:同底数幂相除,底数不变,指数相减.
本章中,当除式含有字母时,字母均不为0
例题讲解
例1 计算:
(1) a7÷a4 ; (2) (-x)6÷(-x)3 ; (3)-m8÷m2 ; (4) (xy)4÷(xy) ;(5) b2m + 2÷b2 ;
解:(1) a7÷a4 = a7-4 = a3 ;
(2) (-x)6÷(-x)3 = (-x)6-3 = (-x)3 = -x3 ;
(3)-m8÷m2=-m8-2=-m6;
(4) (xy)4÷(xy) = (xy)4-1 = (xy)3 = x3y3 ;
(5) b2m+2÷b2 =b2m + 2-2 =b2m.
例2 已知xm=9,xn=27,求x3m-2n的值.
解:x3m-2n=x3m÷x2n=(xm)3÷(xn)2=93÷272=1.
例3 计算:(1)[(a2)5·(-a2)3]÷(-a4)3;
(2)(a-b)3÷(b-a)2+(-a-b)5÷(a+b)4.
分析:按顺序先乘方再乘除,最后加减
解:(1)原式=[a10·(-a6)]÷(-a12)=-a16÷(-a12)
=a16-12=a4.
(2)原式=(a-b)3÷(a-b)2-(a+b)5÷(a+b)4
=(a-b)-(a+b)=a-b-a-b=-2b.
随堂演练
1. 计算x6÷x2正确的结果是( )
A.3 B.x3
C.x4 D.x8
C
2. 下列计算正确的是( )
A.(a2b)2=a2b2
B.a6÷a2=a3
C.(3xy2)2=6x2y4
D.(-m)7÷(-m)2=-m5
D
3. 如果xm=3,xn=2,那么xm-n的值是( )
A.1.5 B.6 C.8 D.9
A
4.(1)若xm+n÷xn=x3,则m=____.
(2)计算:b2m+2÷bm-1=________.
3
m+3
5. 计算:
(1)a5÷a4·a2. (2)(-x)7÷x2.
(3)(ab)5÷(ab)2. (4)(a+b)6÷(a+b)4.
解:(1)a5÷a4·a2=a5-4·a2=a3.
(2)(-x)7÷x2=(-x)7÷(-x)2= (-x)7-2=-x5.
(3)(ab)5÷(ab)2=(ab)5-2=(ab)3=a3b3.
(4)(a+b)6÷(a+b)4=(a+b)6-4=(a+b)2=a2+2ab+b2.
6.已知3m=2, 9n=10, 求33m-2n 的值.
解: 33m-2n =33m÷32n
=(3m)3÷(32)n
=(3m)3÷9n
=23÷10
=8÷10
=0.8
课堂小结
同底数幂的除法
法则
am ÷an=am-n(a ≠0,m,n都是正整数,且m>n)
同底数幂相除,底数不变,指数相减
同底数幂除法法则的逆用:
am-n=am÷an(a ≠0,m,n都是正整数,且m>n)
