沪科版数学七年级下册 8.1 第1课时 同底数幂的乘法 课件(共17张PPT)
文档属性
| 名称 | 沪科版数学七年级下册 8.1 第1课时 同底数幂的乘法 课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 189.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-02 08:25:10 | ||
图片预览




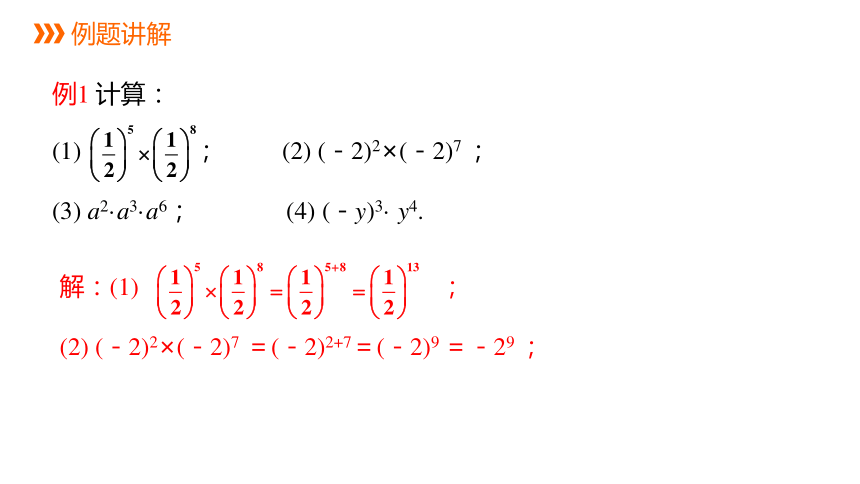
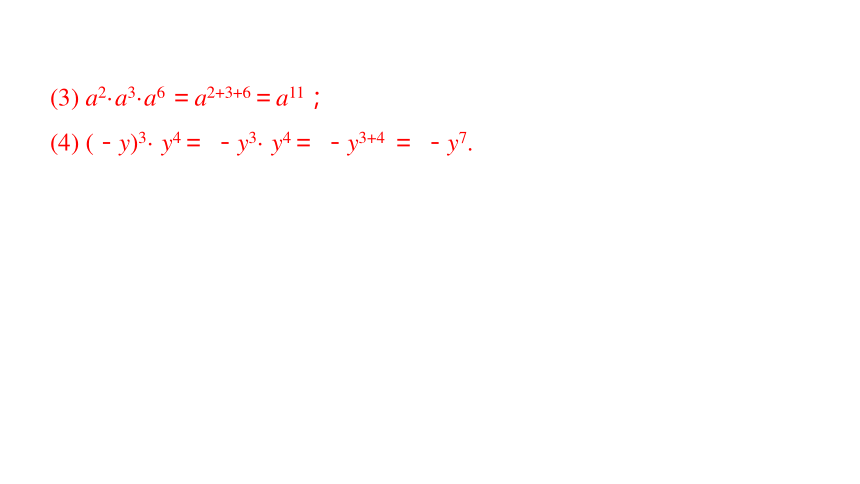
文档简介
(共17张PPT)
第8章 整式乘法与因式分解
8.1 第1课时 同底数幂的乘法
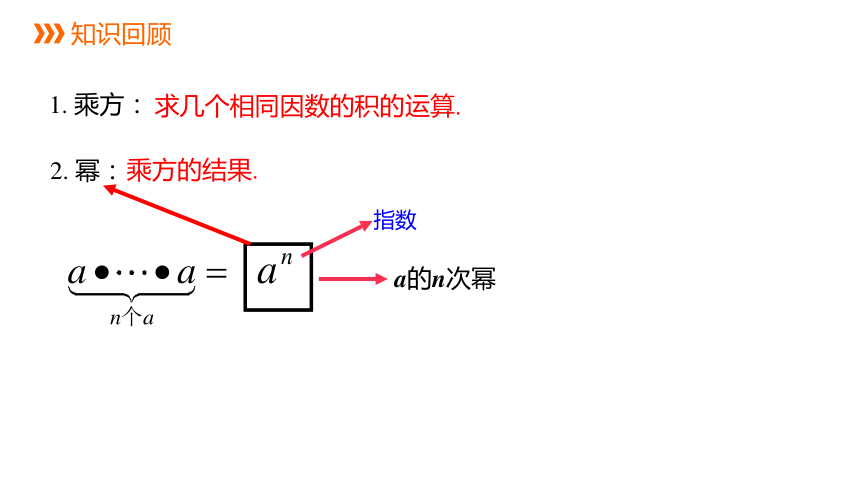
知识回顾
求几个相同因数的积的运算.
1. 乘方:
2. 幂:
乘方的结果.
指数
a的n次幂
获取新知
问题 我国首台千万亿次超级计算机系统“天河一号” 计算机每秒可进行2.57×1015次运算,问它工作1 h (3.6×103 s)可进行多少次运算?
2.57×1015× 3.6×103
=2.57× 3.6×1015×103
=?
解决这个问题需要研究同底数幂的乘法.
观察上表,发现同底数幂相乘有什么规律
算式 运算过程 结果
22×23 2×2×2×2×2 25
103×104
a2 a3
a4 a5
怎样计算,am an
先完成下表:
10×10×10×10×10×10×10
a·a·a·a·a
a·a·a·a·a·a·a·a·a
a5
a9
107
总结归纳
am an = (a a … a) (a a … a)
=a a … a
=am+n
m 个 a
n 个 a
(m+n)个 a
符号表示:am an =am+n(m,n都是正整数)
文字描述:同底数幂相乘,底数不变,指数相加
推广: am·an·ap =am+n+p (m,n,p都是正整数)
例题讲解
例1 计算:
(1) ; (2) (-2)2×(-2)7 ;
(3) a2·a3·a6; (4) (-y)3· y4.
解:(1) ;
(2) (-2)2×(-2)7 =(-2)2+7=(-2)9 =-29 ;
(3) a2·a3·a6 =a2+3+6=a11;
(4) (-y)3· y4= -y3· y4= -y3+4 = -y7.
例2 计算:(1)a2·a3·a·a5;(2)(x-y)3·(y-x)5.
(2)(x-y)3·(y-x)5=(x-y)3·[-(x-y)5]
=-(x-y)3+5
=-(x-y)8.
解:(1) a2·a3·a·a5=a2+3+1+5=a11;
底数可以是一个单项式,也可以是一个多项式;
在幂的运算中常用到下面两种变形:
②(a-b)n=
①(-a)n=
an(n为偶数)
-an(n为奇数)
(b-a)n(n为偶数)
-(b-a)n(n为奇数)
例3 已知2x=5,求2x+2的值.
分析:根据同底数幂的乘法法则,am an=am+n(m,n为正整数),反之,am+n= am an,即逆用法则求值.
解:2x+2=2x 22=5×4 =20.
幂的各种运算的逆用将在后续的学习中频繁的出现,注意哦!
随堂演练
1. 下列各式中是同底数幂的是( )
A.23与32
B.a3与(-a)3
C.(m-n)5与(m-n)6
D.(a-b)2与(b-a)3
C
2. a16可以写成( )
A.a2·a8 B.a8+a8
C.a4·a8 D.a8·a8
D
3.下列各式中,计算正确的是( )
A.m2·m4=m6 B.m2·m4=m8
C.m2+m4=m6 D.m4·m4=2m8
A
4. 若a·a3·am=a8,则m=____.
4
5. 按一定规律排列的一列数:21,22,23,25,28,213,…,若x,y,z表示这列数中的连续三个数,猜想x,y,z满足的关系式是______.
xy=z
6. 计算:
(1)52×57; (2)7×73×72;
(3) -x2 x3; (4)(-c)3 (-c)m .
解:(1)52×57=52+7=59.
(2)7×73×72=71+3+2=76.
(3) -x2 x3=-x2+3=-x5.
(4)(-c)3 (-c)m =(-c)3+m.
7.(1)已知an-3·a2n+1=a10恒成立,求n的值;
(2)已知xa=2,xb=3,求xa+b的值.
解:(1)n-3+2n+1=10,
n=4;
(2)xa+b=xa·xb=2×3=6.
课堂小结
同底数幂的乘法
法则
am·an=am+n (m,n都是正整数)
注意
同底数幂相乘,底数不变,指数相加
am·an·ap=am+n+p(m,n,p都是正整数)
直接应用法则或逆用
底数相同时
底数不相同时
先变成同底数,
再应用法则或逆用
第8章 整式乘法与因式分解
8.1 第1课时 同底数幂的乘法
知识回顾
求几个相同因数的积的运算.
1. 乘方:
2. 幂:
乘方的结果.
指数
a的n次幂
获取新知
问题 我国首台千万亿次超级计算机系统“天河一号” 计算机每秒可进行2.57×1015次运算,问它工作1 h (3.6×103 s)可进行多少次运算?
2.57×1015× 3.6×103
=2.57× 3.6×1015×103
=?
解决这个问题需要研究同底数幂的乘法.
观察上表,发现同底数幂相乘有什么规律
算式 运算过程 结果
22×23 2×2×2×2×2 25
103×104
a2 a3
a4 a5
怎样计算,am an
先完成下表:
10×10×10×10×10×10×10
a·a·a·a·a
a·a·a·a·a·a·a·a·a
a5
a9
107
总结归纳
am an = (a a … a) (a a … a)
=a a … a
=am+n
m 个 a
n 个 a
(m+n)个 a
符号表示:am an =am+n(m,n都是正整数)
文字描述:同底数幂相乘,底数不变,指数相加
推广: am·an·ap =am+n+p (m,n,p都是正整数)
例题讲解
例1 计算:
(1) ; (2) (-2)2×(-2)7 ;
(3) a2·a3·a6; (4) (-y)3· y4.
解:(1) ;
(2) (-2)2×(-2)7 =(-2)2+7=(-2)9 =-29 ;
(3) a2·a3·a6 =a2+3+6=a11;
(4) (-y)3· y4= -y3· y4= -y3+4 = -y7.
例2 计算:(1)a2·a3·a·a5;(2)(x-y)3·(y-x)5.
(2)(x-y)3·(y-x)5=(x-y)3·[-(x-y)5]
=-(x-y)3+5
=-(x-y)8.
解:(1) a2·a3·a·a5=a2+3+1+5=a11;
底数可以是一个单项式,也可以是一个多项式;
在幂的运算中常用到下面两种变形:
②(a-b)n=
①(-a)n=
an(n为偶数)
-an(n为奇数)
(b-a)n(n为偶数)
-(b-a)n(n为奇数)
例3 已知2x=5,求2x+2的值.
分析:根据同底数幂的乘法法则,am an=am+n(m,n为正整数),反之,am+n= am an,即逆用法则求值.
解:2x+2=2x 22=5×4 =20.
幂的各种运算的逆用将在后续的学习中频繁的出现,注意哦!
随堂演练
1. 下列各式中是同底数幂的是( )
A.23与32
B.a3与(-a)3
C.(m-n)5与(m-n)6
D.(a-b)2与(b-a)3
C
2. a16可以写成( )
A.a2·a8 B.a8+a8
C.a4·a8 D.a8·a8
D
3.下列各式中,计算正确的是( )
A.m2·m4=m6 B.m2·m4=m8
C.m2+m4=m6 D.m4·m4=2m8
A
4. 若a·a3·am=a8,则m=____.
4
5. 按一定规律排列的一列数:21,22,23,25,28,213,…,若x,y,z表示这列数中的连续三个数,猜想x,y,z满足的关系式是______.
xy=z
6. 计算:
(1)52×57; (2)7×73×72;
(3) -x2 x3; (4)(-c)3 (-c)m .
解:(1)52×57=52+7=59.
(2)7×73×72=71+3+2=76.
(3) -x2 x3=-x2+3=-x5.
(4)(-c)3 (-c)m =(-c)3+m.
7.(1)已知an-3·a2n+1=a10恒成立,求n的值;
(2)已知xa=2,xb=3,求xa+b的值.
解:(1)n-3+2n+1=10,
n=4;
(2)xa+b=xa·xb=2×3=6.
课堂小结
同底数幂的乘法
法则
am·an=am+n (m,n都是正整数)
注意
同底数幂相乘,底数不变,指数相加
am·an·ap=am+n+p(m,n,p都是正整数)
直接应用法则或逆用
底数相同时
底数不相同时
先变成同底数,
再应用法则或逆用
