沪科版数学七年级下册同步课件:8.2.1 第2课时 单项式与单项式相除(共15张PPT)
文档属性
| 名称 | 沪科版数学七年级下册同步课件:8.2.1 第2课时 单项式与单项式相除(共15张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 235.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-02 08:44:47 | ||
图片预览




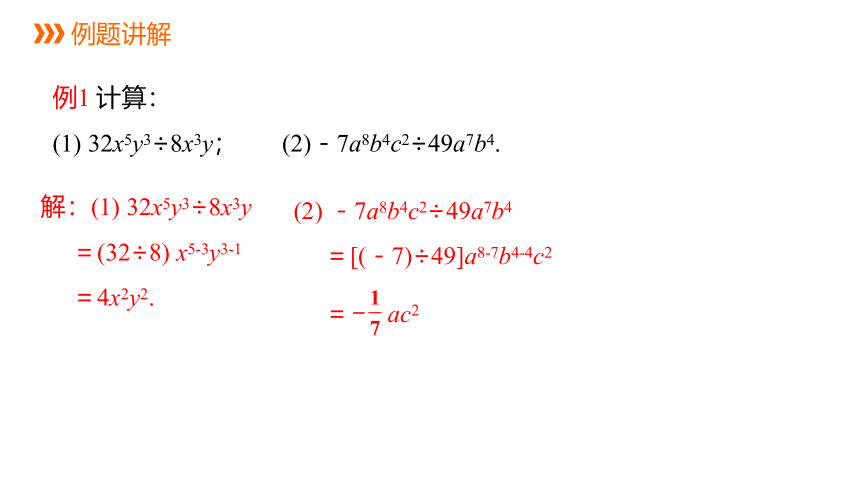

文档简介
(共15张PPT)
第8章 整式乘法与因式分解
8.2.1 第2课时 单项式与单项式相除
知识回顾
1.用字母表示幂的运算性质:
2.单项式乘单项式的运算法则:
单项式相乘,把系数、同底数幂分别相乘,作为积的因式;对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式 .
获取新知
怎样计算15a4b3x2÷3a2b3
我们知道,计算15a4b3x2÷3a2b3,就是要求一个单项式,使它与3a2b3相乘的积等于15a4b3x2 .
利用除法是乘法的逆运算来考虑
因为 (5a2x2) (3a2b3) = 15a4b3x2,
所以 15a4b3x2÷3a2b3 = 5a2x2 .
分析所得式子,能得到什么规律?
利用单项式与单项式相乘的法则就可以逆推出单项式与单项式相除的法则
单项式相除, 把系数、同底数幂分别相除作为商的因式;对于只在被除式中出现的字母,则连同它的指数一起作为商的一个因式.
单项式除以单项式的法则
归纳总结
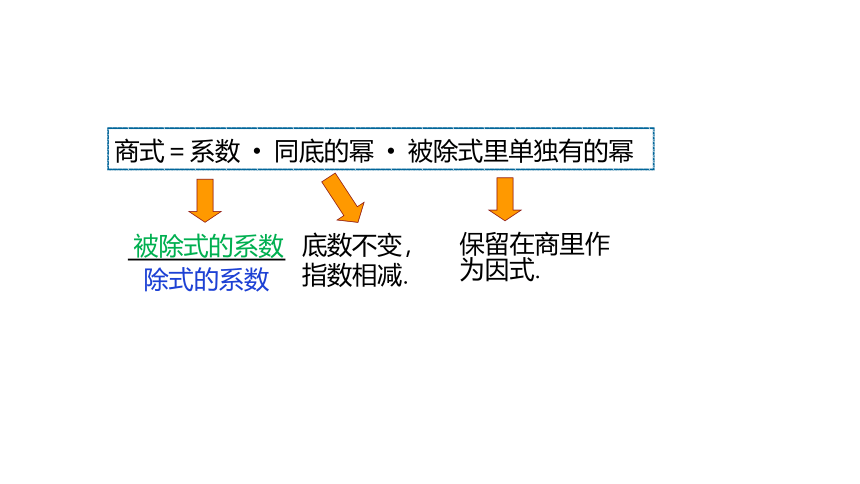
商式=系数 同底的幂 被除式里单独有的幂
底数不变,
指数相减.
保留在商里作为因式.
被除式的系数
除式的系数
例题讲解
例1 计算:
(1) 32x5y3÷8x3y; (2)-7a8b4c2÷49a7b4.
解:(1) 32x5y3÷8x3y
=(32÷8) x5-3y3-1
=4x2y2.
(2) -7a8b4c2÷49a7b4
=[(-7)÷49]a8-7b4-4c2
= ac2
例2 “卡西尼”号土星探测器历经7年多、行程约3.5×109 km后进入环绕土星运行的轨道.
(1)它的这一行程相当于地球赤道多少圈?(已知地球半
径6.4×103 km,π取 3.14 )
(2) 这一行程如果由速度是100 km/h的汽车来完成,
需要行驶多少年?(1年按365天计算)
(3) 这一行程如果由速度是10 m/s的短跑飞人来完成,
需要跑多少年?
解:(1) 3.5×109÷(2×3. 14×6.4×103) ≈ 8.7×104(圈).
探测器的行程相当于地球赤道约87 000圈.
(2) 3.5×109÷(365×24×100) ≈ 4.0×103(年).
探测器的行程相当于由速度为100 km/h的汽车行驶约4000 年.
(3) 3.5×109÷( 365×24×3.6×103×10×10-3) ≈ 1.1×104(年).探测器的行程相当于由速度为10 m/s的短跑飞人跑约11000 年.
随堂演练
1. 计算-4x3÷2x的结果正确的是( )
A.-2x2 B.2x2 C.-2x3 D.-8x4
A
2. 下列计算中,不正确的是( )
A.-2x+3x=x
B.6xy2÷2xy=3y
C.(-2x2y)3=-6x6y3
D.2xy2·(-x)=-2x2y2
C
3.已知28a3bm÷28anb2=b2,那么m,n的值分别为( )
A.4,3 B.4,1 C.1,3 D.2,3
A
4.计算:-4x5÷2x3=[(-4)÷ ]·( ÷ )= .
2
x5
x3
-2x2
5.计算:(a+1)3÷(a+1)2= .
a+1
6. 计算:
2a6b3÷a3b2; (2) ;
(3) 3m2n3÷(mn) 2;(4) (2x2y)3÷6x3y2 .
解:(1)2a6b3÷a3b2=2a6-3b3-2=2a3b.
(3)3m2n3÷(mn)2=3m2n3÷m2n2=3m2-2n3-2=3n.
(4)(2x2y)3÷6x3y2=8x6y3÷6x3y2=(8÷6)x6-3y3-2
7. 下雨时,常常是“先见闪电、后闻雷鸣”,这是因为光速比声速快的缘故.已知光在空气中的传播速度为3.0×108米/秒,而声音在空气中的传播速度约300米/秒,你知道光速是声速的多少倍吗?
解:3×108÷300
=3×108÷(3×102)
=106
=1000000
答:光速大约是声速的1000000倍,即100万倍.
课堂小结
单项式÷
单项式
运算法则
1.系数相除;
2.同底数的幂相除;
3.只在被除式里出现的因式照搬作为商的一个因式
注意
1.不要遗漏只在被除式中有而除式中没有的字母及字母的指数;
2.系数相除时,应连同它前面的符号一起进行运算.
第8章 整式乘法与因式分解
8.2.1 第2课时 单项式与单项式相除
知识回顾
1.用字母表示幂的运算性质:
2.单项式乘单项式的运算法则:
单项式相乘,把系数、同底数幂分别相乘,作为积的因式;对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式 .
获取新知
怎样计算15a4b3x2÷3a2b3
我们知道,计算15a4b3x2÷3a2b3,就是要求一个单项式,使它与3a2b3相乘的积等于15a4b3x2 .
利用除法是乘法的逆运算来考虑
因为 (5a2x2) (3a2b3) = 15a4b3x2,
所以 15a4b3x2÷3a2b3 = 5a2x2 .
分析所得式子,能得到什么规律?
利用单项式与单项式相乘的法则就可以逆推出单项式与单项式相除的法则
单项式相除, 把系数、同底数幂分别相除作为商的因式;对于只在被除式中出现的字母,则连同它的指数一起作为商的一个因式.
单项式除以单项式的法则
归纳总结
商式=系数 同底的幂 被除式里单独有的幂
底数不变,
指数相减.
保留在商里作为因式.
被除式的系数
除式的系数
例题讲解
例1 计算:
(1) 32x5y3÷8x3y; (2)-7a8b4c2÷49a7b4.
解:(1) 32x5y3÷8x3y
=(32÷8) x5-3y3-1
=4x2y2.
(2) -7a8b4c2÷49a7b4
=[(-7)÷49]a8-7b4-4c2
= ac2
例2 “卡西尼”号土星探测器历经7年多、行程约3.5×109 km后进入环绕土星运行的轨道.
(1)它的这一行程相当于地球赤道多少圈?(已知地球半
径6.4×103 km,π取 3.14 )
(2) 这一行程如果由速度是100 km/h的汽车来完成,
需要行驶多少年?(1年按365天计算)
(3) 这一行程如果由速度是10 m/s的短跑飞人来完成,
需要跑多少年?
解:(1) 3.5×109÷(2×3. 14×6.4×103) ≈ 8.7×104(圈).
探测器的行程相当于地球赤道约87 000圈.
(2) 3.5×109÷(365×24×100) ≈ 4.0×103(年).
探测器的行程相当于由速度为100 km/h的汽车行驶约4000 年.
(3) 3.5×109÷( 365×24×3.6×103×10×10-3) ≈ 1.1×104(年).探测器的行程相当于由速度为10 m/s的短跑飞人跑约11000 年.
随堂演练
1. 计算-4x3÷2x的结果正确的是( )
A.-2x2 B.2x2 C.-2x3 D.-8x4
A
2. 下列计算中,不正确的是( )
A.-2x+3x=x
B.6xy2÷2xy=3y
C.(-2x2y)3=-6x6y3
D.2xy2·(-x)=-2x2y2
C
3.已知28a3bm÷28anb2=b2,那么m,n的值分别为( )
A.4,3 B.4,1 C.1,3 D.2,3
A
4.计算:-4x5÷2x3=[(-4)÷ ]·( ÷ )= .
2
x5
x3
-2x2
5.计算:(a+1)3÷(a+1)2= .
a+1
6. 计算:
2a6b3÷a3b2; (2) ;
(3) 3m2n3÷(mn) 2;(4) (2x2y)3÷6x3y2 .
解:(1)2a6b3÷a3b2=2a6-3b3-2=2a3b.
(3)3m2n3÷(mn)2=3m2n3÷m2n2=3m2-2n3-2=3n.
(4)(2x2y)3÷6x3y2=8x6y3÷6x3y2=(8÷6)x6-3y3-2
7. 下雨时,常常是“先见闪电、后闻雷鸣”,这是因为光速比声速快的缘故.已知光在空气中的传播速度为3.0×108米/秒,而声音在空气中的传播速度约300米/秒,你知道光速是声速的多少倍吗?
解:3×108÷300
=3×108÷(3×102)
=106
=1000000
答:光速大约是声速的1000000倍,即100万倍.
课堂小结
单项式÷
单项式
运算法则
1.系数相除;
2.同底数的幂相除;
3.只在被除式里出现的因式照搬作为商的一个因式
注意
1.不要遗漏只在被除式中有而除式中没有的字母及字母的指数;
2.系数相除时,应连同它前面的符号一起进行运算.
