北师大版数学七年级下册 2.3.2平行线的性质(平行线的性质与判定的综合应用)-课件
文档属性
| 名称 | 北师大版数学七年级下册 2.3.2平行线的性质(平行线的性质与判定的综合应用)-课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 258.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-30 17:36:27 | ||
图片预览



文档简介
(共15张PPT)
第二章 平行线与相交线
2.3 平行线的性质
回顾与思考
问题1: 平行线的性质有哪几条?
问题2:判别直线平行的条件有哪几个?
你现在一共有几个判定直线平行的方法?
问题3:在应用二者时应注意什么问题?
目标检测1
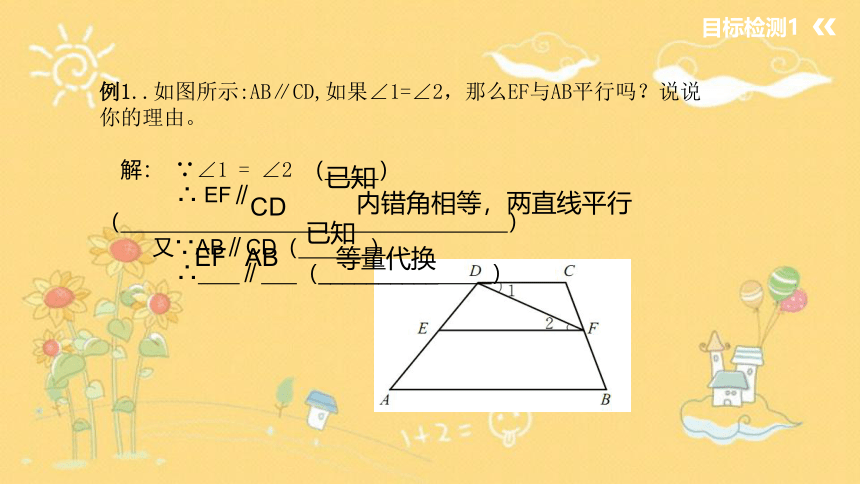
例1..如图所示:AB∥CD,如果∠1=∠2,那么EF与AB平行吗?说说你的理由。
解: ∵∠1 = ∠2 ( )
∴ EF∥ ( )
又∵AB∥CD( )
∴ ∥ (__________ )
已知
CD
AB
EF
已知
内错角相等,两直线平行
等量代换
目标检测1
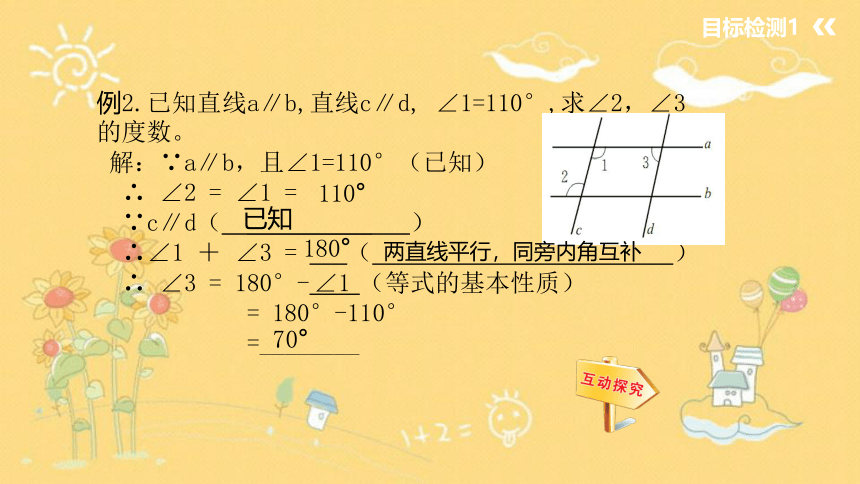
例2.已知直线a∥b,直线c∥d, ∠1=110°,求∠2,∠3的度数。
解:∵a∥b,且∠1=110°(已知)
∴ ∠2 = ∠1 =
∵c∥d( __________ )
∴∠1 + ∠3 = ( )
∴ ∠3 = 180°- (等式的基本性质)
= 180°-110°
=________
110°
已知
180°
两直线平行,同旁内角互补
∠1
70°
规律总结
平行线的性质与判定的区别与联系
1.区别:(1)性质:根据两条直线平行,证角的相等或互补.
(2)判定:根据两角相等或互补,证两条直线平行.
2.联系:它们都是以两条直线被第三条直线所截为前提;它们的条件和结论是互逆的.
3.总结:已知平行用性质,要证平行用判定.
目标检测2
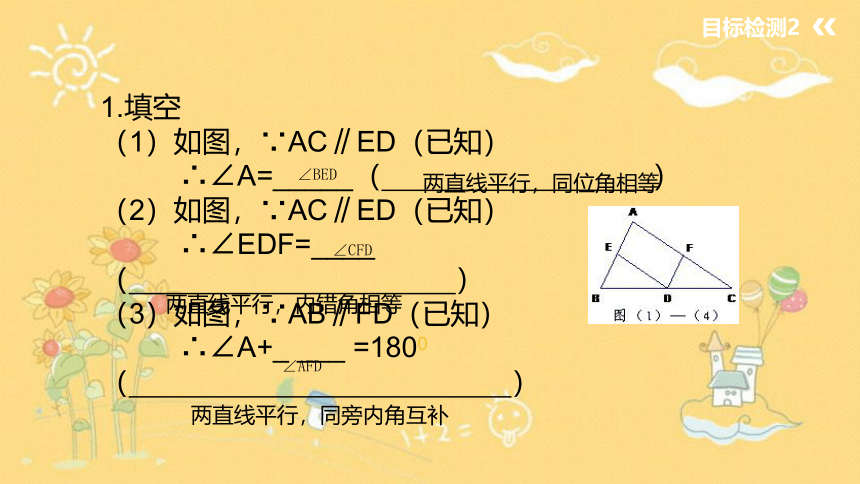
1.填空
(1)如图,∵AC∥ED(已知)
∴∠A=_____( )
(2)如图,∵AC∥ED(已知)
∴∠EDF=____
( )
(3)如图,∵AB∥FD(已知)
∴∠A+_ ___ =1800
( )
∠BED
两直线平行,同位角相等
∠CFD
两直线平行,内错角相等
∠AFD
两直线平行,同旁内角互补
目标检测2
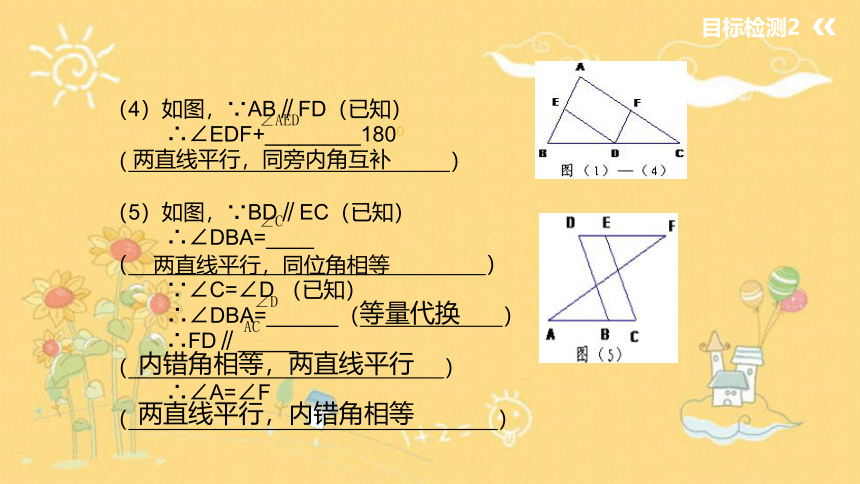
(4)如图,∵AB∥FD(已知)
∴∠EDF+________1800
( )
(5)如图,∵BD∥EC(已知)
∴∠DBA=____
( )
∵∠C=∠D (已知)
∴∠DBA=______( )
∴FD∥_____
( )
∴∠A=∠F ( )
∠AED
两直线平行,同旁内角互补
AC
两直线平行,同位角相等
∠D
等量代换
内错角相等,两直线平行
两直线平行,内错角相等
∠C
拓展提升
4.已知,如图,∠1=∠ACB,∠2=∠3,
FH⊥AB于H.问CD与AB有什么关系?
目标检测3
1.(衡阳中考)如图,直线a⊥直线c,
直线b⊥直线c,若∠1=70°,则∠2=( )
(A)70° (B)90°
(C)110° (D)80°
【解析】选A.因为a⊥c,b⊥c,所以a∥b.
所以∠1=∠3. 因为∠2=∠3,∠1=70°.
所以∠2=∠1=70°.
目标检测3
2.如图, 已知直线AB∥CD,∠C=115°,
∠A=25°,则∠E=( )
(A)70° (B)80°
(C)90° (D)100°
【解析】选C.因为AB∥CD,
所以∠EFB=∠C=115°,
因为∠EFB+∠AFE=180°,所以∠AFE=65°,
因为∠A+∠E+∠AFE=180°,∠A=25°,
所以∠E=90°.
拓展
1.如图,一条公路两次拐弯前后两条路互相平行.第一次拐的角∠B是142゜,第二次 拐的角∠C是多少度?为什么?
B
C
解:∠C=142o
∵两直线平行,内错角相等
课堂小结
1、本节课主要应用了哪些知识?
2、在应用它们时,你认为应该注意哪些问题?
3、在写几何推理的过程中,因为和所以分
别表达的意义是什么?根据是什么?
限时检测(5分钟)
A
限时检测(5分钟)
B
作业布置
1、完成导学案剩余练习
2、完成数学作业本相应练习
3、完成训练案相应练习
第二章 平行线与相交线
2.3 平行线的性质
回顾与思考
问题1: 平行线的性质有哪几条?
问题2:判别直线平行的条件有哪几个?
你现在一共有几个判定直线平行的方法?
问题3:在应用二者时应注意什么问题?
目标检测1
例1..如图所示:AB∥CD,如果∠1=∠2,那么EF与AB平行吗?说说你的理由。
解: ∵∠1 = ∠2 ( )
∴ EF∥ ( )
又∵AB∥CD( )
∴ ∥ (__________ )
已知
CD
AB
EF
已知
内错角相等,两直线平行
等量代换
目标检测1
例2.已知直线a∥b,直线c∥d, ∠1=110°,求∠2,∠3的度数。
解:∵a∥b,且∠1=110°(已知)
∴ ∠2 = ∠1 =
∵c∥d( __________ )
∴∠1 + ∠3 = ( )
∴ ∠3 = 180°- (等式的基本性质)
= 180°-110°
=________
110°
已知
180°
两直线平行,同旁内角互补
∠1
70°
规律总结
平行线的性质与判定的区别与联系
1.区别:(1)性质:根据两条直线平行,证角的相等或互补.
(2)判定:根据两角相等或互补,证两条直线平行.
2.联系:它们都是以两条直线被第三条直线所截为前提;它们的条件和结论是互逆的.
3.总结:已知平行用性质,要证平行用判定.
目标检测2
1.填空
(1)如图,∵AC∥ED(已知)
∴∠A=_____( )
(2)如图,∵AC∥ED(已知)
∴∠EDF=____
( )
(3)如图,∵AB∥FD(已知)
∴∠A+_ ___ =1800
( )
∠BED
两直线平行,同位角相等
∠CFD
两直线平行,内错角相等
∠AFD
两直线平行,同旁内角互补
目标检测2
(4)如图,∵AB∥FD(已知)
∴∠EDF+________1800
( )
(5)如图,∵BD∥EC(已知)
∴∠DBA=____
( )
∵∠C=∠D (已知)
∴∠DBA=______( )
∴FD∥_____
( )
∴∠A=∠F ( )
∠AED
两直线平行,同旁内角互补
AC
两直线平行,同位角相等
∠D
等量代换
内错角相等,两直线平行
两直线平行,内错角相等
∠C
拓展提升
4.已知,如图,∠1=∠ACB,∠2=∠3,
FH⊥AB于H.问CD与AB有什么关系?
目标检测3
1.(衡阳中考)如图,直线a⊥直线c,
直线b⊥直线c,若∠1=70°,则∠2=( )
(A)70° (B)90°
(C)110° (D)80°
【解析】选A.因为a⊥c,b⊥c,所以a∥b.
所以∠1=∠3. 因为∠2=∠3,∠1=70°.
所以∠2=∠1=70°.
目标检测3
2.如图, 已知直线AB∥CD,∠C=115°,
∠A=25°,则∠E=( )
(A)70° (B)80°
(C)90° (D)100°
【解析】选C.因为AB∥CD,
所以∠EFB=∠C=115°,
因为∠EFB+∠AFE=180°,所以∠AFE=65°,
因为∠A+∠E+∠AFE=180°,∠A=25°,
所以∠E=90°.
拓展
1.如图,一条公路两次拐弯前后两条路互相平行.第一次拐的角∠B是142゜,第二次 拐的角∠C是多少度?为什么?
B
C
解:∠C=142o
∵两直线平行,内错角相等
课堂小结
1、本节课主要应用了哪些知识?
2、在应用它们时,你认为应该注意哪些问题?
3、在写几何推理的过程中,因为和所以分
别表达的意义是什么?根据是什么?
限时检测(5分钟)
A
限时检测(5分钟)
B
作业布置
1、完成导学案剩余练习
2、完成数学作业本相应练习
3、完成训练案相应练习
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
