沪科版数学七年级下册 9.3 分式方程(5) 课件
文档属性
| 名称 | 沪科版数学七年级下册 9.3 分式方程(5) 课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 187.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-30 17:46:14 | ||
图片预览






文档简介
(共15张PPT)
9.3 分式方程
复习巩固
1、什么是方程?
2、什么是分式?
3、最简公分母是怎样找到的?
含有未知数的等式。
分母中含有字母的式子
1)系数:最小公倍数
2)相同因式:最高次幂
3)不同因式:连同其指数
思考
洪老师从家到学校,步行走了1千米,骑车行驶了6千米,其中骑车比步行的速度快25千米/时,骑车和步行所用的时间相同,求洪老师步行的速度为 多少千米/时?
解:设洪老师步行的速度为x千米/时,则洪老师骑车的速度为 千米/时,步行所用的时间
为 小时,洪老师骑车所用的时间为 小时,由题意可列式:
分式方程的定义
像这样,分母里含有未知数的方程叫做分式方程。
以前学过的分母里不含有未知数的方程叫做整式方程。
1.判断下列说法是否正确:
(×)
(√ )
( √)
( √)
小试牛刀
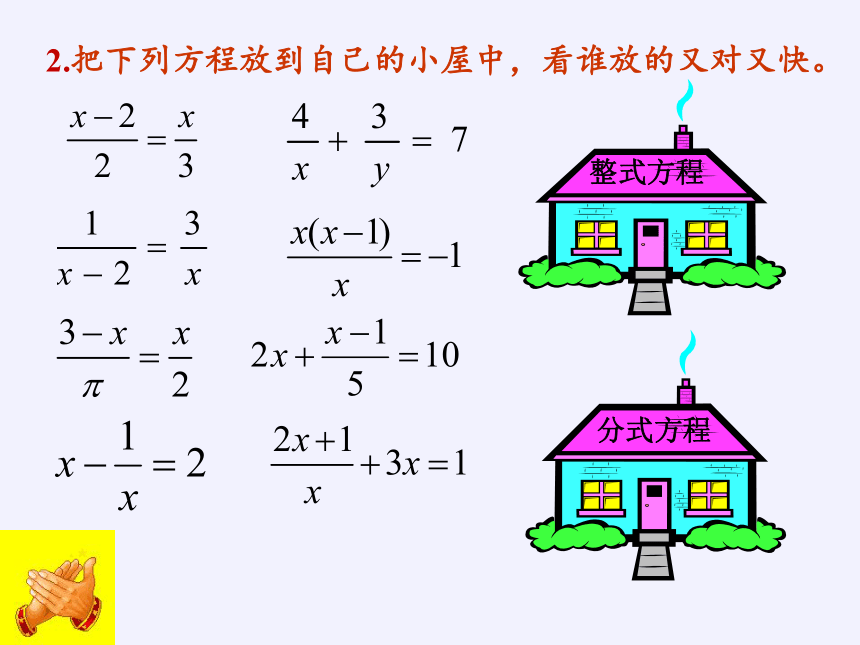
2.把下列方程放到自己的小屋中,看谁放的又对又快。
整式方程
分式方程
2.把下列方程放到自己的小屋中,看谁放的又对又快。
区别
分式方程的分母中含有未知数;
整式方程的分母中不含有未知数。
解:
在方程两边都乘以最简公分母(x+25)x得,
解这个整式方程得: x=5
检验:把x= 5 代入原方程中,左边=右边
∴ x=5是原方程的解
探究
下面我们一起研究下怎么样来解分式方程:
【解分式方程】
1
x-5
10
=
x2-25
解:
解这个整式方程,得x=5
x+5=10
检验:把x = 5 代入原方程中,方程中分式的分母的值都为0,相应的分式无意义,因此x=5虽是方程x+5=10的解,但不是原分式方程的解.实际上,这个分式方程无解。
我们把这个使方程无意义的根叫增根!
1
x-5
10
=
x2-25
×(x+5)(x-5)
×(x+5)(x-5)
解分式方程的思路是:
分式方程
整式方程
去分母
增根
是整式方程的根
不是分式方程的根
解下列分式方程
(1)
(2)
课堂小试
解分式方程的一般步骤
1、方程的两边都乘以最简公分母,约去分母,化成整式方程.
2、解这个整式方程.
3、把整式方程的解代入最简公分母检验,如果最简公分母的值不为0,则整式方程的解是原分式方程的解;否则,这个解不是原分式方程的解,必须舍去.并写出原方程的根
一化二解三检验
小 结
本节课你有什么收获?
1、解分式方程的一般步骤?
2、解分式方程最后应注意什么?
一化二解三检验
验根
课堂作业:P109第3题(2)、(4)
再见!
谢 谢
9.3 分式方程
复习巩固
1、什么是方程?
2、什么是分式?
3、最简公分母是怎样找到的?
含有未知数的等式。
分母中含有字母的式子
1)系数:最小公倍数
2)相同因式:最高次幂
3)不同因式:连同其指数
思考
洪老师从家到学校,步行走了1千米,骑车行驶了6千米,其中骑车比步行的速度快25千米/时,骑车和步行所用的时间相同,求洪老师步行的速度为 多少千米/时?
解:设洪老师步行的速度为x千米/时,则洪老师骑车的速度为 千米/时,步行所用的时间
为 小时,洪老师骑车所用的时间为 小时,由题意可列式:
分式方程的定义
像这样,分母里含有未知数的方程叫做分式方程。
以前学过的分母里不含有未知数的方程叫做整式方程。
1.判断下列说法是否正确:
(×)
(√ )
( √)
( √)
小试牛刀
2.把下列方程放到自己的小屋中,看谁放的又对又快。
整式方程
分式方程
2.把下列方程放到自己的小屋中,看谁放的又对又快。
区别
分式方程的分母中含有未知数;
整式方程的分母中不含有未知数。
解:
在方程两边都乘以最简公分母(x+25)x得,
解这个整式方程得: x=5
检验:把x= 5 代入原方程中,左边=右边
∴ x=5是原方程的解
探究
下面我们一起研究下怎么样来解分式方程:
【解分式方程】
1
x-5
10
=
x2-25
解:
解这个整式方程,得x=5
x+5=10
检验:把x = 5 代入原方程中,方程中分式的分母的值都为0,相应的分式无意义,因此x=5虽是方程x+5=10的解,但不是原分式方程的解.实际上,这个分式方程无解。
我们把这个使方程无意义的根叫增根!
1
x-5
10
=
x2-25
×(x+5)(x-5)
×(x+5)(x-5)
解分式方程的思路是:
分式方程
整式方程
去分母
增根
是整式方程的根
不是分式方程的根
解下列分式方程
(1)
(2)
课堂小试
解分式方程的一般步骤
1、方程的两边都乘以最简公分母,约去分母,化成整式方程.
2、解这个整式方程.
3、把整式方程的解代入最简公分母检验,如果最简公分母的值不为0,则整式方程的解是原分式方程的解;否则,这个解不是原分式方程的解,必须舍去.并写出原方程的根
一化二解三检验
小 结
本节课你有什么收获?
1、解分式方程的一般步骤?
2、解分式方程最后应注意什么?
一化二解三检验
验根
课堂作业:P109第3题(2)、(4)
再见!
谢 谢
