沪科版数学八年级下册同步课时练习:第18章 勾股定理 自我综合评价
文档属性
| 名称 | 沪科版数学八年级下册同步课时练习:第18章 勾股定理 自我综合评价 |

|
|
| 格式 | docx | ||
| 文件大小 | 169.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-02 11:26:58 | ||
图片预览


文档简介
数学
化学
第18章 勾股定理
一、选择题(本大题共6小题,每小题5分,共30分)
1.在Rt△ABC中,∠C=90°,a,b,c分别是∠A,∠B,∠C的对边,下列式子中,不正确的是 ( )
A.a2+b2=c2 B.c2-a2=b2
C.a= D.a2-b2=c2
2.(2020合肥包河区期末)在△ABC中,三边长分别为a,b,c,且a+c=2b,c-a=b,则△ABC是 ( )
A.直角三角形 B.等边三角形
C.等腰三角形 D.等腰直角三角形
3.在Rt△ABC中,斜边BC=2,则AB2+AC2+BC2的值为 ( )
A.8 B.4
C.6 D.无法计算
4.如图1,直线l上有三个正方形a,b,c,若a,c的面积分别为5和11,则b的面积为 ( )
图1
A.4 B.6 C.16 D.55
5.小明家门框的尺寸如图1所示,为装修房子买了一种“三合板”,若从进门方便的角度考虑,则可选的尺寸为 ( )
图1
A.长为4 m,宽为2.5 m B.长为8 m,宽为2.1 m
C.长为3 m,宽为2.9 m D.以上均不合适
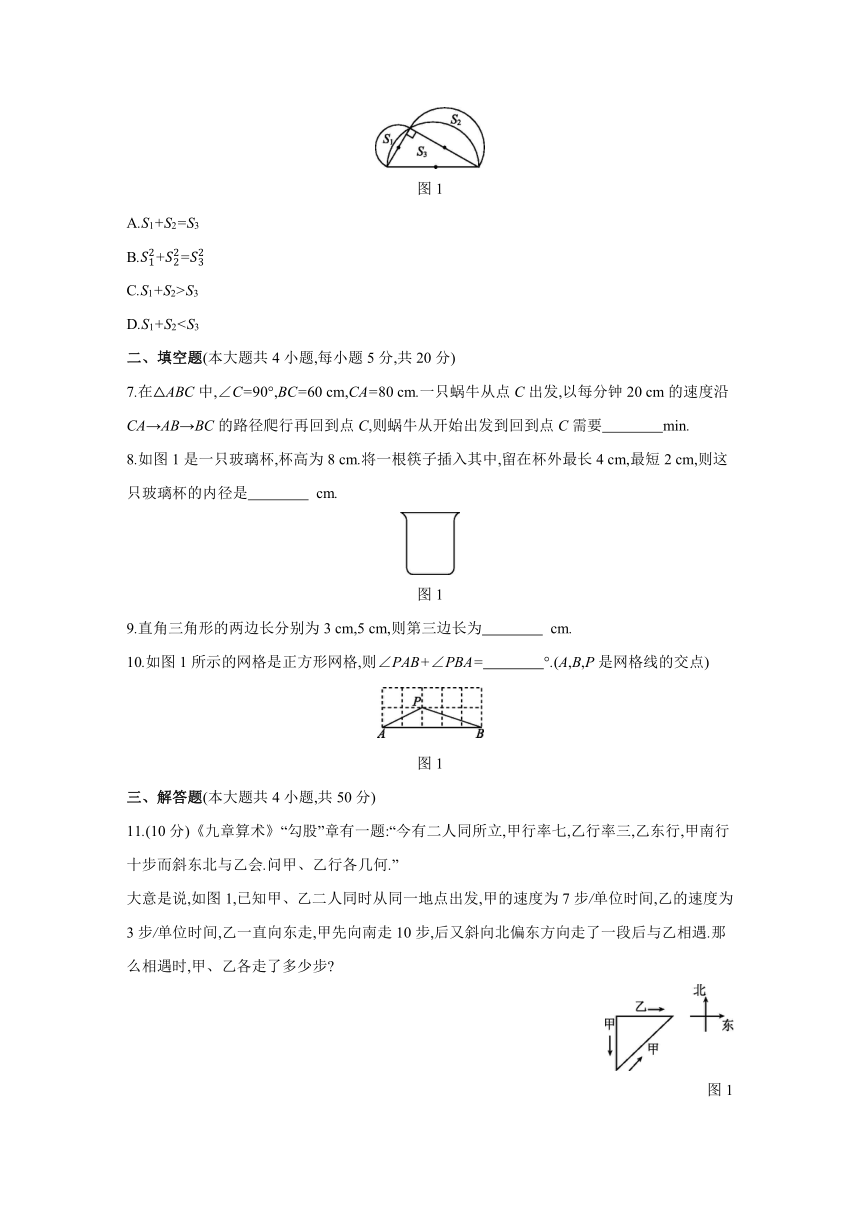
6.如图1所示,以直角三角形的三边为直径的半圆的面积从小到大依次记为S1,S2,S3,则S1,S2,S3的关系是 ( )
图1
A.S1+S2=S3
B.+=
C.S1+S2>S3
D.S1+S2二、填空题(本大题共4小题,每小题5分,共20分)
7.在△ABC中,∠C=90°,BC=60 cm,CA=80 cm.一只蜗牛从点C出发,以每分钟20 cm的速度沿CA→AB→BC的路径爬行再回到点C,则蜗牛从开始出发到回到点C需要 min.
8.如图1是一只玻璃杯,杯高为8 cm.将一根筷子插入其中,留在杯外最长4 cm,最短2 cm,则这只玻璃杯的内径是 cm.
图1
9.直角三角形的两边长分别为3 cm,5 cm,则第三边长为 cm.
10.如图1所示的网格是正方形网格,则∠PAB+∠PBA= °.(A,B,P是网格线的交点)
图1
三、解答题(本大题共4小题,共50分)
11.(10分)《九章算术》“勾股”章有一题:“今有二人同所立,甲行率七,乙行率三,乙东行,甲南行十步而斜东北与乙会.问甲、乙行各几何.”
大意是说,如图1,已知甲、乙二人同时从同一地点出发,甲的速度为7步/单位时间,乙的速度为3步/单位时间,乙一直向东走,甲先向南走10步,后又斜向北偏东方向走了一段后与乙相遇.那么相遇时,甲、乙各走了多少步
图1
12.(12分)如图1,在甲村到乙村的公路旁有一块山地正在开发,现有C处需要爆破.已知点C与公路上的停靠站A,B的距离分别为300 m和400 m,且AC⊥BC,为了安全起见,如果爆破点C周围半径250 m的区域内不能有车辆和行人,问在进行爆破时,公路AB段是否需要暂时封闭,为什么
图1
13.(14分)如图1是一张放在平面直角坐标系中的长方形纸片OABC,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8,在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,求D,E两点的坐标.
图1
14.(14分)如图1,在Rt△ABC中,∠ACB=90°,AB=5 cm,AC=3 cm.动点P从点B出发沿射线BC以2 cm/s的速度运动,设运动的时间为t s.
(1)当△ABP为直角三角形时,求t的值;
(2)当△ABP为等腰三角形时,求t的值.
图1
答案
1.D 因为∠C=90°,所以斜边为c,而D选项中a2-b2=c2,a为斜边,所以D选项错误.
2.A ∵a+c=2b,c-a=b,∴c2-a2=b2,∴△ABC是直角三角形.
3.A ∵在Rt△ABC中,BC为斜边,
∴AB2+AC2=BC2,
∴AB2+AC2+BC2=2BC2=2×22=8.
4.C 如图,易知Rt△ABC≌Rt△DAE,则BC=AE,AC=DE.在Rt△ABC中,由勾股定理,得BC2+AC2=AB2,即b的面积=a的面积+c的面积=5+11=16.故选C.
5.B 根据勾股定理,得门框的对角线长为 m,约为2.2 m,所选的三合板尺寸中,长或宽中至少有一个小于2.2 m,才能运到屋内,因此,只有B项符合.故选B.
6.A 如图所示,设直角三角形各边长分别为2a,2b,2c.
∵三角形是直角三角形,
∴(2a)2+(2b)2=(2c)2,化简,得a2+b2=c2.
∵S1=πa2,S2=πb2,S3=πc2,
∴S1+S2=π(a2+b2)=πc2=S3.故选A.
7.12 由勾股定理可知AB===100(cm), △ABC的周长为60+80+100=240(cm),则240÷20=12(min),所以蜗牛从开始出发到回到点C需要12 min.
8.6
9.或4 ①当3 cm和5 cm都是直角边时,第三边为斜边,
由勾股定理,得第三边长为=(cm);
②当3 cm为直角边,5 cm为斜边时,第三边为直角边,
由勾股定理,得第三边长为=4(cm).
10.45 如图,延长AP至格点D,连接BD.
设小正方形的边长均为1,由图知PD2=BD2=12+22=5,PB2=12+32=10,
∴PD2+DB2=PB2,∴∠PDB=90°,
∴∠PAB+∠PBA=∠DPB=45°.
11.解:如图,设经过x个单位时间二人在B处相遇,这时乙共走了AB=3x步,甲共走了AC+BC=7x步.
∵AC=10,∴BC=7x-10.
又∵∠A=90°,∴BC2=AC2+AB2,
∴(7x-10)2=102+(3x)2,
解得x1=0(舍去),x2=3.5,
∴AB=3x=10.5,AC+BC=7x=24.5.
答:甲走了24.5步,乙走了10.5步.
12.解:公路AB段需要暂时封闭.
理由如下:如图,过点C作CD⊥AB于点D.
在Rt△ABC中,由勾股定理,得AB2=AC2+BC2=3002+4002=250000,
所以AB=500 m.
由S△ABC=AB·CD=AC·BC,
得500CD=300×400,
解得CD=240 m.
因为240<250,
所以在进行爆破时,公路AB段有危险,需要暂时封闭.
13.解:依题意可知,AE=OA=10,AB=OC=8,
∴在Rt△ABE中,BE===6,
∴CE=CB-BE=10-6=4,∴E(4,8).
由折叠的性质,得DE=OD,
在Rt△DCE中,DC2+CE2=DE2,
∴(8-OD)2+42=OD2,解得OD=5,
∴D(0,5).
综上,点D的坐标为(0,5),点E的坐标为(4,8).
14.解:(1)∵∠ACB=90°,AB=5 cm,AC=3 cm,
∴BC===4(cm).
①若∠APB为直角,则点P与点C重合,此时BP=BC=4 cm,
∴t=4÷2=2.
②若∠BAP为直角,则BP=2t cm,CP=(2t-4)cm.
在Rt△ACP中,AP2=32+(2t-4)2.
在Rt△BAP中,AB2+AP2=BP2,
∴52+[32+(2t-4)2]=(2t)2,
解得t=.
综上所述,当t的值为2或时,△ABP为直角三角形.
(2)①若BP=AB=5 cm,则t=.
②若AB=AP,则BP=2BC=8 cm,∴t=4.
③若BP=AP,则BP=AP=2t cm,CP=(4-2t) cm.
在Rt△ACP中,AP2=AC2+CP2,
∴(2t)2=32+(4-2t)2,解得t=.
综上所述,当t的值为或4或时,△ABP为等腰三角形.
化学
第18章 勾股定理
一、选择题(本大题共6小题,每小题5分,共30分)
1.在Rt△ABC中,∠C=90°,a,b,c分别是∠A,∠B,∠C的对边,下列式子中,不正确的是 ( )
A.a2+b2=c2 B.c2-a2=b2
C.a= D.a2-b2=c2
2.(2020合肥包河区期末)在△ABC中,三边长分别为a,b,c,且a+c=2b,c-a=b,则△ABC是 ( )
A.直角三角形 B.等边三角形
C.等腰三角形 D.等腰直角三角形
3.在Rt△ABC中,斜边BC=2,则AB2+AC2+BC2的值为 ( )
A.8 B.4
C.6 D.无法计算
4.如图1,直线l上有三个正方形a,b,c,若a,c的面积分别为5和11,则b的面积为 ( )
图1
A.4 B.6 C.16 D.55
5.小明家门框的尺寸如图1所示,为装修房子买了一种“三合板”,若从进门方便的角度考虑,则可选的尺寸为 ( )
图1
A.长为4 m,宽为2.5 m B.长为8 m,宽为2.1 m
C.长为3 m,宽为2.9 m D.以上均不合适
6.如图1所示,以直角三角形的三边为直径的半圆的面积从小到大依次记为S1,S2,S3,则S1,S2,S3的关系是 ( )
图1
A.S1+S2=S3
B.+=
C.S1+S2>S3
D.S1+S2
7.在△ABC中,∠C=90°,BC=60 cm,CA=80 cm.一只蜗牛从点C出发,以每分钟20 cm的速度沿CA→AB→BC的路径爬行再回到点C,则蜗牛从开始出发到回到点C需要 min.
8.如图1是一只玻璃杯,杯高为8 cm.将一根筷子插入其中,留在杯外最长4 cm,最短2 cm,则这只玻璃杯的内径是 cm.
图1
9.直角三角形的两边长分别为3 cm,5 cm,则第三边长为 cm.
10.如图1所示的网格是正方形网格,则∠PAB+∠PBA= °.(A,B,P是网格线的交点)
图1
三、解答题(本大题共4小题,共50分)
11.(10分)《九章算术》“勾股”章有一题:“今有二人同所立,甲行率七,乙行率三,乙东行,甲南行十步而斜东北与乙会.问甲、乙行各几何.”
大意是说,如图1,已知甲、乙二人同时从同一地点出发,甲的速度为7步/单位时间,乙的速度为3步/单位时间,乙一直向东走,甲先向南走10步,后又斜向北偏东方向走了一段后与乙相遇.那么相遇时,甲、乙各走了多少步
图1
12.(12分)如图1,在甲村到乙村的公路旁有一块山地正在开发,现有C处需要爆破.已知点C与公路上的停靠站A,B的距离分别为300 m和400 m,且AC⊥BC,为了安全起见,如果爆破点C周围半径250 m的区域内不能有车辆和行人,问在进行爆破时,公路AB段是否需要暂时封闭,为什么
图1
13.(14分)如图1是一张放在平面直角坐标系中的长方形纸片OABC,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8,在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,求D,E两点的坐标.
图1
14.(14分)如图1,在Rt△ABC中,∠ACB=90°,AB=5 cm,AC=3 cm.动点P从点B出发沿射线BC以2 cm/s的速度运动,设运动的时间为t s.
(1)当△ABP为直角三角形时,求t的值;
(2)当△ABP为等腰三角形时,求t的值.
图1
答案
1.D 因为∠C=90°,所以斜边为c,而D选项中a2-b2=c2,a为斜边,所以D选项错误.
2.A ∵a+c=2b,c-a=b,∴c2-a2=b2,∴△ABC是直角三角形.
3.A ∵在Rt△ABC中,BC为斜边,
∴AB2+AC2=BC2,
∴AB2+AC2+BC2=2BC2=2×22=8.
4.C 如图,易知Rt△ABC≌Rt△DAE,则BC=AE,AC=DE.在Rt△ABC中,由勾股定理,得BC2+AC2=AB2,即b的面积=a的面积+c的面积=5+11=16.故选C.
5.B 根据勾股定理,得门框的对角线长为 m,约为2.2 m,所选的三合板尺寸中,长或宽中至少有一个小于2.2 m,才能运到屋内,因此,只有B项符合.故选B.
6.A 如图所示,设直角三角形各边长分别为2a,2b,2c.
∵三角形是直角三角形,
∴(2a)2+(2b)2=(2c)2,化简,得a2+b2=c2.
∵S1=πa2,S2=πb2,S3=πc2,
∴S1+S2=π(a2+b2)=πc2=S3.故选A.
7.12 由勾股定理可知AB===100(cm), △ABC的周长为60+80+100=240(cm),则240÷20=12(min),所以蜗牛从开始出发到回到点C需要12 min.
8.6
9.或4 ①当3 cm和5 cm都是直角边时,第三边为斜边,
由勾股定理,得第三边长为=(cm);
②当3 cm为直角边,5 cm为斜边时,第三边为直角边,
由勾股定理,得第三边长为=4(cm).
10.45 如图,延长AP至格点D,连接BD.
设小正方形的边长均为1,由图知PD2=BD2=12+22=5,PB2=12+32=10,
∴PD2+DB2=PB2,∴∠PDB=90°,
∴∠PAB+∠PBA=∠DPB=45°.
11.解:如图,设经过x个单位时间二人在B处相遇,这时乙共走了AB=3x步,甲共走了AC+BC=7x步.
∵AC=10,∴BC=7x-10.
又∵∠A=90°,∴BC2=AC2+AB2,
∴(7x-10)2=102+(3x)2,
解得x1=0(舍去),x2=3.5,
∴AB=3x=10.5,AC+BC=7x=24.5.
答:甲走了24.5步,乙走了10.5步.
12.解:公路AB段需要暂时封闭.
理由如下:如图,过点C作CD⊥AB于点D.
在Rt△ABC中,由勾股定理,得AB2=AC2+BC2=3002+4002=250000,
所以AB=500 m.
由S△ABC=AB·CD=AC·BC,
得500CD=300×400,
解得CD=240 m.
因为240<250,
所以在进行爆破时,公路AB段有危险,需要暂时封闭.
13.解:依题意可知,AE=OA=10,AB=OC=8,
∴在Rt△ABE中,BE===6,
∴CE=CB-BE=10-6=4,∴E(4,8).
由折叠的性质,得DE=OD,
在Rt△DCE中,DC2+CE2=DE2,
∴(8-OD)2+42=OD2,解得OD=5,
∴D(0,5).
综上,点D的坐标为(0,5),点E的坐标为(4,8).
14.解:(1)∵∠ACB=90°,AB=5 cm,AC=3 cm,
∴BC===4(cm).
①若∠APB为直角,则点P与点C重合,此时BP=BC=4 cm,
∴t=4÷2=2.
②若∠BAP为直角,则BP=2t cm,CP=(2t-4)cm.
在Rt△ACP中,AP2=32+(2t-4)2.
在Rt△BAP中,AB2+AP2=BP2,
∴52+[32+(2t-4)2]=(2t)2,
解得t=.
综上所述,当t的值为2或时,△ABP为直角三角形.
(2)①若BP=AB=5 cm,则t=.
②若AB=AP,则BP=2BC=8 cm,∴t=4.
③若BP=AP,则BP=AP=2t cm,CP=(4-2t) cm.
在Rt△ACP中,AP2=AC2+CP2,
∴(2t)2=32+(4-2t)2,解得t=.
综上所述,当t的值为或4或时,△ABP为等腰三角形.
