沪科版数学八年级下册同步课件:16.2.2 第1课时 二次根式的加减
文档属性
| 名称 | 沪科版数学八年级下册同步课件:16.2.2 第1课时 二次根式的加减 |

|
|
| 格式 | pptx | ||
| 文件大小 | 247.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-02 12:12:04 | ||
图片预览





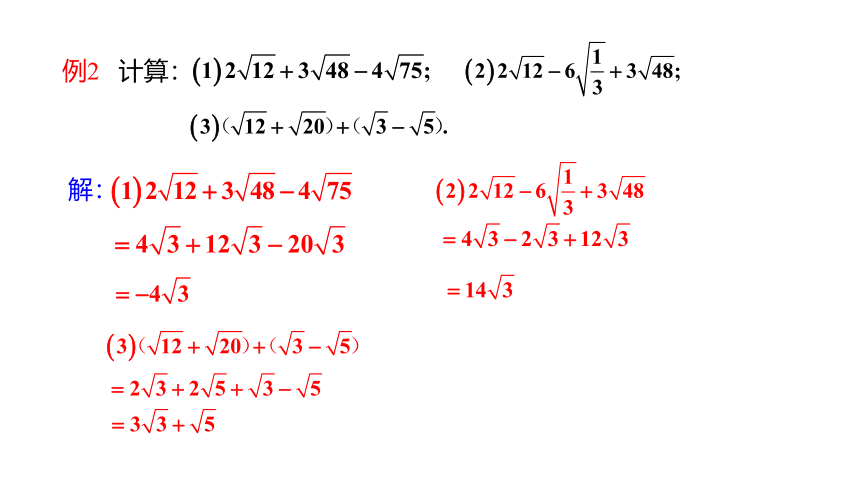

文档简介
(共14张PPT)
第16章 二次根式
16.2.2 第1课时 二次根式的加减
知识回顾
问题1 满足什么条件的根式是最简二次根式
(1)被开方数不含分母;
(2)被开方数中不含能开得尽方的因数或因式.
问题2 化简下列两组二次根式,每组化简后有什么共同特点
化简后被开方数相同
获取新知
如何进行二次根式的加减呢?
计算:
(化成最简二次根式)
(逆用乘法分配律)
同类二次根式:几个二次根式化成最简二次根式后,如果它们的被开方数相同,像这样的二次根式称为同类二次根式.
归纳总结
二次根式的加减法法则:
一般地,二次根式相加减,先把各个二次根式化成最简二次根式,再把同类二次根式进行合并.
(1)化——将非最简二次根式的二次根式化简;
二次根式加减法的运算步骤:
(2)找——找出同类二次根式;
(3)并——把同类二次根式的系数相加减,其他的不变.
即:
例题讲解
例1 下列根式中,不能与 合并的是( )
A. B. C. D.
C
导引:首先把选项中每个根式化成最简二次根式,然后找出被开方数不是3的二次根式.即
解:
例2 计算:
二次根式加减运算的技巧:
(1)将每个二次根式都化为最简二次根式,若被开方数中含有带分数,则要先化成假分数;若含有小数,则要化成分数,进而化为最简二次根式.
(2)原式中若有括号,要先去括号,再应用加法交换律、结合律将同类二次根式进行合并.
随堂演练
C
1. 与- 是同类二次根式的是( )
A. B. C. D.
2.计算3 -2 的结果是( )
A. B.2
C.3 D.6
A
3.若最简二次根式 与 可以进行合并,则m的值为( )
A.-1 B.0
C.1 D.2
D
4.下列二次根式
能与 合并的是____________;
能与 合并的是____________
5.计算:
解:
课堂小结
二次根式的加减
法则
注意
运算顺序
运算原理
一般地,二次根式的加减时,可以先将二次根式化成最简二次根式,再将同类二次根式进行合并.
运算律仍然适用
与实数的运算顺序一样
第16章 二次根式
16.2.2 第1课时 二次根式的加减
知识回顾
问题1 满足什么条件的根式是最简二次根式
(1)被开方数不含分母;
(2)被开方数中不含能开得尽方的因数或因式.
问题2 化简下列两组二次根式,每组化简后有什么共同特点
化简后被开方数相同
获取新知
如何进行二次根式的加减呢?
计算:
(化成最简二次根式)
(逆用乘法分配律)
同类二次根式:几个二次根式化成最简二次根式后,如果它们的被开方数相同,像这样的二次根式称为同类二次根式.
归纳总结
二次根式的加减法法则:
一般地,二次根式相加减,先把各个二次根式化成最简二次根式,再把同类二次根式进行合并.
(1)化——将非最简二次根式的二次根式化简;
二次根式加减法的运算步骤:
(2)找——找出同类二次根式;
(3)并——把同类二次根式的系数相加减,其他的不变.
即:
例题讲解
例1 下列根式中,不能与 合并的是( )
A. B. C. D.
C
导引:首先把选项中每个根式化成最简二次根式,然后找出被开方数不是3的二次根式.即
解:
例2 计算:
二次根式加减运算的技巧:
(1)将每个二次根式都化为最简二次根式,若被开方数中含有带分数,则要先化成假分数;若含有小数,则要化成分数,进而化为最简二次根式.
(2)原式中若有括号,要先去括号,再应用加法交换律、结合律将同类二次根式进行合并.
随堂演练
C
1. 与- 是同类二次根式的是( )
A. B. C. D.
2.计算3 -2 的结果是( )
A. B.2
C.3 D.6
A
3.若最简二次根式 与 可以进行合并,则m的值为( )
A.-1 B.0
C.1 D.2
D
4.下列二次根式
能与 合并的是____________;
能与 合并的是____________
5.计算:
解:
课堂小结
二次根式的加减
法则
注意
运算顺序
运算原理
一般地,二次根式的加减时,可以先将二次根式化成最简二次根式,再将同类二次根式进行合并.
运算律仍然适用
与实数的运算顺序一样
