沪科版数学八年级下册同步课件:16.2.1 第2课时 二次根式的除法
文档属性
| 名称 | 沪科版数学八年级下册同步课件:16.2.1 第2课时 二次根式的除法 |  | |
| 格式 | pptx | ||
| 文件大小 | 292.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-30 17:44:16 | ||
图片预览




文档简介
(共18张PPT)
第16章 二次根式
16.2.1 第2课时 二次根式的除法
情景导入
站在水平高度为h米的地方看到可见的水平距离为d米,它们近似地符合公式为 .
问题1 某一登山者爬到海拔100米处,即 时,他看到的水平线的距离d1是多少?
问题2 某一登山者爬到海拔200米处,即 时,他看到的水平线的距离d2是多少?
解:
解:
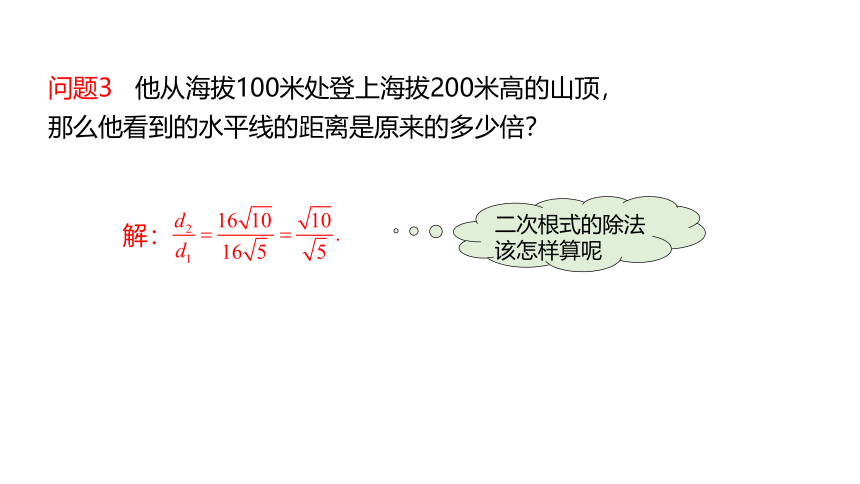
问题3 他从海拔100米处登上海拔200米高的山顶,那么他看到的水平线的距离是原来的多少倍?
解:
二次根式的除法该怎样算呢
获取新知
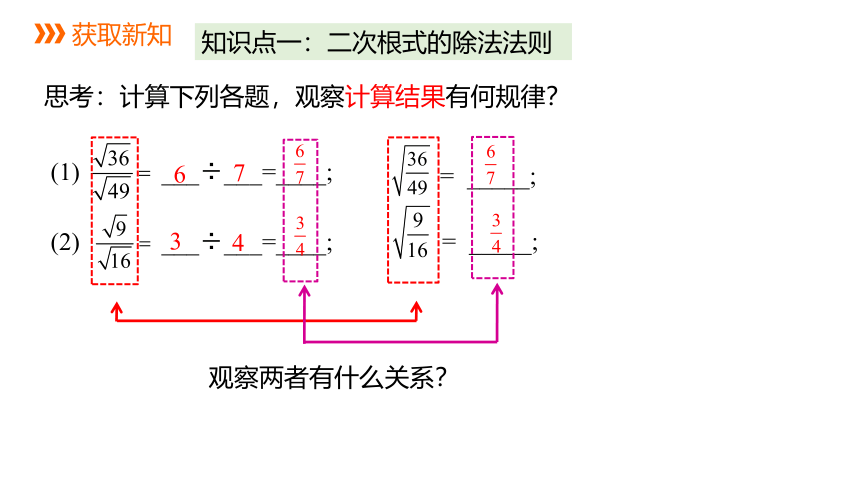
思考:计算下列各题,观察计算结果有何规律?
(1) ___÷___=____;
= _____;
(2) ___÷___=____;
= _____;
6
7
3
4
观察两者有什么关系?
知识点一:二次根式的除法法则
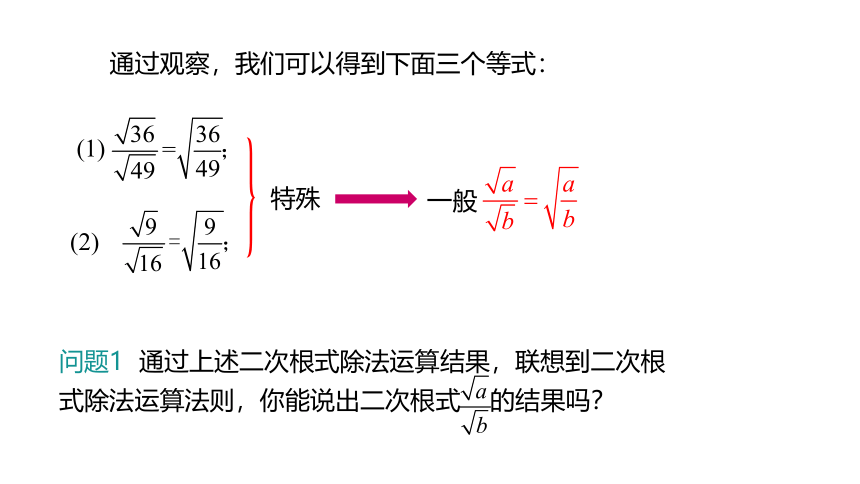
通过观察,我们可以得到下面三个等式:
(1)
(2)
问题1 通过上述二次根式除法运算结果,联想到二次根式除法运算法则,你能说出二次根式 的结果吗?
特殊
一般
问题2 在前面发现的规律 中,a,b的取值范围有没有限制呢?
① a,b同号
②同乘法法则一样,a,b都为非负数.
以上说法成立吗?为什么?
当a<0,b<0时,二次根式没有意义。
当b=0时,没有意义。
只有a≥0,b>0,才成立。
归纳总结
性质4:如果a≥0,b>0,那么有
文字语言:两个二次根式相除,把被开方数相除,根指数不变
证明:根据积的乘方法则,有
∴ .
就是 算术平方根.
又∵ 表示 算术平方根,
反过来:
一般的:
作用:我们可以运用它来进行二次根式的解题和化简.
文字语言:商的算术平方根等于被除式的算术平方根除以除式的算术平方根.
例题讲解
解:(1)方法一:
方法二:
例1 计算:
(1) ; (2)
若被开方数的分母不是完全平方数(式),依据分式的性质,分子分母同乘以一个数(或式),使之成为平方数(或式)
(2)
把分母中的根号化去,使分母变成有理数的这个过程就叫做分母有理化.
知识点二:分母有理化
获取新知
二次根式的除法运算中,通常采用分子、分母同乘以一个式子化去分母中的根号的方法来进行:
例2 计算:
解:
分母形如 的式子,分子、分母同乘以 可使分母不含根号.
例题讲解
分母有理化的一般步骤:
“一移”,即将分子、分母中能开得尽方的因数(式)移到根号外;
“二乘”,即将分子、分母同乘分母的有理化因数(式);
“三化”,即化简计算.
(1)被开方数不含分母,即为整数或整式;
(2)被开方数中不含能开得尽方的因数或因式.
我们把满足下列两个条件的二次根式,叫做最简二次根式.
随堂演练
1. 使 成立的x的取值范围是( )
A.x≠2 B.x≥0 C.x>2 D.x≥2
C
2.下列各式计算正确的是( )
A. B.
C. D.
C
3. 二次根式: , , , , , ,
其中是最简二次根式的有( )
A.1个 B.2个 C.3个 D.4个
C
4.计算:
解:
5. 在下列各式中,哪些是最简二次根式?哪些不是?对不是最简二次根式的进行化简.
解:只有(3)是最简二次根式;
课堂小结
二次根式除法
性质4
逆用
相关概念
分母有理化
最简二次根式
第16章 二次根式
16.2.1 第2课时 二次根式的除法
情景导入
站在水平高度为h米的地方看到可见的水平距离为d米,它们近似地符合公式为 .
问题1 某一登山者爬到海拔100米处,即 时,他看到的水平线的距离d1是多少?
问题2 某一登山者爬到海拔200米处,即 时,他看到的水平线的距离d2是多少?
解:
解:
问题3 他从海拔100米处登上海拔200米高的山顶,那么他看到的水平线的距离是原来的多少倍?
解:
二次根式的除法该怎样算呢
获取新知
思考:计算下列各题,观察计算结果有何规律?
(1) ___÷___=____;
= _____;
(2) ___÷___=____;
= _____;
6
7
3
4
观察两者有什么关系?
知识点一:二次根式的除法法则
通过观察,我们可以得到下面三个等式:
(1)
(2)
问题1 通过上述二次根式除法运算结果,联想到二次根式除法运算法则,你能说出二次根式 的结果吗?
特殊
一般
问题2 在前面发现的规律 中,a,b的取值范围有没有限制呢?
① a,b同号
②同乘法法则一样,a,b都为非负数.
以上说法成立吗?为什么?
当a<0,b<0时,二次根式没有意义。
当b=0时,没有意义。
只有a≥0,b>0,才成立。
归纳总结
性质4:如果a≥0,b>0,那么有
文字语言:两个二次根式相除,把被开方数相除,根指数不变
证明:根据积的乘方法则,有
∴ .
就是 算术平方根.
又∵ 表示 算术平方根,
反过来:
一般的:
作用:我们可以运用它来进行二次根式的解题和化简.
文字语言:商的算术平方根等于被除式的算术平方根除以除式的算术平方根.
例题讲解
解:(1)方法一:
方法二:
例1 计算:
(1) ; (2)
若被开方数的分母不是完全平方数(式),依据分式的性质,分子分母同乘以一个数(或式),使之成为平方数(或式)
(2)
把分母中的根号化去,使分母变成有理数的这个过程就叫做分母有理化.
知识点二:分母有理化
获取新知
二次根式的除法运算中,通常采用分子、分母同乘以一个式子化去分母中的根号的方法来进行:
例2 计算:
解:
分母形如 的式子,分子、分母同乘以 可使分母不含根号.
例题讲解
分母有理化的一般步骤:
“一移”,即将分子、分母中能开得尽方的因数(式)移到根号外;
“二乘”,即将分子、分母同乘分母的有理化因数(式);
“三化”,即化简计算.
(1)被开方数不含分母,即为整数或整式;
(2)被开方数中不含能开得尽方的因数或因式.
我们把满足下列两个条件的二次根式,叫做最简二次根式.
随堂演练
1. 使 成立的x的取值范围是( )
A.x≠2 B.x≥0 C.x>2 D.x≥2
C
2.下列各式计算正确的是( )
A. B.
C. D.
C
3. 二次根式: , , , , , ,
其中是最简二次根式的有( )
A.1个 B.2个 C.3个 D.4个
C
4.计算:
解:
5. 在下列各式中,哪些是最简二次根式?哪些不是?对不是最简二次根式的进行化简.
解:只有(3)是最简二次根式;
课堂小结
二次根式除法
性质4
逆用
相关概念
分母有理化
最简二次根式
