沪科版数学八年级下册同步课件:17.5 一元二次方程的应用
文档属性
| 名称 | 沪科版数学八年级下册同步课件:17.5 一元二次方程的应用 |

|
|
| 格式 | pptx | ||
| 文件大小 | 290.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-02 12:32:43 | ||
图片预览




文档简介
(共18张PPT)
第17章 一元二次方程
17.5 一元二次方程的应用
知识回顾
1.方程的实际应用常见问题有哪些呢?
2.确定这些实际问题的等量关系有什么方法吗?
常见的有数字问题,几何问题,变化率问题,销售问题等
数字问题:
三位数=百位数×100+十位数×10+个位数
几何问题:
常见规则几何图形的面积和体积(或容积)的计算公式
变化率问题:
现在量=原有量×(1±变化率)n
销售问题:
利润=售价-进价.
利润率= ×100% = ×100%.
售价=标价×折数×0.1
例题讲解
类型一:数字问题
例1 一个两位数,个位数字比十位数字大3,个位数字的平方刚好等于这个两位数,则这个两位数是多少?
解:设个位数字为x,那么十位数字是(x-3),这个两位数是10(x-3)+x,
依题意得:x2=10(x-3)+x,
∴x2-11x+30=0,
∴x1=5,x2=6,
∴x-3=2或3.
答:这个两位数是25或36.
关键在于多位数和各位数之间的关系和表示
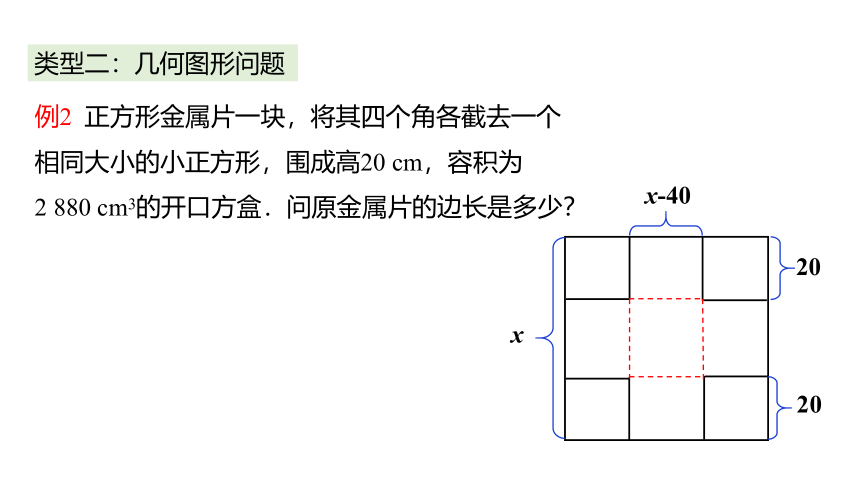
类型二:几何图形问题
例2 正方形金属片一块,将其四个角各截去一个相同大小的小正方形,围成高20 cm,容积为
2 880 cm3的开口方盒.问原金属片的边长是多少?
x
x-40
20
20
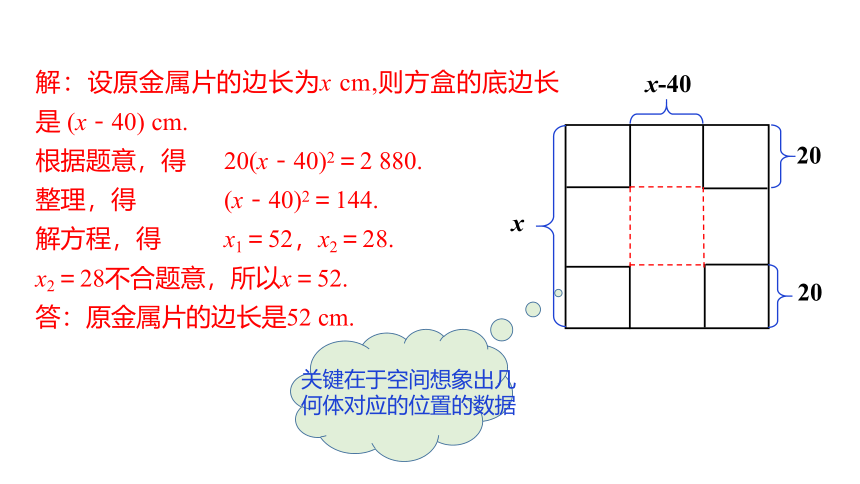
解:设原金属片的边长为x cm,则方盒的底边长是 (x-40) cm.
根据题意,得 20(x-40)2=2 880.
整理,得 (x-40)2=144.
解方程,得 x1=52,x2=28.
x2=28不合题意,所以x=52.
答:原金属片的边长是52 cm.
x
x-40
20
20
关键在于空间想象出几何体对应的位置的数据
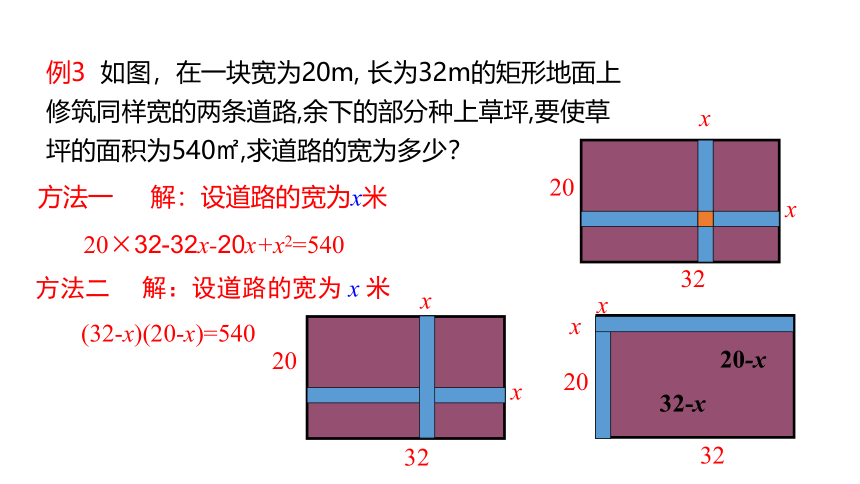
例3 如图,在一块宽为20m, 长为32m的矩形地面上修筑同样宽的两条道路,余下的部分种上草坪,要使草坪的面积为540㎡,求道路的宽为多少?
20
32
x
x
方法一 解:设道路的宽为x米
20×32-32x-20x+x2=540
20
32
x
x
方法二 解:设道路的宽为 x 米
(32-x)(20-x)=540
32
20
x
x
20-x
32-x
类型三:变化率问题
例4 原来每盒27元的一种药品,经过两次降价后每盒售价为9元.求该药品两次降价的平均降价率是多少?(精确到1%)
解:设该药品两次降价的平均降价率是x.根据题意得:
27(1-x)2=9
整理得:(1-x)2=1/3.
解这个方程得:x1≈1.58 , x2≈0.42.
结合题意 : x1≈1.58 不合题意,因此,只能取x≈0.42.
答:该药品两次降价的平均降价率是42%.
分析:设新品种花生产量的增长率为x,则新品种花生出油率的增长率为 ,根据新品种花生每公顷产量×新品种花生出油率=1980可列出方程.
例5 一农户原来种植的花生,每公顷的产量为3000㎏,出油率为50%(即每100㎏花生可加工出花生油50㎏).现在种植新品种花生后,每公顷收获的花生可加工出花生油1980㎏,已知花生出油率的增长率是产量增长率的 . 求新品种花生产量的增长率.
解:设设新品种花生产量的增长率为x,根据题意得:
3000×(1+x)[50%(1+ )]=1980
解方程得:
x1= 0.2=20% , x2=-3.2(不合题意,舍去).
答:新品种花生产量的增长率为20%
类型四:分式方程问题
例6 一组学生组织春游,预计共需费用120元.后来又有2人参加进来,费用不变,这样每人可少分摊3元.问原来这组学生的人数是多少
分析:设原来这组学生的人数是x人,则把体重信息整理成下表:
总费用/元 人数/人 每人费用/元
原来
现在
解:设原来这组学生的人数是x人,由题意得,
两边同乘x(x+2),整理,得,
x2+2x-80=0.
解这个方程,得,
x1=-10,x2=8.
经检验x1=-10,x2=8都是原方程的根,但x1=-10不符合题意,所以取x=8.
答:原来这组学生是8人.
随堂演练
1. 一个两位数,个位上的数字比十位上的数字小4,且个位数字与十位数字的平方和比这个两位数小4.若设个位数字为x,则根据题意可列方程为( )
A.x2+(x-4)2=10(x-4)+x-4
B.x2+(x+4)2=10x+(x-4)-4
C.x2+(x+4)2=10(x+4)+x-4
D.x2+(x-4)2=10x+(x-4)-4
D
2. 如图所示的是一块长方形花园,其宽(短边)为20 m,现打算将花园扩建,要求长边保持不变,将短边扩大到与长边相等,使得扩建后的花园是正方形,若扩大后的花园面积比原来增加了100 m2,设长方形的长边为x m,则可列方程为( )
A.x(x-20)=100 B.x(x+20)=100
C.20x=100 D.(x+20)(x-20)=100
A
3. 某种品牌运动服经过两次降价,每件零售价由a元降为b元,已知两次降价的百分率相同,求每次降价的百分率.设每次降价的百分率为x,下面所列的方程中正确的是( )
A.a(1+x)2=b B.a(1-x)2=b
C.a(1-2x)2=b D.a(1-x2)=b
B
4. 某商品现在的售价是每件130元,每日的销售量是70件.市场调查反映:若每件商品售价涨1元,每日的销售量就减少1件.已知商品的进价是每件120元,那么商品定价为多少元时,每日盈利1600元
解:设每件商品涨价x元,
(1)用含x的代数式表示:
①销售价为 元;
②日销售量为 件.
(2)根据题意,列出相应方程为 .
(3)解这个方程,得 .
(4)130+x= .
(5)答:每件商品定价为 元时,每日盈利1600元.
(130+x)
(70-x)
(130+x-120)(70-x)=1600
x1=x2=30
160
160
5. 某空调厂的装配车间,原计划用若干天组装150台空调,厂家为了使空调提前上市,决定每天多组装3台,这样提前3天超额完成了任务,总共比原计划多组装6台,问原计划每天组装多少台
解:设原计划每天组装x台.依题意,得
化简得x2+5x-150=0,
解得x1=-15,x2=10.
经检验x1=-15,x2=10均是原方程的解,
但x1=-15不合题意,舍去.
答:原计划每天组装10台.
课堂小结
一元二次方程的应用
增长率
a(1+x)2=b,其中a为增长前的量,x为增长率,2为增长次数,b为增长后的量.
降低率
a(1-x)2=b,其中a为降低前的量,x为降低率,2为降低次数,b为降低后的量.注意1与x位置不可调换.
平均变化率问题
几何图形
几何图形面积、体积是等量关系.(转化和想象能力)
数字问题
如三位数=百位数×100+十位数×10+个位数
第17章 一元二次方程
17.5 一元二次方程的应用
知识回顾
1.方程的实际应用常见问题有哪些呢?
2.确定这些实际问题的等量关系有什么方法吗?
常见的有数字问题,几何问题,变化率问题,销售问题等
数字问题:
三位数=百位数×100+十位数×10+个位数
几何问题:
常见规则几何图形的面积和体积(或容积)的计算公式
变化率问题:
现在量=原有量×(1±变化率)n
销售问题:
利润=售价-进价.
利润率= ×100% = ×100%.
售价=标价×折数×0.1
例题讲解
类型一:数字问题
例1 一个两位数,个位数字比十位数字大3,个位数字的平方刚好等于这个两位数,则这个两位数是多少?
解:设个位数字为x,那么十位数字是(x-3),这个两位数是10(x-3)+x,
依题意得:x2=10(x-3)+x,
∴x2-11x+30=0,
∴x1=5,x2=6,
∴x-3=2或3.
答:这个两位数是25或36.
关键在于多位数和各位数之间的关系和表示
类型二:几何图形问题
例2 正方形金属片一块,将其四个角各截去一个相同大小的小正方形,围成高20 cm,容积为
2 880 cm3的开口方盒.问原金属片的边长是多少?
x
x-40
20
20
解:设原金属片的边长为x cm,则方盒的底边长是 (x-40) cm.
根据题意,得 20(x-40)2=2 880.
整理,得 (x-40)2=144.
解方程,得 x1=52,x2=28.
x2=28不合题意,所以x=52.
答:原金属片的边长是52 cm.
x
x-40
20
20
关键在于空间想象出几何体对应的位置的数据
例3 如图,在一块宽为20m, 长为32m的矩形地面上修筑同样宽的两条道路,余下的部分种上草坪,要使草坪的面积为540㎡,求道路的宽为多少?
20
32
x
x
方法一 解:设道路的宽为x米
20×32-32x-20x+x2=540
20
32
x
x
方法二 解:设道路的宽为 x 米
(32-x)(20-x)=540
32
20
x
x
20-x
32-x
类型三:变化率问题
例4 原来每盒27元的一种药品,经过两次降价后每盒售价为9元.求该药品两次降价的平均降价率是多少?(精确到1%)
解:设该药品两次降价的平均降价率是x.根据题意得:
27(1-x)2=9
整理得:(1-x)2=1/3.
解这个方程得:x1≈1.58 , x2≈0.42.
结合题意 : x1≈1.58 不合题意,因此,只能取x≈0.42.
答:该药品两次降价的平均降价率是42%.
分析:设新品种花生产量的增长率为x,则新品种花生出油率的增长率为 ,根据新品种花生每公顷产量×新品种花生出油率=1980可列出方程.
例5 一农户原来种植的花生,每公顷的产量为3000㎏,出油率为50%(即每100㎏花生可加工出花生油50㎏).现在种植新品种花生后,每公顷收获的花生可加工出花生油1980㎏,已知花生出油率的增长率是产量增长率的 . 求新品种花生产量的增长率.
解:设设新品种花生产量的增长率为x,根据题意得:
3000×(1+x)[50%(1+ )]=1980
解方程得:
x1= 0.2=20% , x2=-3.2(不合题意,舍去).
答:新品种花生产量的增长率为20%
类型四:分式方程问题
例6 一组学生组织春游,预计共需费用120元.后来又有2人参加进来,费用不变,这样每人可少分摊3元.问原来这组学生的人数是多少
分析:设原来这组学生的人数是x人,则把体重信息整理成下表:
总费用/元 人数/人 每人费用/元
原来
现在
解:设原来这组学生的人数是x人,由题意得,
两边同乘x(x+2),整理,得,
x2+2x-80=0.
解这个方程,得,
x1=-10,x2=8.
经检验x1=-10,x2=8都是原方程的根,但x1=-10不符合题意,所以取x=8.
答:原来这组学生是8人.
随堂演练
1. 一个两位数,个位上的数字比十位上的数字小4,且个位数字与十位数字的平方和比这个两位数小4.若设个位数字为x,则根据题意可列方程为( )
A.x2+(x-4)2=10(x-4)+x-4
B.x2+(x+4)2=10x+(x-4)-4
C.x2+(x+4)2=10(x+4)+x-4
D.x2+(x-4)2=10x+(x-4)-4
D
2. 如图所示的是一块长方形花园,其宽(短边)为20 m,现打算将花园扩建,要求长边保持不变,将短边扩大到与长边相等,使得扩建后的花园是正方形,若扩大后的花园面积比原来增加了100 m2,设长方形的长边为x m,则可列方程为( )
A.x(x-20)=100 B.x(x+20)=100
C.20x=100 D.(x+20)(x-20)=100
A
3. 某种品牌运动服经过两次降价,每件零售价由a元降为b元,已知两次降价的百分率相同,求每次降价的百分率.设每次降价的百分率为x,下面所列的方程中正确的是( )
A.a(1+x)2=b B.a(1-x)2=b
C.a(1-2x)2=b D.a(1-x2)=b
B
4. 某商品现在的售价是每件130元,每日的销售量是70件.市场调查反映:若每件商品售价涨1元,每日的销售量就减少1件.已知商品的进价是每件120元,那么商品定价为多少元时,每日盈利1600元
解:设每件商品涨价x元,
(1)用含x的代数式表示:
①销售价为 元;
②日销售量为 件.
(2)根据题意,列出相应方程为 .
(3)解这个方程,得 .
(4)130+x= .
(5)答:每件商品定价为 元时,每日盈利1600元.
(130+x)
(70-x)
(130+x-120)(70-x)=1600
x1=x2=30
160
160
5. 某空调厂的装配车间,原计划用若干天组装150台空调,厂家为了使空调提前上市,决定每天多组装3台,这样提前3天超额完成了任务,总共比原计划多组装6台,问原计划每天组装多少台
解:设原计划每天组装x台.依题意,得
化简得x2+5x-150=0,
解得x1=-15,x2=10.
经检验x1=-15,x2=10均是原方程的解,
但x1=-15不合题意,舍去.
答:原计划每天组装10台.
课堂小结
一元二次方程的应用
增长率
a(1+x)2=b,其中a为增长前的量,x为增长率,2为增长次数,b为增长后的量.
降低率
a(1-x)2=b,其中a为降低前的量,x为降低率,2为降低次数,b为降低后的量.注意1与x位置不可调换.
平均变化率问题
几何图形
几何图形面积、体积是等量关系.(转化和想象能力)
数字问题
如三位数=百位数×100+十位数×10+个位数
