人教版八年级数学 下册 第十九章 19.1.2 函数的图像 第2课时 函数的表示法 课件(共20张PPT)
文档属性
| 名称 | 人教版八年级数学 下册 第十九章 19.1.2 函数的图像 第2课时 函数的表示法 课件(共20张PPT) | 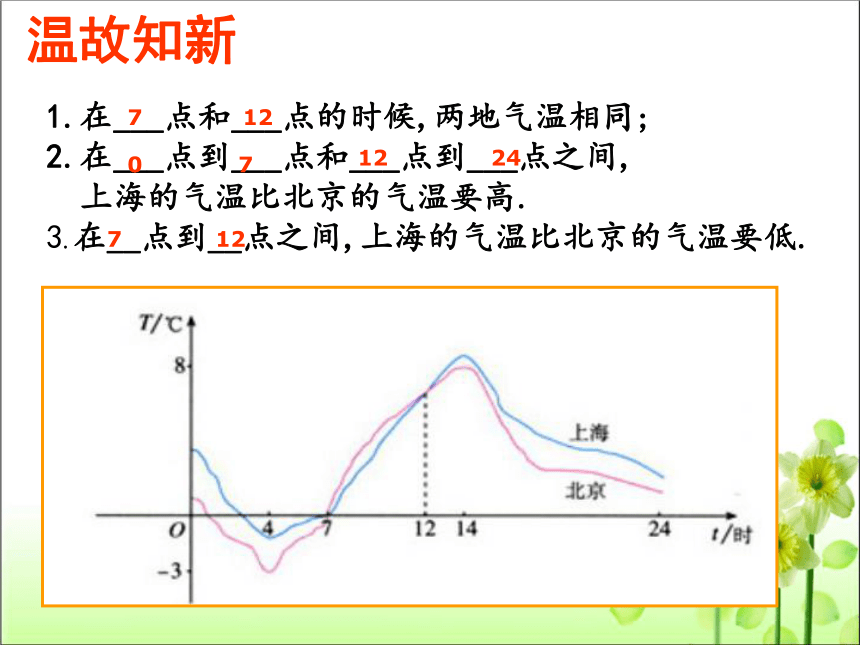 | |
| 格式 | zip | ||
| 文件大小 | 540.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-01 10:42:48 | ||
图片预览






文档简介
(共20张PPT)
温故知新
1.在___点和___点的时候,两地气温相同;
2.在___点到___点和___点到___点之间,
上海的气温比北京的气温要高.
3.在__点到__点之间,上海的气温比北京的气温要低.
7
12
7
12
0 7
12 24
19.1.2 函数的图像
第2课时 函数的表示法
人教版八年级数学 下册
情境引入
学习目标
1.了解函数的三种表示方法及其优点;
2.能用适当的方式表示简单实际问题中的变量之间
的函数关系;(重点)
3.能对函数关系进行分析,对变量的变化情况进行
初步讨论.(难点)
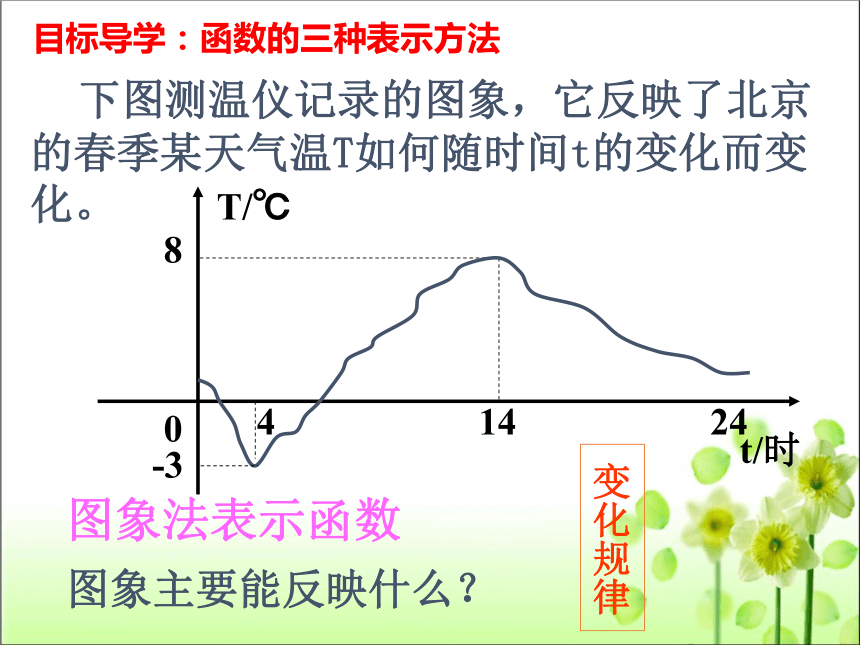
下图测温仪记录的图象,它反映了北京的春季某天气温T如何随时间t的变化而变化。
4
14
24
t/时
8
T/℃
0
图象法表示函数
图象主要能反映什么?
-3
变化规律
目标导学:函数的三种表示方法
列表法表示函数
表格主要能反映对应关系
2、 下表是某种股票一周内周一至周五的收盘价。
12
收盘价
星期五
星期四
星期三
星期二
星期一
时间
12.5
12.9
12.45
12.75
3、 汽车以60千米/时的速度匀速行驶,行驶里程为 s 千米,行驶时间为t 小时,写出s与t的函数解析式。
S = 60t
解析式法表示函数
解析式主要能反映数量关系
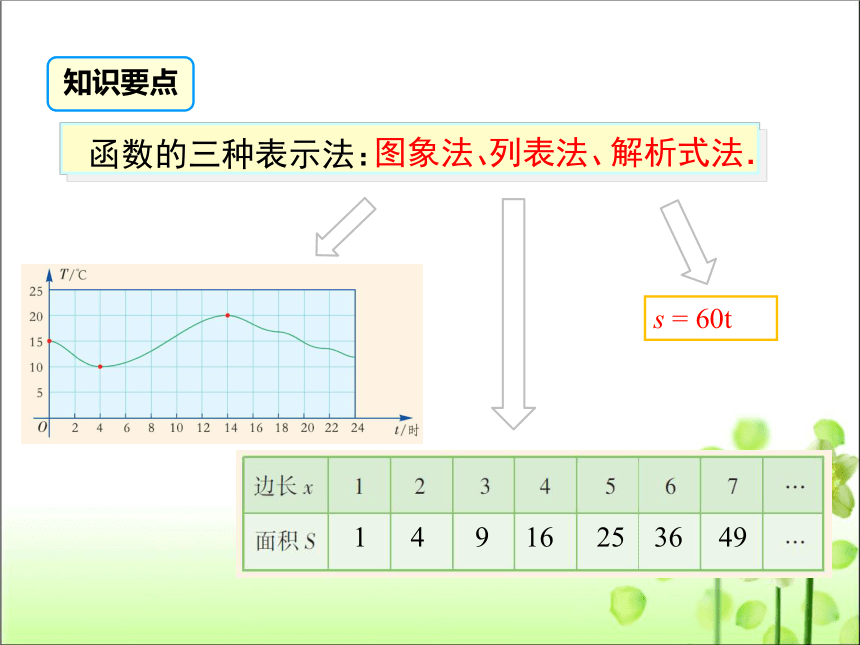
函数的三种表示法:
s = 60t
图象法、
列表法、
解析式法.
1 4 9 16 25 36 49
知识要点
例 1.如图,要做一个面积为12 m2的小花坛,该花坛的一边长为 x m,周长为 y m.
(1)变量 y 是变量 x 的函数吗?如果是,写出自变量的取值范围;
(2)能求出这个问题的函数解析式吗?
x
解:(1)y 是 x 的函数,自变量 x 的取值范围是x>0.
(2)y =2(x + )
典例精析
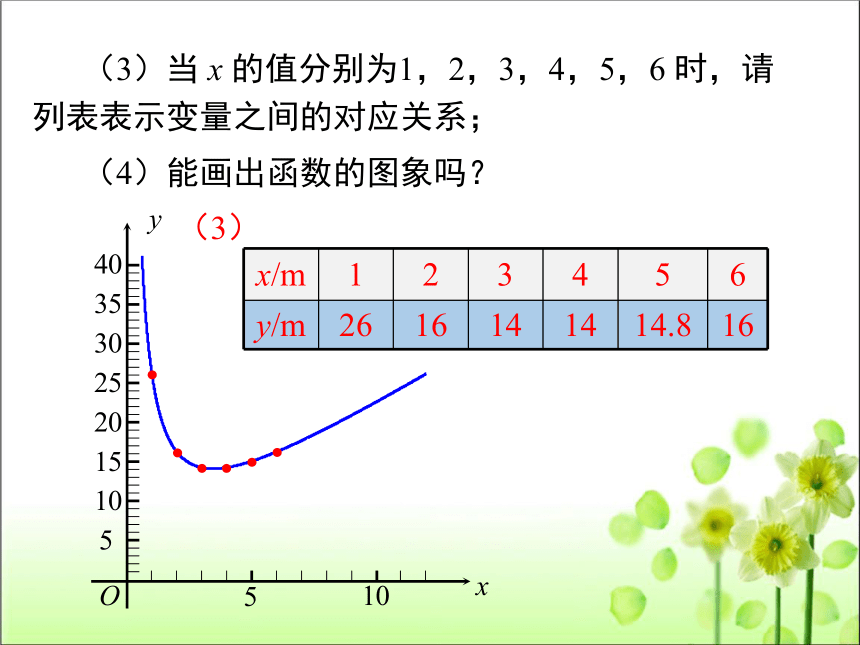
(3)当 x 的值分别为1,2,3,4,5,6 时,请列表表示变量之间的对应关系;
(4)能画出函数的图象吗?
x/m 1 2 3 4 5 6
y/m 26 16 14 14 14.8 16
40
35
30
25
20
15
10
5
5
10
O
x
y
(3)
1.解析式法:准确地反映了函数与自变量之间的数量关系.
2.列表法:具体地反映了函数与自变量的数值对应关系.
3.图象法:直观地反映了函数随自变量的变化而变化的规律.
议一议
这三种表示函数的方法各有什么优点?
例2
某年初,我国西南部分省市遭
遇了严重干旱.某水库的蓄水
量随着时间的增加而减小,干
旱持续时间t(天)与蓄水量V(万
立方米)的变化情况如图所示,
根据图象回答问题:
(1)这个图象反映了哪两个变量之间的关系?
(2)根据图象填表:
(3)当t取0至60天之间的任一值时,对应几个V值?
(4)V可以看作t的函数吗?若可以,写出函数解析式.
干旱持续时间t/天 0 10 20 30 40 50 60
蓄水量V/万立方米
(1)通过读图可知,横坐标表示干旱持续时间,纵坐标表
示水库蓄水量,因此它表示的是干旱持续时间与水库
蓄水量之间的关系;
(2)根据图象信息确定每个特殊点的坐标即可;
(3)观察图象可得;
(4)可根据函数的定义来判断.
(1)图象反映了干旱持续时间与水库蓄水量之间的关系.
(2)填表如下:
导引:
解:
干旱持续时间t/天 0 10 20 30 40 50 60
蓄水量V/万立方米 1 200 1 000 800 600 400 200 0
(3)当t取0至60天之间的任一值时,对应着一个V值.
(4)V可以看作t的函数.
根据图象可知,该水库初始蓄水量为1 200万立方米,
干旱每持续10天,蓄水量相应减少200万立方米,由
此可得出函数解析式为
V=1 200- =-20t+1 200(0≤t≤60).
课堂小结
函数的表示方法
解析式法:反映了函数与自变量之间的数量关系
列表法:反映了函数与自变量的数值对应关系
图象法:反映了函数随自变量的变化而变化的规律
1.要形象、直观地表示某市某天的气温与时间的函数关系,适宜用( )
A.列表法 B.解析式法
C.图象法 D.以上都可以
目标检测
C
2.柿子熟了,从树上落下来.下面的哪一幅图可以大致刻画出柿子下落过程中的速度变化情况 ( )
O
速度
时间
A
O
速度
时间
D
O
速度
时间
C
O
速度
时间
B
C
目标检测
3.夏季高山上温度从山脚起每升高100米降低 0.6℃,已知山脚下温度是23℃,则温度y( ℃ )与上升高度 x(m)之间的函数关系式 ,若某种植物适宜生长的度为17 ℃y =23-0.006x
500< x <1000
目标检测
4.用列表法与解析式法表示n边形的内角和m(单位:度)是边数n的函数.
解:因为n表示的是多边形的边数,所以n是大于等于3的自然数,列表如下:
n 3 4 5 6 …
m …
所以m=(n-2)·180°(n≥3,且n为自然数).
180
360
540
720
提示:n边形的内角和公式是:(n-2) ×180°.
目标检测
通过本课学习,你收获了什么?
温故知新
1.在___点和___点的时候,两地气温相同;
2.在___点到___点和___点到___点之间,
上海的气温比北京的气温要高.
3.在__点到__点之间,上海的气温比北京的气温要低.
7
12
7
12
0 7
12 24
19.1.2 函数的图像
第2课时 函数的表示法
人教版八年级数学 下册
情境引入
学习目标
1.了解函数的三种表示方法及其优点;
2.能用适当的方式表示简单实际问题中的变量之间
的函数关系;(重点)
3.能对函数关系进行分析,对变量的变化情况进行
初步讨论.(难点)
下图测温仪记录的图象,它反映了北京的春季某天气温T如何随时间t的变化而变化。
4
14
24
t/时
8
T/℃
0
图象法表示函数
图象主要能反映什么?
-3
变化规律
目标导学:函数的三种表示方法
列表法表示函数
表格主要能反映对应关系
2、 下表是某种股票一周内周一至周五的收盘价。
12
收盘价
星期五
星期四
星期三
星期二
星期一
时间
12.5
12.9
12.45
12.75
3、 汽车以60千米/时的速度匀速行驶,行驶里程为 s 千米,行驶时间为t 小时,写出s与t的函数解析式。
S = 60t
解析式法表示函数
解析式主要能反映数量关系
函数的三种表示法:
s = 60t
图象法、
列表法、
解析式法.
1 4 9 16 25 36 49
知识要点
例 1.如图,要做一个面积为12 m2的小花坛,该花坛的一边长为 x m,周长为 y m.
(1)变量 y 是变量 x 的函数吗?如果是,写出自变量的取值范围;
(2)能求出这个问题的函数解析式吗?
x
解:(1)y 是 x 的函数,自变量 x 的取值范围是x>0.
(2)y =2(x + )
典例精析
(3)当 x 的值分别为1,2,3,4,5,6 时,请列表表示变量之间的对应关系;
(4)能画出函数的图象吗?
x/m 1 2 3 4 5 6
y/m 26 16 14 14 14.8 16
40
35
30
25
20
15
10
5
5
10
O
x
y
(3)
1.解析式法:准确地反映了函数与自变量之间的数量关系.
2.列表法:具体地反映了函数与自变量的数值对应关系.
3.图象法:直观地反映了函数随自变量的变化而变化的规律.
议一议
这三种表示函数的方法各有什么优点?
例2
某年初,我国西南部分省市遭
遇了严重干旱.某水库的蓄水
量随着时间的增加而减小,干
旱持续时间t(天)与蓄水量V(万
立方米)的变化情况如图所示,
根据图象回答问题:
(1)这个图象反映了哪两个变量之间的关系?
(2)根据图象填表:
(3)当t取0至60天之间的任一值时,对应几个V值?
(4)V可以看作t的函数吗?若可以,写出函数解析式.
干旱持续时间t/天 0 10 20 30 40 50 60
蓄水量V/万立方米
(1)通过读图可知,横坐标表示干旱持续时间,纵坐标表
示水库蓄水量,因此它表示的是干旱持续时间与水库
蓄水量之间的关系;
(2)根据图象信息确定每个特殊点的坐标即可;
(3)观察图象可得;
(4)可根据函数的定义来判断.
(1)图象反映了干旱持续时间与水库蓄水量之间的关系.
(2)填表如下:
导引:
解:
干旱持续时间t/天 0 10 20 30 40 50 60
蓄水量V/万立方米 1 200 1 000 800 600 400 200 0
(3)当t取0至60天之间的任一值时,对应着一个V值.
(4)V可以看作t的函数.
根据图象可知,该水库初始蓄水量为1 200万立方米,
干旱每持续10天,蓄水量相应减少200万立方米,由
此可得出函数解析式为
V=1 200- =-20t+1 200(0≤t≤60).
课堂小结
函数的表示方法
解析式法:反映了函数与自变量之间的数量关系
列表法:反映了函数与自变量的数值对应关系
图象法:反映了函数随自变量的变化而变化的规律
1.要形象、直观地表示某市某天的气温与时间的函数关系,适宜用( )
A.列表法 B.解析式法
C.图象法 D.以上都可以
目标检测
C
2.柿子熟了,从树上落下来.下面的哪一幅图可以大致刻画出柿子下落过程中的速度变化情况 ( )
O
速度
时间
A
O
速度
时间
D
O
速度
时间
C
O
速度
时间
B
C
目标检测
3.夏季高山上温度从山脚起每升高100米降低 0.6℃,已知山脚下温度是23℃,则温度y( ℃ )与上升高度 x(m)之间的函数关系式 ,若某种植物适宜生长的度为17 ℃
500< x <1000
目标检测
4.用列表法与解析式法表示n边形的内角和m(单位:度)是边数n的函数.
解:因为n表示的是多边形的边数,所以n是大于等于3的自然数,列表如下:
n 3 4 5 6 …
m …
所以m=(n-2)·180°(n≥3,且n为自然数).
180
360
540
720
提示:n边形的内角和公式是:(n-2) ×180°.
目标检测
通过本课学习,你收获了什么?
