山东省菏泽市郓城县2021-2022学年九年级下学期期中考试数学试题(pdf版含答案)
文档属性
| 名称 | 山东省菏泽市郓城县2021-2022学年九年级下学期期中考试数学试题(pdf版含答案) |

|
|
| 格式 | |||
| 文件大小 | 514.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-02 00:00:00 | ||
图片预览




文档简介
2021——2022 学年度第二学期期中教学质量检测
九年级数学试题
(满分 120 分,时间:120 分钟)
一、选择题:本大题共 8 个小题,每小题 3 分,共 24 分,在每小题给出的四个选项 A、B、C、
D 中,只有一项是正确的,请把正确的选项填在答题卡的相应位置
1.在疫情防控的特殊时期,为了满足初三高三学生的复习备考需求,菏泽市教委联合菏泽卫
视共同推出电视课堂节目:“空中课堂”,在节目播出期间.全市约有 200000 名师生收看
了节目.将 200000 用科学记数法表示应为
5 6 5 6
A.0.2×10 B.0.2×10 C.2×10 D.2×10
2.下列图形中,是轴对称图形的是
A. B. C. D.
3.A、B 是数轴上位于原点 O 异侧的两点(点 A 在点 B 的左侧),若点 A、B 分别对应的实数
为 a、b,且|a|>|b|,则 a、-a、b、-b 中最大的数是
A.a B.-a C.b D. -b
4.如图,该立体图形的俯视图是
A. B. C. D.
第 5题图
5. 如图,三角板的直角顶点落在矩形纸片的一边上.若
∠1=35°,则∠2 的度数是
A.35° B.55° C.45° D.65°
2 a 1 a6.如果 a a 1 0,那么代数式 1 2 的值是 a 2a 1 a 1
第 7 题图
A. 3 B. 1 C. -1 D. -3
7.小明收集了鄂尔多斯市某酒店 2022 年 3 月 1 日~3 月 6 日每天的用水量(单位:吨),整
理并绘制成如图所示的折线统计图,下列结论正确的是
23 25
A.平均数是 B.众数是 10 C.中位数是 8.5 D.方差是
4 3
8.如图,在平面直角坐标系中,菱形ABCD 在第一象限内,
边BC 与x 轴平行,A、B 两点的纵坐标分别为4、1,反比例
函数 y k= 的图象经过 A、B 两点,菱形ABCD 的面积为9 2 , 第 8 题图
x
1
则k 的值为
A.4 B.5 C.6 D.9
二、填空题(本大题共 6个小题,每小题 3 分,共 18 分,只要求
三、把最后的结果填写在答题卡的相应区域内)
9.因式分解:4a2b-b ;
10.如图 A'B'∥AB,B'C'∥BC,且 OA':A'A=4:3,则△ABC 与△A'B'C'是位似图形,△ABC 与△A'B'C'
的位似比为 ;
第13题图 第 14 题图第 10 题图
11.若 a、b、c 的方差为 3,则 2a+3、2b+3、2c+3 的方差为_ ;
12.设 m,n 是方程 x2-2x-2022=0 的两个实数根,则 m2-m+n 的值为_____;
13.如图,正方形 ABCD 中,扇形 ABC 与扇形 BCD 的弧交于点 E,AB=2cm,则图中阴影部分的
面积为 cm2;(不求近似值)
2
14.如图,若二次函数 y=ax +bx+c(a≠0)的图象的对称轴为直线 x=1,与 y 轴交于点 C,与
x轴交于点 A、点 B(-1,0),则下列结论:①abc>0; ②二次函数的最大值为 a+b+c;
2
③a-b+c<0;④b -4ac<0;⑤当 y>0 时,-1三、解答题(本大题共 78 分.把解答和证明过程写在答题卡的相应区域内)
0.04 +cos2 45O -1 115.(6 分) 计算: - 2 + | - |
2
2 3 x -3 x +6
16.(6 分)已知 x +3x-3=0,求代数式(1- ) - 的值.
x x +3 x +3
0
17.(6 分) 如图,在 Rt△ABC 中,∠C=90 ,AB 的垂直平分线交 AC 于 第17题图
点 D,交 AB 于点 E.(1)求证:△ADE∽△ABC;(2)当 AC=8,BC=6 时,求 DE 的长.
18.(6 分)为了更好的收治新冠肺炎患者,某市计划用 810 米的建筑材料在一个空地上搭建方
舱医院,如图所示是医院的平面图,医院分为三个区,矩形 BFHG 区用于隔离治疗重症患者,
矩形 CDEF 区用于隔离治疗轻症患者,医护室是正方形 AGHE,已知围成轻症患者区的建筑材
料与围成医护室、重症患者区的建筑材料之和一样多,设 AE=x 米.
(1)用含 x 的代数式表示:DE= 米,AB= 米;
(2)设矩形 BFHG 的面积为 6075 平方米,求 AE 的长.
第18题图
2
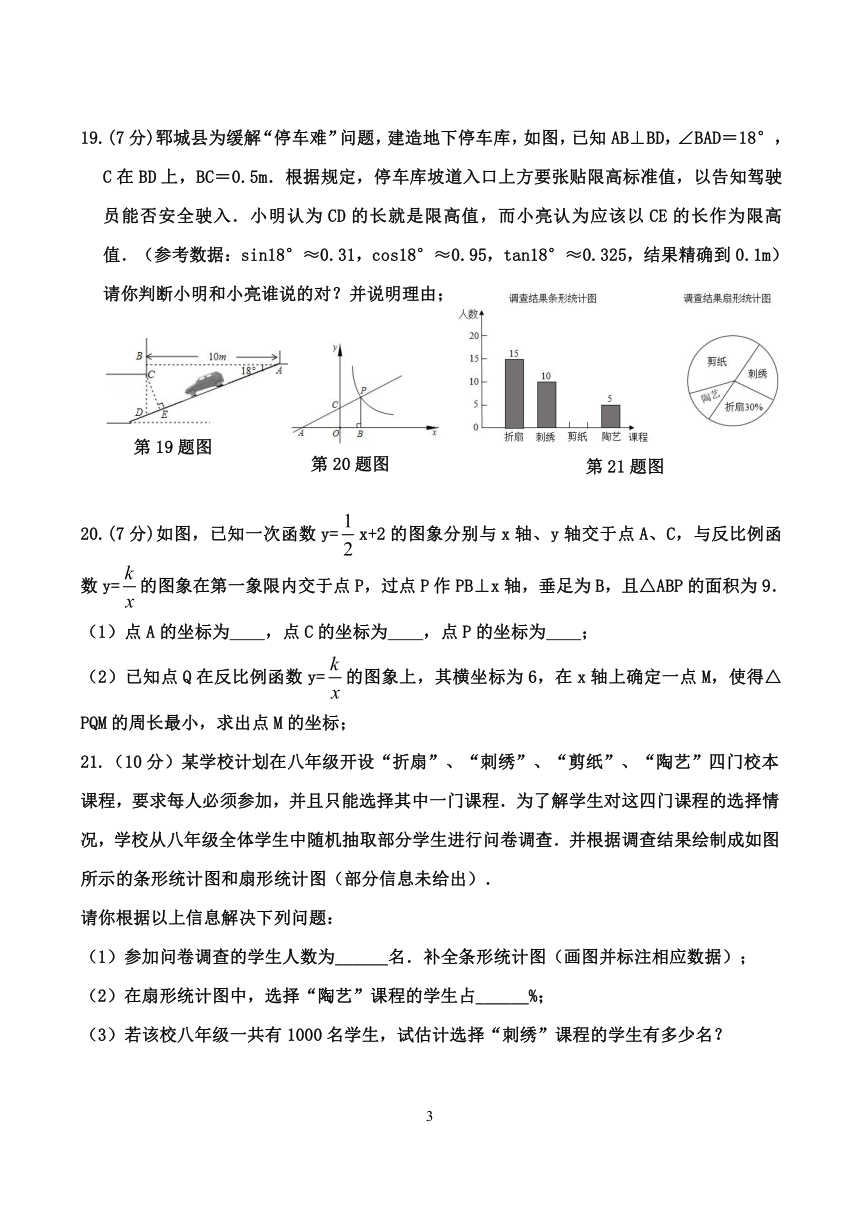
19.(7 分)郓城县为缓解“停车难”问题,建造地下停车库,如图,已知 AB⊥BD,∠BAD=18°,
C 在 BD 上,BC=0.5m.根据规定,停车库坡道入口上方要张贴限高标准值,以告知驾驶
员能否安全驶入.小明认为 CD 的长就是限高值,而小亮认为应该以 CE 的长作为限高
值.(参考数据:sin18°≈0.31,cos18°≈0.95,tan18°≈0.325,结果精确到 0.1m)
请你判断小明和小亮谁说的对?并说明理由;
第 19 题图
第 20 题图 第 21 题图
1
20.(7 分)如图,已知一次函数 y= x+2 的图象分别与 x 轴、y 轴交于点 A、C,与反比例函
2
k
数 y= 的图象在第一象限内交于点 P,过点 P作 PB⊥x 轴,垂足为 B,且△ABP 的面积为 9.
x
(1)点 A 的坐标为 ,点 C的坐标为 ,点 P 的坐标为 ;
k
(2)已知点 Q 在反比例函数 y= 的图象上,其横坐标为 6,在 x 轴上确定一点 M,使得△
x
PQM 的周长最小,求出点 M 的坐标;
21.(10 分)某学校计划在八年级开设“折扇”、“刺绣”、“剪纸”、“陶艺”四门校本
课程,要求每人必须参加,并且只能选择其中一门课程.为了解学生对这四门课程的选择情
况,学校从八年级全体学生中随机抽取部分学生进行问卷调查.并根据调查结果绘制成如图
所示的条形统计图和扇形统计图(部分信息未给出).
请你根据以上信息解决下列问题:
(1)参加问卷调查的学生人数为______名.补全条形统计图(画图并标注相应数据);
(2)在扇形统计图中,选择“陶艺”课程的学生占______%;
(3)若该校八年级一共有 1000 名学生,试估计选择“刺绣”课程的学生有多少名?
3
22.(10 分) 如图,DB 过 O 的圆心,交 O 于点 A、B,DC 是 O 的切线,点 C 是切点,
0
已知∠D=30 ,DC= 3.(1)求证:△BOC∽△BCD;(2)求△BCD 的周长.
第 22 题图
23.(10 分)如图 1,在正方形 ABCD 中,点 E 是 CD 上一动点,将正方形沿着 BE 折叠,点 C
落在点 F 处,连结 BE,CF,延长 CF 交 AD 于点 G.
(1)求证:△BCE≌△CDG.
HD 4
(2)如图 2,在(1)的条件下,延长 BF 交 AD 于点 H.若 ,CE=9,求线段 DE 的长.
HF 5
第23题图
1 2
24.(10 分)如图,抛物线 y=- x +bx+c 与 x 轴交于 A(-1,0),B(4,0),与 y 轴交于点 C.连
2
接 AC,BC,点 P 在抛物线上运动.
(1)求抛物线的表达式;
(2)若点 P 在第四象限,点 Q 在 PA 的延长线上,
当∠CAQ=∠CBA 45°时,求点 P 的坐标; 第24题图
4
2021——2022 学年度第二学期期中教学质量检测
九年级数学试题参考答案
一、选择题答题栏(每小题选对得 3 分,共 24 分)
题号 1 2 3 4 5 6 7 8
答案 C D B C B A D A
二、填空题:(每小题选对得 3 分,共 18 分)
9. b(2a+1)(2a-1) 10. 7:4 11. 12 12.2024 13. 14.②⑤⑥
3
三、解答题:本大题共 10 小题,共 78 分.解答要写出必要的文字说明、证明过程或演算步
骤
2 0 -1 1
15.(6 分)解: 0.04 +cos 45 - 2 + | - |
2
2 1 1
=0.2+( )2 - + …………………………………………………4 分
2 2 2
1 1 1
=0.2+ - +
2 2 2
=0.7……………………………………………………………………6 分
3 x -3 x +6
16.(6 分)解:(1- ) -
x x +3 x +3
x - 3 x - 3 x +6
= - …………………………………………………………1 分
x x +3 x +3
x - 3 x+3 x +6
= -
x x - 3 x +3
x+3 x +6
= - …………………………………………………………………3 分
x x +3
(x+3)2 - x(x +6)
=
(x x+3)
9
= 2 ………………………………………………………………………4 分x +3x
2
∵x +3x-3=0
2
∴x +3x=3………………………………………………………………………5 分
5
9
则原式= 2 =3………………………………………………………………6 分x +3x
17.(6 分)证明:(1) ∵DE垂直平分 AB ,
∴ AED 90 .
∴ AED C .
∵ A A,
∴△ADE∽△ABC…………………………………………………………3 分
(2) Rt△ABC中, AC 8, BC 6,
∴ AB 10.
∵DE平分 AB,
∴ AE 5.
∵△ADE∽△ABC,
DE AE
∴ .
BC AC
DE 5
∴ .
6 8
DE 15∴ ………………………………………………………………6 分
4
18.(6 分)解:(1)∵四边形 ABCD 为矩形,
∴AB=CD,
∵围成轻症患者区的建筑材料与围成医护室、重症患者区的建筑材料之和一样多,
∴AE+GH+BF=DE+CF,
即 3AE=2DE.
3
设 AE=x 米,则 DE= x 米.
2
∵搭建方舱医院的材料总长度为 810 米,
810 -3AE - 2DE 810 -3x - 2
3
x
∴AB= = 2 (270﹣2x)米.
3 3
3
故答案为: x米;(270﹣2x)米.………………………………………2 分
2
(2)∵四边形 AGHE 为正方形,
6
∴AG=AE=x 米,
∴BG=AB﹣AG=270﹣2x﹣x=(270﹣3x)(米).
依题意得:x(270﹣3x)=6075,
2
整理得:x ﹣90x+2025=0,
解得:x1=x2=45.
答:AE 的长为 45 米.…………………………………………………………6分
19.解:(1)小亮说的对
理由:在△ABD 中,∠ABD=90°,∠BAD=18°,BA=10m,
BD
∵tan∠BAD= ,
BA
∴BD=10×tan18°,
∴CD=BD﹣BC=10×tan18°﹣0.5≈2.75(m).…………………………3 分
在△ABD 中,∠CDE=90°﹣∠BAD=72°,∠ECD=18°
∵CE⊥ED,
CE
∴cos∠ECD= ,
CD
∴CE=cos∠ECD×CD=cos18°×2.75≈2.6(m),
∵2.6m<2.7m,且 CE⊥AE,
∴小亮说的对;………………………………………………………………7 分
1
20.解:(1)当 y=0 时, x+2=0,
2
解得:x=﹣4,
∴点 A 的坐标为(﹣4,0);
1
当 x=0 时,y= x+2=2,
2
∴点 C 的坐标为(0,2);
7
ì
b 1 = a + 2
2
设点 P 的坐标为(a,b)(a>0),则 í ,
1
(a +4)×b = 9 2
ìa = 2 ì a = -10
解得: í 1 í 2, (舍去),
b1 = 3 b2 = -3
∴点 P 的坐标为(2,3).
故答案为:(﹣4,0);(0,2);(2,3).………………………………3 分
(2)如图 1,作点 Q 关于 x 轴的对称点 Q′,连接 PQ′与 x 轴交于点 M,连接 QM,此时
△PQM 的周长最小.
k
∵点 P(2,3)在反比例函数 y= 图象上,
x
6
∴k=2×3=6,即反比例函数解析式为 y=
x
∴点 Q 的坐标为(6,1),点 Q′的坐标为(6,﹣1).
设直线 PQ′的解析式为 y=mx+n(m≠0),
ì2m +n = 3
将 P(2,3),Q(6,﹣1)代入 y=mx+n,得: í ,
6m +n = -1
ì m = -1
解得: í ,
n = 5
∴直线 PQ′的解析式为 y=﹣x+5.
当 y=0 时,﹣x+5=0,
解得:x=5,
∴点 M 的坐标为(5,0),
∴当△PQM 的周长最小时,点 M 的坐标为(5,0).…………………………7 分
21.解:(1)15÷30%=50(人),
所以,参加问卷调查的学生人数为 50 名,…………………………2 分
8
参加“剪纸”课程的人数为:50-15-10-5=20(名)
画图并标注相应数据,如下图所示.
………………………………………4 分
故答案为:50;
(2)5÷50=0.1=10%
故答案为 10;…………………………………………………7 分
10
(3)由题意得:1000 200(名).
50
答:选择“刺绣”课程有 200 名学生.……………………10 分
22.证明:(1) DC 是 O 的切线,
OCD 90 ,
D 30 ,
BOC D OCD 30 90 120 ,……………………………………2 分
OB OC ,
B OCB 30 ,
DCB 120 BOC ,
又 B D 30 ,
BOC∽ BCD ;…………………………………………………………5 分
(2) D 30 , DC 3, OCD 90 ,
DC 3OC 3,DO 2OC,
OC 1 OB, DO 2,
9
B D 30 ,
DC BC 3,
BCD的周长 CD BC DB 3 3 2 1 3 2 3 .………………10 分
23.解:(1)如图, △BFE由 BCE折叠得到,
BE CF ,
ECF BEC 90 .
又 四边形 ABCD 是正方形,
D BCE 90 ,
ECF CGD 90 ,
BEC CGD,
又 正方形 ABCD
BC CD,,
△BCE≌△CDG(AAS).……………………………………………………4 分
(2)如图,连接 EH ,
由(1)得△BCE ≌△CDG,
CE DG 9,
由折叠得 BC BF ,CE FE 9,
BCF BFC.
四边形 ABCD是正方形,
AD//BC,
BCG HGF ,
又 BFC HFG,
HFG HGF,
HF HG.
10
HD 4 ,DG 9,
HF 5
HD 4,HF HG 5.…………………………………………………7 分
D HFE 90
HF 2 FE2 DH 2 DE2,
52 92 42 DE2,
DE 3 10 (DE 3 10舍去).……………………………………10 分
1
24.解:(1)把 A(-1,0),B(4,0)代入 y x2 bx c,得
2
1
b c
3
0 b
2 ,解得: 2,
8 4b c 0 c 2
1 3
∴抛物线的解析式是 y x 2 x 2;…………………………………3 分
2 2
(2)令 x=0,则 y=2,即 C(0,2),
∵ AC 2 12 22 5, BC 2 22 42 20 2,AB =25,
∴ AC 2 BC 2 AB2 ,
∴∠ACB=90°,
∵∠ACO+∠CAO=∠CBA+∠CAO=90°,
∴∠ACO=∠CBA,………………………………………………………………5 分
在 x 轴上取点 E(2,0),连接 CE,如图,
则 CO=OE=2,
∴∠OCE=45°,
∴∠ACE=∠ACO+45°=∠CBA+45°=∠CAQ,
∴CE∥PQ,
∵C(0,2),E(2,0),
∴直线 CE 的解析式为 y=-x+2,………………………………………………7分
11
设直线 PQ 的解析式为 y=-x+n,把点 A(-1,0)代入,可得 n=-1,
∴直线 PQ 的解析式为 y=-x-1,
y
1
x2 3 x 2 x 1 x 6
解方程组 2 2 ,得 或 ,
y x 1
y 0 y 7
∴点 P 的坐标是(6,-7);………………………………………………10 分
12
九年级数学试题
(满分 120 分,时间:120 分钟)
一、选择题:本大题共 8 个小题,每小题 3 分,共 24 分,在每小题给出的四个选项 A、B、C、
D 中,只有一项是正确的,请把正确的选项填在答题卡的相应位置
1.在疫情防控的特殊时期,为了满足初三高三学生的复习备考需求,菏泽市教委联合菏泽卫
视共同推出电视课堂节目:“空中课堂”,在节目播出期间.全市约有 200000 名师生收看
了节目.将 200000 用科学记数法表示应为
5 6 5 6
A.0.2×10 B.0.2×10 C.2×10 D.2×10
2.下列图形中,是轴对称图形的是
A. B. C. D.
3.A、B 是数轴上位于原点 O 异侧的两点(点 A 在点 B 的左侧),若点 A、B 分别对应的实数
为 a、b,且|a|>|b|,则 a、-a、b、-b 中最大的数是
A.a B.-a C.b D. -b
4.如图,该立体图形的俯视图是
A. B. C. D.
第 5题图
5. 如图,三角板的直角顶点落在矩形纸片的一边上.若
∠1=35°,则∠2 的度数是
A.35° B.55° C.45° D.65°
2 a 1 a6.如果 a a 1 0,那么代数式 1 2 的值是 a 2a 1 a 1
第 7 题图
A. 3 B. 1 C. -1 D. -3
7.小明收集了鄂尔多斯市某酒店 2022 年 3 月 1 日~3 月 6 日每天的用水量(单位:吨),整
理并绘制成如图所示的折线统计图,下列结论正确的是
23 25
A.平均数是 B.众数是 10 C.中位数是 8.5 D.方差是
4 3
8.如图,在平面直角坐标系中,菱形ABCD 在第一象限内,
边BC 与x 轴平行,A、B 两点的纵坐标分别为4、1,反比例
函数 y k= 的图象经过 A、B 两点,菱形ABCD 的面积为9 2 , 第 8 题图
x
1
则k 的值为
A.4 B.5 C.6 D.9
二、填空题(本大题共 6个小题,每小题 3 分,共 18 分,只要求
三、把最后的结果填写在答题卡的相应区域内)
9.因式分解:4a2b-b ;
10.如图 A'B'∥AB,B'C'∥BC,且 OA':A'A=4:3,则△ABC 与△A'B'C'是位似图形,△ABC 与△A'B'C'
的位似比为 ;
第13题图 第 14 题图第 10 题图
11.若 a、b、c 的方差为 3,则 2a+3、2b+3、2c+3 的方差为_ ;
12.设 m,n 是方程 x2-2x-2022=0 的两个实数根,则 m2-m+n 的值为_____;
13.如图,正方形 ABCD 中,扇形 ABC 与扇形 BCD 的弧交于点 E,AB=2cm,则图中阴影部分的
面积为 cm2;(不求近似值)
2
14.如图,若二次函数 y=ax +bx+c(a≠0)的图象的对称轴为直线 x=1,与 y 轴交于点 C,与
x轴交于点 A、点 B(-1,0),则下列结论:①abc>0; ②二次函数的最大值为 a+b+c;
2
③a-b+c<0;④b -4ac<0;⑤当 y>0 时,-1
0.04 +cos2 45O -1 115.(6 分) 计算: - 2 + | - |
2
2 3 x -3 x +6
16.(6 分)已知 x +3x-3=0,求代数式(1- ) - 的值.
x x +3 x +3
0
17.(6 分) 如图,在 Rt△ABC 中,∠C=90 ,AB 的垂直平分线交 AC 于 第17题图
点 D,交 AB 于点 E.(1)求证:△ADE∽△ABC;(2)当 AC=8,BC=6 时,求 DE 的长.
18.(6 分)为了更好的收治新冠肺炎患者,某市计划用 810 米的建筑材料在一个空地上搭建方
舱医院,如图所示是医院的平面图,医院分为三个区,矩形 BFHG 区用于隔离治疗重症患者,
矩形 CDEF 区用于隔离治疗轻症患者,医护室是正方形 AGHE,已知围成轻症患者区的建筑材
料与围成医护室、重症患者区的建筑材料之和一样多,设 AE=x 米.
(1)用含 x 的代数式表示:DE= 米,AB= 米;
(2)设矩形 BFHG 的面积为 6075 平方米,求 AE 的长.
第18题图
2
19.(7 分)郓城县为缓解“停车难”问题,建造地下停车库,如图,已知 AB⊥BD,∠BAD=18°,
C 在 BD 上,BC=0.5m.根据规定,停车库坡道入口上方要张贴限高标准值,以告知驾驶
员能否安全驶入.小明认为 CD 的长就是限高值,而小亮认为应该以 CE 的长作为限高
值.(参考数据:sin18°≈0.31,cos18°≈0.95,tan18°≈0.325,结果精确到 0.1m)
请你判断小明和小亮谁说的对?并说明理由;
第 19 题图
第 20 题图 第 21 题图
1
20.(7 分)如图,已知一次函数 y= x+2 的图象分别与 x 轴、y 轴交于点 A、C,与反比例函
2
k
数 y= 的图象在第一象限内交于点 P,过点 P作 PB⊥x 轴,垂足为 B,且△ABP 的面积为 9.
x
(1)点 A 的坐标为 ,点 C的坐标为 ,点 P 的坐标为 ;
k
(2)已知点 Q 在反比例函数 y= 的图象上,其横坐标为 6,在 x 轴上确定一点 M,使得△
x
PQM 的周长最小,求出点 M 的坐标;
21.(10 分)某学校计划在八年级开设“折扇”、“刺绣”、“剪纸”、“陶艺”四门校本
课程,要求每人必须参加,并且只能选择其中一门课程.为了解学生对这四门课程的选择情
况,学校从八年级全体学生中随机抽取部分学生进行问卷调查.并根据调查结果绘制成如图
所示的条形统计图和扇形统计图(部分信息未给出).
请你根据以上信息解决下列问题:
(1)参加问卷调查的学生人数为______名.补全条形统计图(画图并标注相应数据);
(2)在扇形统计图中,选择“陶艺”课程的学生占______%;
(3)若该校八年级一共有 1000 名学生,试估计选择“刺绣”课程的学生有多少名?
3
22.(10 分) 如图,DB 过 O 的圆心,交 O 于点 A、B,DC 是 O 的切线,点 C 是切点,
0
已知∠D=30 ,DC= 3.(1)求证:△BOC∽△BCD;(2)求△BCD 的周长.
第 22 题图
23.(10 分)如图 1,在正方形 ABCD 中,点 E 是 CD 上一动点,将正方形沿着 BE 折叠,点 C
落在点 F 处,连结 BE,CF,延长 CF 交 AD 于点 G.
(1)求证:△BCE≌△CDG.
HD 4
(2)如图 2,在(1)的条件下,延长 BF 交 AD 于点 H.若 ,CE=9,求线段 DE 的长.
HF 5
第23题图
1 2
24.(10 分)如图,抛物线 y=- x +bx+c 与 x 轴交于 A(-1,0),B(4,0),与 y 轴交于点 C.连
2
接 AC,BC,点 P 在抛物线上运动.
(1)求抛物线的表达式;
(2)若点 P 在第四象限,点 Q 在 PA 的延长线上,
当∠CAQ=∠CBA 45°时,求点 P 的坐标; 第24题图
4
2021——2022 学年度第二学期期中教学质量检测
九年级数学试题参考答案
一、选择题答题栏(每小题选对得 3 分,共 24 分)
题号 1 2 3 4 5 6 7 8
答案 C D B C B A D A
二、填空题:(每小题选对得 3 分,共 18 分)
9. b(2a+1)(2a-1) 10. 7:4 11. 12 12.2024 13. 14.②⑤⑥
3
三、解答题:本大题共 10 小题,共 78 分.解答要写出必要的文字说明、证明过程或演算步
骤
2 0 -1 1
15.(6 分)解: 0.04 +cos 45 - 2 + | - |
2
2 1 1
=0.2+( )2 - + …………………………………………………4 分
2 2 2
1 1 1
=0.2+ - +
2 2 2
=0.7……………………………………………………………………6 分
3 x -3 x +6
16.(6 分)解:(1- ) -
x x +3 x +3
x - 3 x - 3 x +6
= - …………………………………………………………1 分
x x +3 x +3
x - 3 x+3 x +6
= -
x x - 3 x +3
x+3 x +6
= - …………………………………………………………………3 分
x x +3
(x+3)2 - x(x +6)
=
(x x+3)
9
= 2 ………………………………………………………………………4 分x +3x
2
∵x +3x-3=0
2
∴x +3x=3………………………………………………………………………5 分
5
9
则原式= 2 =3………………………………………………………………6 分x +3x
17.(6 分)证明:(1) ∵DE垂直平分 AB ,
∴ AED 90 .
∴ AED C .
∵ A A,
∴△ADE∽△ABC…………………………………………………………3 分
(2) Rt△ABC中, AC 8, BC 6,
∴ AB 10.
∵DE平分 AB,
∴ AE 5.
∵△ADE∽△ABC,
DE AE
∴ .
BC AC
DE 5
∴ .
6 8
DE 15∴ ………………………………………………………………6 分
4
18.(6 分)解:(1)∵四边形 ABCD 为矩形,
∴AB=CD,
∵围成轻症患者区的建筑材料与围成医护室、重症患者区的建筑材料之和一样多,
∴AE+GH+BF=DE+CF,
即 3AE=2DE.
3
设 AE=x 米,则 DE= x 米.
2
∵搭建方舱医院的材料总长度为 810 米,
810 -3AE - 2DE 810 -3x - 2
3
x
∴AB= = 2 (270﹣2x)米.
3 3
3
故答案为: x米;(270﹣2x)米.………………………………………2 分
2
(2)∵四边形 AGHE 为正方形,
6
∴AG=AE=x 米,
∴BG=AB﹣AG=270﹣2x﹣x=(270﹣3x)(米).
依题意得:x(270﹣3x)=6075,
2
整理得:x ﹣90x+2025=0,
解得:x1=x2=45.
答:AE 的长为 45 米.…………………………………………………………6分
19.解:(1)小亮说的对
理由:在△ABD 中,∠ABD=90°,∠BAD=18°,BA=10m,
BD
∵tan∠BAD= ,
BA
∴BD=10×tan18°,
∴CD=BD﹣BC=10×tan18°﹣0.5≈2.75(m).…………………………3 分
在△ABD 中,∠CDE=90°﹣∠BAD=72°,∠ECD=18°
∵CE⊥ED,
CE
∴cos∠ECD= ,
CD
∴CE=cos∠ECD×CD=cos18°×2.75≈2.6(m),
∵2.6m<2.7m,且 CE⊥AE,
∴小亮说的对;………………………………………………………………7 分
1
20.解:(1)当 y=0 时, x+2=0,
2
解得:x=﹣4,
∴点 A 的坐标为(﹣4,0);
1
当 x=0 时,y= x+2=2,
2
∴点 C 的坐标为(0,2);
7
ì
b 1 = a + 2
2
设点 P 的坐标为(a,b)(a>0),则 í ,
1
(a +4)×b = 9 2
ìa = 2 ì a = -10
解得: í 1 í 2, (舍去),
b1 = 3 b2 = -3
∴点 P 的坐标为(2,3).
故答案为:(﹣4,0);(0,2);(2,3).………………………………3 分
(2)如图 1,作点 Q 关于 x 轴的对称点 Q′,连接 PQ′与 x 轴交于点 M,连接 QM,此时
△PQM 的周长最小.
k
∵点 P(2,3)在反比例函数 y= 图象上,
x
6
∴k=2×3=6,即反比例函数解析式为 y=
x
∴点 Q 的坐标为(6,1),点 Q′的坐标为(6,﹣1).
设直线 PQ′的解析式为 y=mx+n(m≠0),
ì2m +n = 3
将 P(2,3),Q(6,﹣1)代入 y=mx+n,得: í ,
6m +n = -1
ì m = -1
解得: í ,
n = 5
∴直线 PQ′的解析式为 y=﹣x+5.
当 y=0 时,﹣x+5=0,
解得:x=5,
∴点 M 的坐标为(5,0),
∴当△PQM 的周长最小时,点 M 的坐标为(5,0).…………………………7 分
21.解:(1)15÷30%=50(人),
所以,参加问卷调查的学生人数为 50 名,…………………………2 分
8
参加“剪纸”课程的人数为:50-15-10-5=20(名)
画图并标注相应数据,如下图所示.
………………………………………4 分
故答案为:50;
(2)5÷50=0.1=10%
故答案为 10;…………………………………………………7 分
10
(3)由题意得:1000 200(名).
50
答:选择“刺绣”课程有 200 名学生.……………………10 分
22.证明:(1) DC 是 O 的切线,
OCD 90 ,
D 30 ,
BOC D OCD 30 90 120 ,……………………………………2 分
OB OC ,
B OCB 30 ,
DCB 120 BOC ,
又 B D 30 ,
BOC∽ BCD ;…………………………………………………………5 分
(2) D 30 , DC 3, OCD 90 ,
DC 3OC 3,DO 2OC,
OC 1 OB, DO 2,
9
B D 30 ,
DC BC 3,
BCD的周长 CD BC DB 3 3 2 1 3 2 3 .………………10 分
23.解:(1)如图, △BFE由 BCE折叠得到,
BE CF ,
ECF BEC 90 .
又 四边形 ABCD 是正方形,
D BCE 90 ,
ECF CGD 90 ,
BEC CGD,
又 正方形 ABCD
BC CD,,
△BCE≌△CDG(AAS).……………………………………………………4 分
(2)如图,连接 EH ,
由(1)得△BCE ≌△CDG,
CE DG 9,
由折叠得 BC BF ,CE FE 9,
BCF BFC.
四边形 ABCD是正方形,
AD//BC,
BCG HGF ,
又 BFC HFG,
HFG HGF,
HF HG.
10
HD 4 ,DG 9,
HF 5
HD 4,HF HG 5.…………………………………………………7 分
D HFE 90
HF 2 FE2 DH 2 DE2,
52 92 42 DE2,
DE 3 10 (DE 3 10舍去).……………………………………10 分
1
24.解:(1)把 A(-1,0),B(4,0)代入 y x2 bx c,得
2
1
b c
3
0 b
2 ,解得: 2,
8 4b c 0 c 2
1 3
∴抛物线的解析式是 y x 2 x 2;…………………………………3 分
2 2
(2)令 x=0,则 y=2,即 C(0,2),
∵ AC 2 12 22 5, BC 2 22 42 20 2,AB =25,
∴ AC 2 BC 2 AB2 ,
∴∠ACB=90°,
∵∠ACO+∠CAO=∠CBA+∠CAO=90°,
∴∠ACO=∠CBA,………………………………………………………………5 分
在 x 轴上取点 E(2,0),连接 CE,如图,
则 CO=OE=2,
∴∠OCE=45°,
∴∠ACE=∠ACO+45°=∠CBA+45°=∠CAQ,
∴CE∥PQ,
∵C(0,2),E(2,0),
∴直线 CE 的解析式为 y=-x+2,………………………………………………7分
11
设直线 PQ 的解析式为 y=-x+n,把点 A(-1,0)代入,可得 n=-1,
∴直线 PQ 的解析式为 y=-x-1,
y
1
x2 3 x 2 x 1 x 6
解方程组 2 2 ,得 或 ,
y x 1
y 0 y 7
∴点 P 的坐标是(6,-7);………………………………………………10 分
12
同课章节目录
