3.2.2 双曲线的简单几何性质(1) 导学案
文档属性
| 名称 | 3.2.2 双曲线的简单几何性质(1) 导学案 | 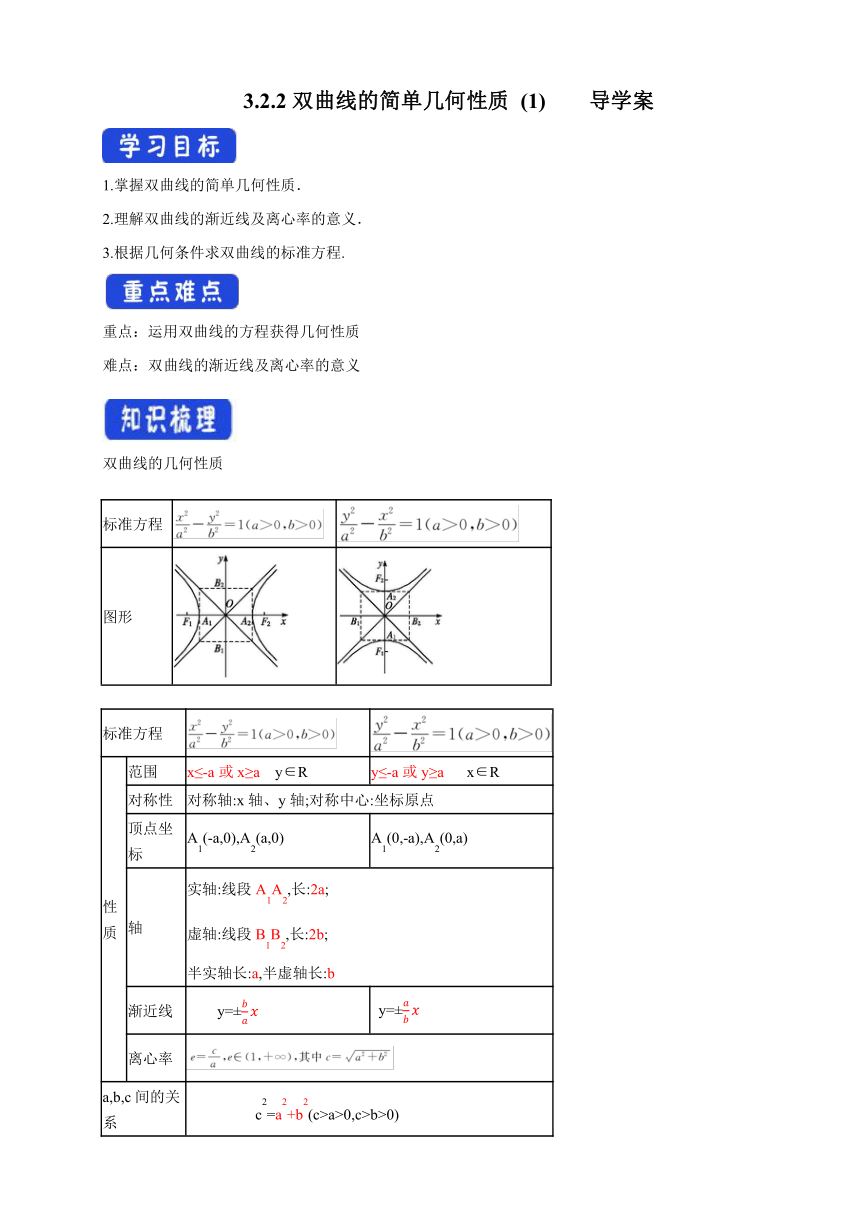 | |
| 格式 | docx | ||
| 文件大小 | 484.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-29 21:52:26 | ||
图片预览




文档简介
3.2.2双曲线的简单几何性质 (1) 导学案
1.掌握双曲线的简单几何性质.
2.理解双曲线的渐近线及离心率的意义.
3.根据几何条件求双曲线的标准方程.
重点:运用双曲线的方程获得几何性质
难点:双曲线的渐近线及离心率的意义
双曲线的几何性质
标准方程
图形
标准方程
性 质 范围 x≤-a或x≥a y∈R y≤-a或y≥a x∈R
对称性 对称轴:x轴、y轴;对称中心:坐标原点
顶点坐标 A1(-a,0),A2(a,0) A1(0,-a),A2(0,a)
轴 实轴:线段A1A2,长:2a; 虚轴:线段B1B2,长:2b; 半实轴长:a,半虚轴长:b
渐近线 y=± y=±
离心率
a,b,c间的关系 c2=a2+b2(c>a>0,c>b>0)
(1)双曲线与椭圆的六个不同点:
双曲线 椭圆
曲线 两支曲线 封闭的曲线
顶点 两个顶点 四个顶点
轴 实、虚轴 长、短轴
渐近线 有渐近线 无渐近线
离心率 e>1 0a,b,c关系 a2+b2=c2 a2-b2=c2
(2)等轴双曲线是实轴和虚轴等长的双曲线,它的渐近线方程是y=±x,离心率为 .
(3)共轭双曲线:以已知双曲线的虚轴为实轴,实轴为虚轴的双曲线叫做原双曲线的共轭双曲线.
1.判断
(1)双曲线=1与=1(a>0,b>0)的形状相同. ( )
(2)双曲线=1与=1(a>0,b>0)的渐近线相同. ( )
(3)等轴双曲线的渐近线互相垂直. ( )
2.圆锥曲线=1的离心率e=2,则实数m的值为( )
A.-5 B.-35 C.19 D.-11
问题导学
类比椭圆几何性质的研究,你认为应该研究双曲线
(>0,>0),的哪些几何性质,如何研究这些性质?
1、范围
利用双曲线的方程求出它的范围,由方程可得
于是,双曲线上点的坐标( , )都适合不等式,
所以 或;
2、对称性
(>0,>0),关于x轴、y轴和原点都是对称。
x轴、y轴是双曲线的对称轴,原点是对称中心,
又叫做双曲线的中心。
3、顶点
(1)双曲线与对称轴的交点,叫做双曲线的顶点 .
顶点是
(2)如图,线段 叫做双曲线的实轴,它的长为2a,a叫做实半轴长;线段 叫做双曲线的虚轴,它的长为2b,b叫做双曲线的虚半轴长。
(3)实轴与虚轴等长的双曲线叫等轴双曲线
4、渐近线
(1)双曲线 (>0,>0),的渐近线方程为:
(2)利用渐近线可以较准确的画出双曲线的草图
4、渐近线
慢慢靠近
5、离心率
(1)定义:e =
(2)e的范围:e >1
(3)e的含义:因为另外,
注意到=;说明越趋近于1,则的值越小,
因此双曲线的渐近线所夹得双曲线区域越狭窄.
如果双曲线C的标准方程是
(>0,>0),
那么该双曲线的范围、对称性、顶点、渐近线、离心率中,
那些与焦点在轴上的双曲线是有区别的?
典例解析
例1 求双曲线9y2-4x2=-36的顶点坐标、焦点坐标、实轴长、虚轴长、离心率、
渐近线方程.
由双曲线的方程研究其几何性质的注意点
(1)把双曲线方程化为标准形式是解决此类题的关键.
(2)由标准方程确定焦点位置,确定a,b的值.
(3)由c2=a2+b2求出c的值,从而写出双曲线的几何性质.
跟踪训练1 求双曲线nx2-my2=mn(m>0,n>0)的半实轴长、半虚轴长、焦点坐标、离心率、顶点坐标和渐近线方程.
例2 根据以下条件,求双曲线的标准方程.
(1)过点P(3,-),离心率为;
(2)与椭圆=1有公共焦点,且离心率e=;
(3)与双曲线=1有共同渐近线,且过点(-3,2).
2.巧设双曲线方程的六种方法与技巧
(1)焦点在x轴上的双曲线的标准方程可设为=1(a>0,b>0).
(2)焦点在y轴上的双曲线的标准方程可设为=1(a>0,b>0).
(3)与双曲线=1共焦点的双曲线方程可设为=1(λ≠0,-b2<λ(4)与双曲线=1具有相同渐近线的双曲线方程可设为=λ(λ≠0).
(5)渐近线为y=±kx的双曲线方程可设为k2x2-y2=λ(λ≠0).
(6)渐近线为ax±by=0的双曲线方程可设为a2x2-b2y2=λ(λ≠0).
跟踪训练2 求适合下列条件的双曲线的标准方程.
(1)焦点在x轴上,虚轴长为8,离心率为;
(2)过点(2,0),与双曲线=1离心率相等.
1.双曲线mx2+y2=1的虚轴长是实轴长的2倍,则m的值为( )
A.4 B.-4 C.- D.
2.(多选)若双曲线C的一个焦点F(5,0),P是双曲线上一点,且渐近线方程为y=±x,则下列结论正确的是 ( )
A.C的方程为=1
B.C的离心率为
C.焦点到渐近线的距离为3
D.|PF|的最小值为2
3.中心在原点,焦点在x轴上,且一个焦点在直线3x-4y+12=0上的等轴双曲线的方程是 .
4.关于双曲线=-1,有以下说法:
①实轴长为6;②双曲线的离心率是;③焦点坐标为(±5,0);④渐近线方程是y=±x;⑤焦点到渐近线的距离等于3.
正确的说法是 .(把所有正确说法的序号都填上)
5.已知F为双曲线C:=1的左焦点,P,Q为双曲线C同一支上的两点.若PQ的长等于虚轴长的2倍,点A(,0)在线段PQ上,则△PQF的周长为 .
参考答案:
知识梳理
1.答案:(1)√ (2)× (3)√
2.解析:由圆锥曲线=1的离心率e=2,说明曲线是双曲线,
所以m<-8,∴e==2,解得m=-35.
答案:B
学习过程
二、典例解析
例1 解:将9y2-4x2=-36化为标准方程为=1,
即=1,所以a=3,b=2,c=.
因此顶点坐标为(-3,0),(3,0),
焦点坐标为(-,0),(,0),
实轴长2a=6,虚轴长2b=4,
离心率e=,
渐近线方程为y=±x=±x.
跟踪训练1 解:把方程nx2-my2=mn(m>0,n>0)
化为标准方程为=1(m>0,n>0),
由此可知,半实轴长a=,
半虚轴长b=,c=,
焦点坐标为(,0),(-,0),
离心率e=,
顶点坐标为(-,0),(,0),
所以渐近线方程为y=± x,即y=±x.
例2 解:(1)若双曲线的焦点在x轴上,设其方程为=1(a>0,b>0),
∵e=,∴=2,即a2=b2. ①
又双曲线过P(3,-),∴=1, ②
由①②得a2=b2=4,故双曲线方程为=1.
若双曲线的焦点在y轴上,
设其方程为=1(a>0,b>0),
同理有a2=b2, ③
=1, ④
由③④得a2=b2=-4(舍去).综上,双曲线的标准方程为=1.
(2)由椭圆方程=1,知半焦距为,
∴焦点是F1(-,0),F2(,0).
因此双曲线的焦点为(-,0),(,0).
设双曲线方程为=1(a>0,b>0),
由已知条件,有解得
∴所求双曲线的标准方程为-y2=1.
(3)设所求双曲线方程为=λ(λ≠0),
将点(-3,2)代入得λ=,
∴双曲线方程为,
即双曲线的标准方程为=1.
跟踪训练2 解:(1)设所求双曲线的标准方程为=1(a>0,b>0),由题意知2b=8,e=,
从而b=4,c=a,
代入c2=a2+b2,得a2=9,
故双曲线的标准方程为=1.
(2)由题意知,所求双曲线的焦点在x轴上,
故可设其方程为=λ(λ>0),
将点(2,0)的坐标代入方程得λ=,
故所求双曲线的标准方程为-y2=1.
达标检测
1.解析:由双曲线方程mx2+y2=1,知m<0,
则双曲线方程可化为y2-=1,
则a2=1,a=1,又虚轴长是实轴长的2倍,
∴b=2,∴-=b2=4,∴m=-,故选C.
答案:C
2.(多选)解析:双曲线C的一个焦点F(5,0),且渐近线方程为y=±x,可得c=5,焦点坐标在x轴上,
所以,因为c=5,所以b=4,a=3,
所以C的方程为=1,A正确;
离心率为e=,B不正确;
焦点到渐近线的距离为d==4,C不正确;
|PF|的最小值为c-a=2,D正确.
答案:AD
3.解析:令y=0,得x=-4,
∴等轴双曲线的一个焦点为(-4,0),
∴c=4,a2=b2=c2=×16=8,故等轴双曲线的方程为x2-y2=8.
答案:x2-y2=8
4.解析:∵双曲线=-1,
即=1,∴a=4,b=3,c==5,
∴①实轴长为2a=8,故①错误;
②双曲线的离心率是e=,故②正确;
③焦点坐标为F(0,±5),故③错误;
④渐近线方程是y=±x,故④正确;
⑤焦点到渐近线的距离为d==3,故⑤正确.
答案:②④⑤
5.解析:根据题意,双曲线C:=1的左焦点F(-,0),所以点A(,0)是双曲线的右焦点,P,Q为双曲线C右支上的两点.虚轴长为6,所以|PQ|=12.
双曲线图像如图.
|PF|-|AP|=2a=4,①
|QF|-|QA|=2a=4,②
①+②得|PF|+|QF|-|PQ|=8,
∴周长为|PF|+|QF|+|PQ|=8+2|PQ|=32.
答案:32
1.掌握双曲线的简单几何性质.
2.理解双曲线的渐近线及离心率的意义.
3.根据几何条件求双曲线的标准方程.
重点:运用双曲线的方程获得几何性质
难点:双曲线的渐近线及离心率的意义
双曲线的几何性质
标准方程
图形
标准方程
性 质 范围 x≤-a或x≥a y∈R y≤-a或y≥a x∈R
对称性 对称轴:x轴、y轴;对称中心:坐标原点
顶点坐标 A1(-a,0),A2(a,0) A1(0,-a),A2(0,a)
轴 实轴:线段A1A2,长:2a; 虚轴:线段B1B2,长:2b; 半实轴长:a,半虚轴长:b
渐近线 y=± y=±
离心率
a,b,c间的关系 c2=a2+b2(c>a>0,c>b>0)
(1)双曲线与椭圆的六个不同点:
双曲线 椭圆
曲线 两支曲线 封闭的曲线
顶点 两个顶点 四个顶点
轴 实、虚轴 长、短轴
渐近线 有渐近线 无渐近线
离心率 e>1 0
(2)等轴双曲线是实轴和虚轴等长的双曲线,它的渐近线方程是y=±x,离心率为 .
(3)共轭双曲线:以已知双曲线的虚轴为实轴,实轴为虚轴的双曲线叫做原双曲线的共轭双曲线.
1.判断
(1)双曲线=1与=1(a>0,b>0)的形状相同. ( )
(2)双曲线=1与=1(a>0,b>0)的渐近线相同. ( )
(3)等轴双曲线的渐近线互相垂直. ( )
2.圆锥曲线=1的离心率e=2,则实数m的值为( )
A.-5 B.-35 C.19 D.-11
问题导学
类比椭圆几何性质的研究,你认为应该研究双曲线
(>0,>0),的哪些几何性质,如何研究这些性质?
1、范围
利用双曲线的方程求出它的范围,由方程可得
于是,双曲线上点的坐标( , )都适合不等式,
所以 或;
2、对称性
(>0,>0),关于x轴、y轴和原点都是对称。
x轴、y轴是双曲线的对称轴,原点是对称中心,
又叫做双曲线的中心。
3、顶点
(1)双曲线与对称轴的交点,叫做双曲线的顶点 .
顶点是
(2)如图,线段 叫做双曲线的实轴,它的长为2a,a叫做实半轴长;线段 叫做双曲线的虚轴,它的长为2b,b叫做双曲线的虚半轴长。
(3)实轴与虚轴等长的双曲线叫等轴双曲线
4、渐近线
(1)双曲线 (>0,>0),的渐近线方程为:
(2)利用渐近线可以较准确的画出双曲线的草图
4、渐近线
慢慢靠近
5、离心率
(1)定义:e =
(2)e的范围:e >1
(3)e的含义:因为另外,
注意到=;说明越趋近于1,则的值越小,
因此双曲线的渐近线所夹得双曲线区域越狭窄.
如果双曲线C的标准方程是
(>0,>0),
那么该双曲线的范围、对称性、顶点、渐近线、离心率中,
那些与焦点在轴上的双曲线是有区别的?
典例解析
例1 求双曲线9y2-4x2=-36的顶点坐标、焦点坐标、实轴长、虚轴长、离心率、
渐近线方程.
由双曲线的方程研究其几何性质的注意点
(1)把双曲线方程化为标准形式是解决此类题的关键.
(2)由标准方程确定焦点位置,确定a,b的值.
(3)由c2=a2+b2求出c的值,从而写出双曲线的几何性质.
跟踪训练1 求双曲线nx2-my2=mn(m>0,n>0)的半实轴长、半虚轴长、焦点坐标、离心率、顶点坐标和渐近线方程.
例2 根据以下条件,求双曲线的标准方程.
(1)过点P(3,-),离心率为;
(2)与椭圆=1有公共焦点,且离心率e=;
(3)与双曲线=1有共同渐近线,且过点(-3,2).
2.巧设双曲线方程的六种方法与技巧
(1)焦点在x轴上的双曲线的标准方程可设为=1(a>0,b>0).
(2)焦点在y轴上的双曲线的标准方程可设为=1(a>0,b>0).
(3)与双曲线=1共焦点的双曲线方程可设为=1(λ≠0,-b2<λ
(5)渐近线为y=±kx的双曲线方程可设为k2x2-y2=λ(λ≠0).
(6)渐近线为ax±by=0的双曲线方程可设为a2x2-b2y2=λ(λ≠0).
跟踪训练2 求适合下列条件的双曲线的标准方程.
(1)焦点在x轴上,虚轴长为8,离心率为;
(2)过点(2,0),与双曲线=1离心率相等.
1.双曲线mx2+y2=1的虚轴长是实轴长的2倍,则m的值为( )
A.4 B.-4 C.- D.
2.(多选)若双曲线C的一个焦点F(5,0),P是双曲线上一点,且渐近线方程为y=±x,则下列结论正确的是 ( )
A.C的方程为=1
B.C的离心率为
C.焦点到渐近线的距离为3
D.|PF|的最小值为2
3.中心在原点,焦点在x轴上,且一个焦点在直线3x-4y+12=0上的等轴双曲线的方程是 .
4.关于双曲线=-1,有以下说法:
①实轴长为6;②双曲线的离心率是;③焦点坐标为(±5,0);④渐近线方程是y=±x;⑤焦点到渐近线的距离等于3.
正确的说法是 .(把所有正确说法的序号都填上)
5.已知F为双曲线C:=1的左焦点,P,Q为双曲线C同一支上的两点.若PQ的长等于虚轴长的2倍,点A(,0)在线段PQ上,则△PQF的周长为 .
参考答案:
知识梳理
1.答案:(1)√ (2)× (3)√
2.解析:由圆锥曲线=1的离心率e=2,说明曲线是双曲线,
所以m<-8,∴e==2,解得m=-35.
答案:B
学习过程
二、典例解析
例1 解:将9y2-4x2=-36化为标准方程为=1,
即=1,所以a=3,b=2,c=.
因此顶点坐标为(-3,0),(3,0),
焦点坐标为(-,0),(,0),
实轴长2a=6,虚轴长2b=4,
离心率e=,
渐近线方程为y=±x=±x.
跟踪训练1 解:把方程nx2-my2=mn(m>0,n>0)
化为标准方程为=1(m>0,n>0),
由此可知,半实轴长a=,
半虚轴长b=,c=,
焦点坐标为(,0),(-,0),
离心率e=,
顶点坐标为(-,0),(,0),
所以渐近线方程为y=± x,即y=±x.
例2 解:(1)若双曲线的焦点在x轴上,设其方程为=1(a>0,b>0),
∵e=,∴=2,即a2=b2. ①
又双曲线过P(3,-),∴=1, ②
由①②得a2=b2=4,故双曲线方程为=1.
若双曲线的焦点在y轴上,
设其方程为=1(a>0,b>0),
同理有a2=b2, ③
=1, ④
由③④得a2=b2=-4(舍去).综上,双曲线的标准方程为=1.
(2)由椭圆方程=1,知半焦距为,
∴焦点是F1(-,0),F2(,0).
因此双曲线的焦点为(-,0),(,0).
设双曲线方程为=1(a>0,b>0),
由已知条件,有解得
∴所求双曲线的标准方程为-y2=1.
(3)设所求双曲线方程为=λ(λ≠0),
将点(-3,2)代入得λ=,
∴双曲线方程为,
即双曲线的标准方程为=1.
跟踪训练2 解:(1)设所求双曲线的标准方程为=1(a>0,b>0),由题意知2b=8,e=,
从而b=4,c=a,
代入c2=a2+b2,得a2=9,
故双曲线的标准方程为=1.
(2)由题意知,所求双曲线的焦点在x轴上,
故可设其方程为=λ(λ>0),
将点(2,0)的坐标代入方程得λ=,
故所求双曲线的标准方程为-y2=1.
达标检测
1.解析:由双曲线方程mx2+y2=1,知m<0,
则双曲线方程可化为y2-=1,
则a2=1,a=1,又虚轴长是实轴长的2倍,
∴b=2,∴-=b2=4,∴m=-,故选C.
答案:C
2.(多选)解析:双曲线C的一个焦点F(5,0),且渐近线方程为y=±x,可得c=5,焦点坐标在x轴上,
所以,因为c=5,所以b=4,a=3,
所以C的方程为=1,A正确;
离心率为e=,B不正确;
焦点到渐近线的距离为d==4,C不正确;
|PF|的最小值为c-a=2,D正确.
答案:AD
3.解析:令y=0,得x=-4,
∴等轴双曲线的一个焦点为(-4,0),
∴c=4,a2=b2=c2=×16=8,故等轴双曲线的方程为x2-y2=8.
答案:x2-y2=8
4.解析:∵双曲线=-1,
即=1,∴a=4,b=3,c==5,
∴①实轴长为2a=8,故①错误;
②双曲线的离心率是e=,故②正确;
③焦点坐标为F(0,±5),故③错误;
④渐近线方程是y=±x,故④正确;
⑤焦点到渐近线的距离为d==3,故⑤正确.
答案:②④⑤
5.解析:根据题意,双曲线C:=1的左焦点F(-,0),所以点A(,0)是双曲线的右焦点,P,Q为双曲线C右支上的两点.虚轴长为6,所以|PQ|=12.
双曲线图像如图.
|PF|-|AP|=2a=4,①
|QF|-|QA|=2a=4,②
①+②得|PF|+|QF|-|PQ|=8,
∴周长为|PF|+|QF|+|PQ|=8+2|PQ|=32.
答案:32
