3.2.2 双曲线的简单几何性质(2) 导学案
文档属性
| 名称 | 3.2.2 双曲线的简单几何性质(2) 导学案 |
|
|
| 格式 | docx | ||
| 文件大小 | 540.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-29 21:53:35 | ||
图片预览




文档简介
3.2.2双曲线的简单几何性质 (2) 导学案
1. 掌握双曲线的简单几何性质.
2. 双曲线方程的简单应用.
3. 理解直线与双曲线的位置关系.
重点:直线与双曲线的位置关系
难点:直线与双曲线的位置关系
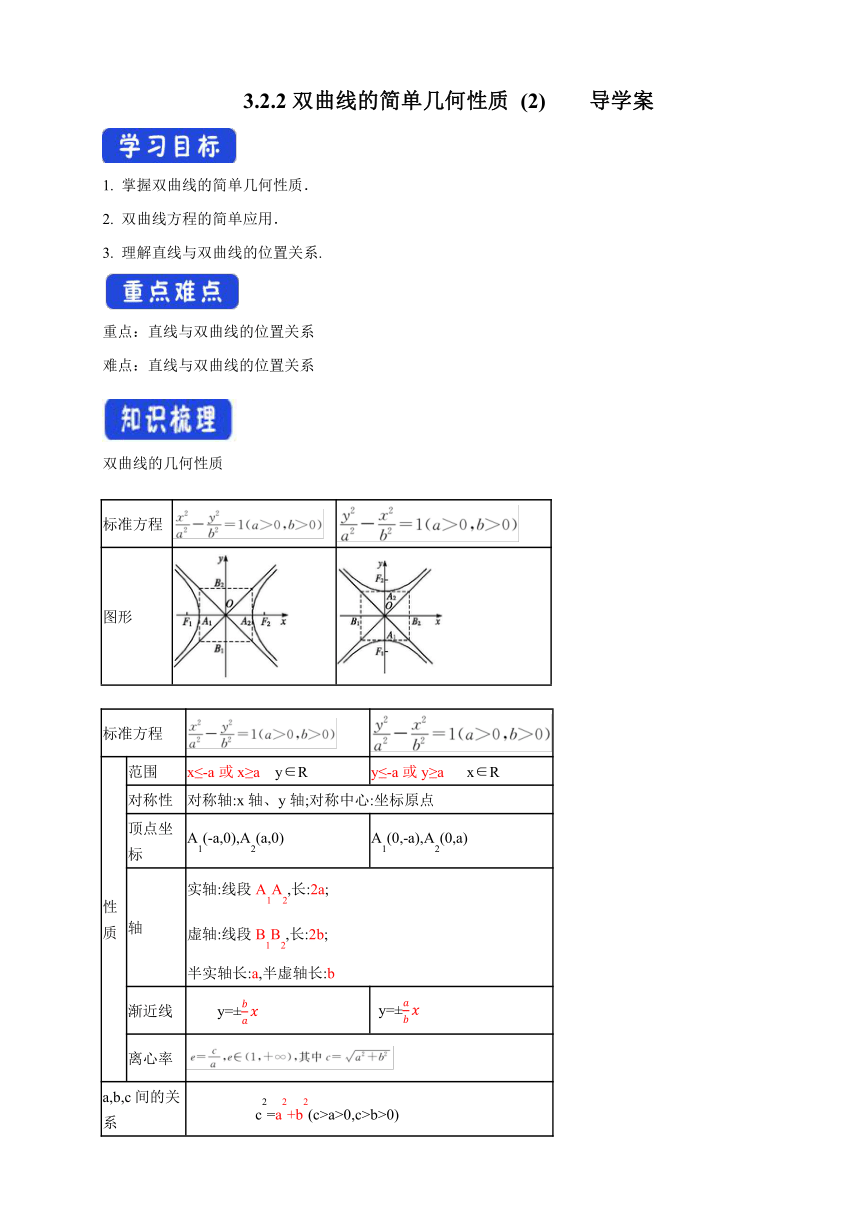
双曲线的几何性质
标准方程
图形
标准方程
性 质 范围 x≤-a或x≥a y∈R y≤-a或y≥a x∈R
对称性 对称轴:x轴、y轴;对称中心:坐标原点
顶点坐标 A1(-a,0),A2(a,0) A1(0,-a),A2(0,a)
轴 实轴:线段A1A2,长:2a; 虚轴:线段B1B2,长:2b; 半实轴长:a,半虚轴长:b
渐近线 y=± y=±
离心率
a,b,c间的关系 c2=a2+b2(c>a>0,c>b>0)
(1)双曲线与椭圆的六个不同点:
双曲线 椭圆
曲线 两支曲线 封闭的曲线
顶点 两个顶点 四个顶点
轴 实、虚轴 长、短轴
渐近线 有渐近线 无渐近线
离心率 e>1 0a,b,c关系 a2+b2=c2 a2-b2=c2
一、典例解析
例4.如图,双曲线型冷却塔的外形,是双曲线的一部分,已知塔的总高度为137.5m,塔顶直径为90m,塔的最小直径(喉部直径)为60m,喉部标高112.5m,试建立适当的坐标系,求出此双曲线的标准方程(精确到1m)
例5.已知点到定点的距离和它到定直线l:的距离的比是,则点的轨迹方程为
请你将例5与椭圆一节中的例6比较,你有什么发现?
例6、 过双曲线的右焦点F2,倾斜角为30度的直线交双曲线于A,B两点,求|AB|.
直线与双曲线位置关系的判断方法
1.方程思想的应用
把直线与双曲线的方程联立成方程组,通过消元后化为ax2+bx+c=0的形式,在a≠0的情况下考察方程的判别式.
(1)Δ>0时,直线与双曲线有两个不同的公共点.
(2)Δ=0时,直线与双曲线只有一个公共点.
(3)Δ<0时,直线与双曲线没有公共点.
当a=0时,此时直线与双曲线的渐近线平行,直线与双曲线有一个公共点
归纳总结
2.数形结合思想的应用
(1)直线过定点时,根据定点的位置和双曲线的渐近线的斜率与直线的斜率的大小关系确定其位置关系.
(2)直线斜率一定时,通过平行移动直线,比较直线斜率与渐近线斜率的关系来确定其位置关系.
提醒:利用判别式来判断直线与双曲线的交点个数问题的前提是通过消元化为一元二次方程
跟踪训练1 已知双曲线C:x2-y2=1及直线l:y=kx-1,
(1)若直线l与双曲线C有两个不同的交点,求实数k的取值范围;
(2)若直线l与双曲线C交于A,B两点,O是坐标原点,且△AOB的面积为,求实数k的值.
1.已知双曲线-=1(a>0)的离心率为2,则a=( )
A.2 B. C. D.1
2.若一双曲线与椭圆4x2+y2=64有公共的焦点,且它们的离心率互为倒数,则该双曲线的方程为( )
A.y2-3x2=36 B.x2-3y2=36
C.3y2-x2=36 D.3x2-y2=36
3.直线y=mx+1与双曲线x2-y2=1有公共点,则m的取值范围是( )
A.m≥或m≤- B.-≤m≤且m≠0
C.m∈R D.-≤m≤
4.如图为一座高100米的双曲线冷却塔外壳的简化三视图(忽略壁厚),其底面直径大于上底直径,已知其外壳主视图与左视图中的曲线均为双曲线,高度为100,俯视图为三个同心圆,其半径分别40,,30,试根据上述尺寸计算视图中该双曲线的标准方程(为长度单位米);
5.已知双曲线-y2=1,求过点A (3,-1)且被点A平分的弦MN所在直线的方程.
1.双曲线的简单几何性质及其简单应用.
2.直线与双曲线的位置关系.
参考答案:
知识梳理
学习过程
二、典例解析
例4. 解:设双曲线的标准方程为,如图所示:
为喉部直径,故,故双曲线方程为.
而的横坐标为塔顶直径的一半即,
其纵坐标为塔的总高度与喉部标高的差即,
故,
故,所以,
故双曲线方程为.
例5.解:设点,由题知
,,
即.整理得:.
例6、 分析:求弦长问题有两种方法:
法一:如果交点坐标易求,可直接用两点间距离公式代入求弦长;
法二:但有时为了简化计算,常设而不求,运用韦达定理来处理.
解:由双曲线的方程得,两焦点分别为F1(-3,0),F2(3,0).因为直线AB的倾斜角是30°,且直线经过右焦点F2,所以,直线AB的方程为
跟踪训练1[思路探究] 直线方程与双曲线方程联立方程组 判断“Δ”与“0”的关系 直线与双曲线的位置关系.
[解] (1)联立方程组
消去y并整理得(1-k2)x2+2kx-2=0.
∵直线与双曲线有两个不同的交点,
则
解得-<k<,且k≠±1.
∴若l与C有两个不同交点,实数k的取值范围为
(-,-1)∪(-1,1)∪(1,).
(2)设A(x1,y1),B(x2,y2),
对于(1)中的方程(1-k2)x2+2kx-2=0,
由根与系数的关系,得x1+x2=-,
x1x2=-,
∴|AB|=|x1-x2|=
又∵点O(0,0)到直线y=kx-1的距离d=,
∴S△AOB=·|AB|·d==,
即2k4-3k2=0,解得k=0或k=±.
∴实数k的值为±或0.
达标检测
1.【答案】D [由题意得e==2,∴=2a,
∴a2+3=4a2,∴a2=1,∴a=1.]
2.【答案】A [椭圆4x2+y2=64,即+=1,焦点为(0,±4),离心率为,则双曲线的焦点在y轴上,c=4,e=,从而a=6,b2=12,故所求双曲线的方程为y2-3x2=36.]
3.【答案】D [由得(1-m2)x2-2mx-2=0,
由题意知1-m2=0,或
解得-≤m≤.]
4.
【解析】最窄处即双曲线两顶点间
设双曲线的标准方程为:
由题意知:当(地面半径)时对应的值是;
当时,的值为
,解得:
双曲线的标准方程是,
5. [解] 法一 由题意知直线的斜率存在,故可设直线方程为y+1=k(x-3),
即y=kx-3k-1,
由消去y,
整理得(1-4k2)x2+8k(3k+1)x-36k2-24k-8=0.
设M(x1,y1),N(x2,y2),
∴x1+x2=.
∵A(3,-1)为MN的中点,
∴=3,即=3,解得k=-.
当k=-时,满足Δ>0,符合题意,
∴所求直线MN的方程为y=-x+,
即3x+4y-5=0.
法二 设M(x1,y1),N(x2,y2),
∵M,N均在双曲线上,
∴
两式相减,得=y-y,
∴=.
∵点A平分弦MN,∴x1+x2=6,
y1+y2=-2.
∴kMN===-.
经验证,该直线MN存在.
∴所求直线MN的方程为y+1=-(x-3),
即3x+4y-5=0.
1. 掌握双曲线的简单几何性质.
2. 双曲线方程的简单应用.
3. 理解直线与双曲线的位置关系.
重点:直线与双曲线的位置关系
难点:直线与双曲线的位置关系
双曲线的几何性质
标准方程
图形
标准方程
性 质 范围 x≤-a或x≥a y∈R y≤-a或y≥a x∈R
对称性 对称轴:x轴、y轴;对称中心:坐标原点
顶点坐标 A1(-a,0),A2(a,0) A1(0,-a),A2(0,a)
轴 实轴:线段A1A2,长:2a; 虚轴:线段B1B2,长:2b; 半实轴长:a,半虚轴长:b
渐近线 y=± y=±
离心率
a,b,c间的关系 c2=a2+b2(c>a>0,c>b>0)
(1)双曲线与椭圆的六个不同点:
双曲线 椭圆
曲线 两支曲线 封闭的曲线
顶点 两个顶点 四个顶点
轴 实、虚轴 长、短轴
渐近线 有渐近线 无渐近线
离心率 e>1 0
一、典例解析
例4.如图,双曲线型冷却塔的外形,是双曲线的一部分,已知塔的总高度为137.5m,塔顶直径为90m,塔的最小直径(喉部直径)为60m,喉部标高112.5m,试建立适当的坐标系,求出此双曲线的标准方程(精确到1m)
例5.已知点到定点的距离和它到定直线l:的距离的比是,则点的轨迹方程为
请你将例5与椭圆一节中的例6比较,你有什么发现?
例6、 过双曲线的右焦点F2,倾斜角为30度的直线交双曲线于A,B两点,求|AB|.
直线与双曲线位置关系的判断方法
1.方程思想的应用
把直线与双曲线的方程联立成方程组,通过消元后化为ax2+bx+c=0的形式,在a≠0的情况下考察方程的判别式.
(1)Δ>0时,直线与双曲线有两个不同的公共点.
(2)Δ=0时,直线与双曲线只有一个公共点.
(3)Δ<0时,直线与双曲线没有公共点.
当a=0时,此时直线与双曲线的渐近线平行,直线与双曲线有一个公共点
归纳总结
2.数形结合思想的应用
(1)直线过定点时,根据定点的位置和双曲线的渐近线的斜率与直线的斜率的大小关系确定其位置关系.
(2)直线斜率一定时,通过平行移动直线,比较直线斜率与渐近线斜率的关系来确定其位置关系.
提醒:利用判别式来判断直线与双曲线的交点个数问题的前提是通过消元化为一元二次方程
跟踪训练1 已知双曲线C:x2-y2=1及直线l:y=kx-1,
(1)若直线l与双曲线C有两个不同的交点,求实数k的取值范围;
(2)若直线l与双曲线C交于A,B两点,O是坐标原点,且△AOB的面积为,求实数k的值.
1.已知双曲线-=1(a>0)的离心率为2,则a=( )
A.2 B. C. D.1
2.若一双曲线与椭圆4x2+y2=64有公共的焦点,且它们的离心率互为倒数,则该双曲线的方程为( )
A.y2-3x2=36 B.x2-3y2=36
C.3y2-x2=36 D.3x2-y2=36
3.直线y=mx+1与双曲线x2-y2=1有公共点,则m的取值范围是( )
A.m≥或m≤- B.-≤m≤且m≠0
C.m∈R D.-≤m≤
4.如图为一座高100米的双曲线冷却塔外壳的简化三视图(忽略壁厚),其底面直径大于上底直径,已知其外壳主视图与左视图中的曲线均为双曲线,高度为100,俯视图为三个同心圆,其半径分别40,,30,试根据上述尺寸计算视图中该双曲线的标准方程(为长度单位米);
5.已知双曲线-y2=1,求过点A (3,-1)且被点A平分的弦MN所在直线的方程.
1.双曲线的简单几何性质及其简单应用.
2.直线与双曲线的位置关系.
参考答案:
知识梳理
学习过程
二、典例解析
例4. 解:设双曲线的标准方程为,如图所示:
为喉部直径,故,故双曲线方程为.
而的横坐标为塔顶直径的一半即,
其纵坐标为塔的总高度与喉部标高的差即,
故,
故,所以,
故双曲线方程为.
例5.解:设点,由题知
,,
即.整理得:.
例6、 分析:求弦长问题有两种方法:
法一:如果交点坐标易求,可直接用两点间距离公式代入求弦长;
法二:但有时为了简化计算,常设而不求,运用韦达定理来处理.
解:由双曲线的方程得,两焦点分别为F1(-3,0),F2(3,0).因为直线AB的倾斜角是30°,且直线经过右焦点F2,所以,直线AB的方程为
跟踪训练1[思路探究] 直线方程与双曲线方程联立方程组 判断“Δ”与“0”的关系 直线与双曲线的位置关系.
[解] (1)联立方程组
消去y并整理得(1-k2)x2+2kx-2=0.
∵直线与双曲线有两个不同的交点,
则
解得-<k<,且k≠±1.
∴若l与C有两个不同交点,实数k的取值范围为
(-,-1)∪(-1,1)∪(1,).
(2)设A(x1,y1),B(x2,y2),
对于(1)中的方程(1-k2)x2+2kx-2=0,
由根与系数的关系,得x1+x2=-,
x1x2=-,
∴|AB|=|x1-x2|=
又∵点O(0,0)到直线y=kx-1的距离d=,
∴S△AOB=·|AB|·d==,
即2k4-3k2=0,解得k=0或k=±.
∴实数k的值为±或0.
达标检测
1.【答案】D [由题意得e==2,∴=2a,
∴a2+3=4a2,∴a2=1,∴a=1.]
2.【答案】A [椭圆4x2+y2=64,即+=1,焦点为(0,±4),离心率为,则双曲线的焦点在y轴上,c=4,e=,从而a=6,b2=12,故所求双曲线的方程为y2-3x2=36.]
3.【答案】D [由得(1-m2)x2-2mx-2=0,
由题意知1-m2=0,或
解得-≤m≤.]
4.
【解析】最窄处即双曲线两顶点间
设双曲线的标准方程为:
由题意知:当(地面半径)时对应的值是;
当时,的值为
,解得:
双曲线的标准方程是,
5. [解] 法一 由题意知直线的斜率存在,故可设直线方程为y+1=k(x-3),
即y=kx-3k-1,
由消去y,
整理得(1-4k2)x2+8k(3k+1)x-36k2-24k-8=0.
设M(x1,y1),N(x2,y2),
∴x1+x2=.
∵A(3,-1)为MN的中点,
∴=3,即=3,解得k=-.
当k=-时,满足Δ>0,符合题意,
∴所求直线MN的方程为y=-x+,
即3x+4y-5=0.
法二 设M(x1,y1),N(x2,y2),
∵M,N均在双曲线上,
∴
两式相减,得=y-y,
∴=.
∵点A平分弦MN,∴x1+x2=6,
y1+y2=-2.
∴kMN===-.
经验证,该直线MN存在.
∴所求直线MN的方程为y+1=-(x-3),
即3x+4y-5=0.
