3.3.2 抛物线的简单几何性质(1) 导学案
文档属性
| 名称 | 3.3.2 抛物线的简单几何性质(1) 导学案 |
|
|
| 格式 | docx | ||
| 文件大小 | 324.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-29 00:00:00 | ||
图片预览




文档简介
3.3.2 抛物线的简单几何性质(1) 导学案
1.掌握抛物线的简单几何性质.
2.归纳、对比四种方程所表示的抛物线的几何性质的异同.
3.掌握直线与抛物线位置关系的判断。
重点:抛物线的简单几何性质及其应用
难点:直线与抛物线位置关系的判断
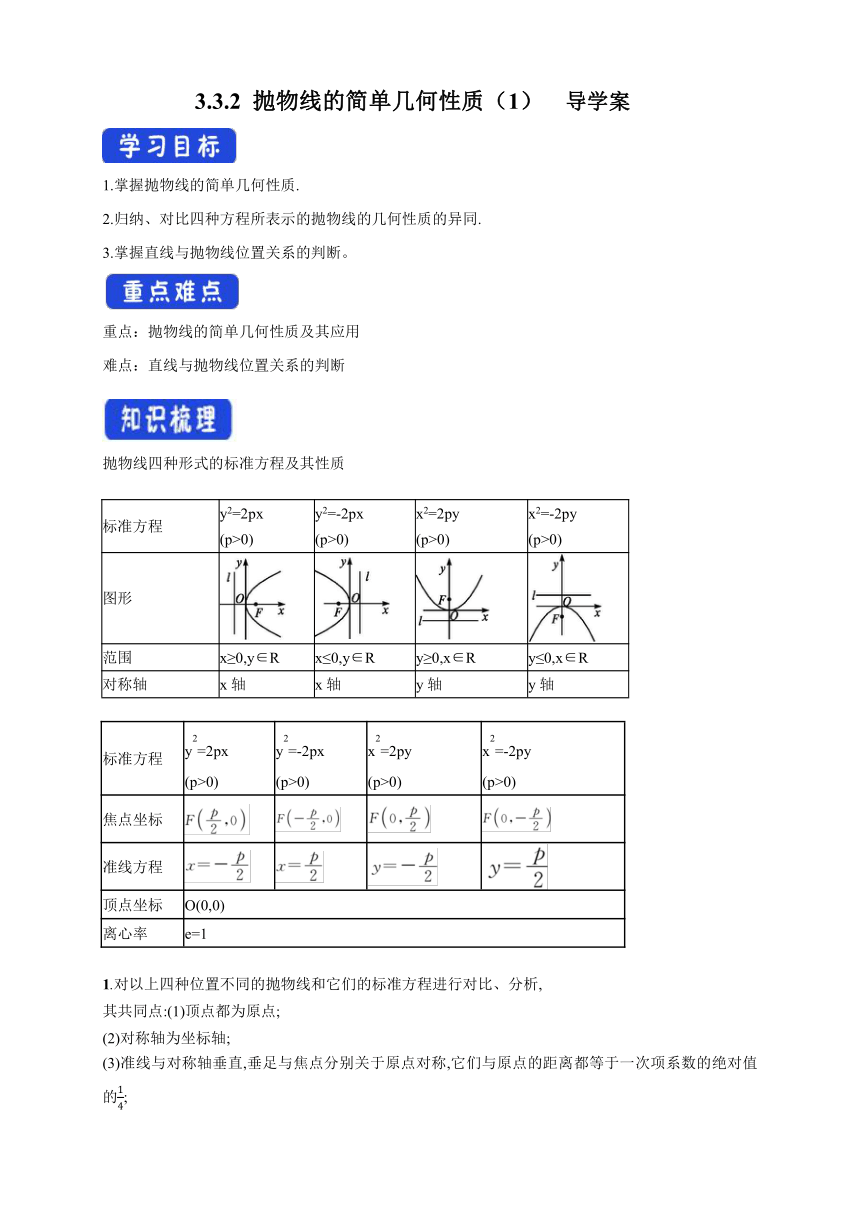
抛物线四种形式的标准方程及其性质
标准方程 y2=2px (p>0) y2=-2px (p>0) x2=2py (p>0) x2=-2py (p>0)
图形
范围 x≥0,y∈R x≤0,y∈R y≥0,x∈R y≤0,x∈R
对称轴 x轴 x轴 y轴 y轴
标准方程 y2=2px (p>0) y2=-2px (p>0) x2=2py (p>0) x2=-2py (p>0)
焦点坐标
准线方程
顶点坐标 O(0,0)
离心率 e=1
1.对以上四种位置不同的抛物线和它们的标准方程进行对比、分析,
其共同点:(1)顶点都为原点;
(2)对称轴为坐标轴;
(3)准线与对称轴垂直,垂足与焦点分别关于原点对称,它们与原点的距离都等于一次项系数的绝对值的;
(4)焦点到准线的距离均为p.
其不同点:(1)对称轴为x轴时,方程的右端为±2px,左端为y2;对称轴为y轴时,方程的右端为±2py,左端为x2;(2)开口方向与x轴(或y轴)的正半轴相同,焦点在x轴(或y轴)的正半轴上,方程的右端取正号;开口方向与x轴(或y轴)的负半轴相同,焦点在x轴(或y轴)的负半轴上,方程的右端取负号.
2.只有焦点在坐标轴上,顶点是原点的抛物线的方程才是标准方程.
1. 判断
(1)抛物线关于顶点对称.( )
(2)抛物线只有一个焦点,一条对称轴,无对称中心.( )
(3)抛物线的标准方程虽然各不相同,但是其离心率都相同.( )
2.思考:怎样根据抛物线的标准方程判断抛物线的对称轴和开口方向
3. 以x轴为对称轴的抛物线的通径(过焦点且与对称轴垂直的弦)长为8,若抛物线的顶点在坐标原点,则其方程为( )
A.y2=8x B.y2=-8x C.y2=8x或y2=-8x D.x2=8y或x2=-8y
问题思考
(1)掌握抛物线的性质,重点应抓住“两点”“两线”“一率”“一方向”,它们分别指的是什么
(2)抛物线的性质与椭圆和双曲线性质的主要区别有哪些
问题导学
类比用方程研究椭圆双曲线几何性质的过程与方法,
①
你认为应研究抛物线的哪些几何性质,如何研究这些性质?
1. 范围
抛物线 y2 = 2px (p>0) 在 y 轴的右侧,开口向右,这条抛物线上的任意一点M 的坐标 (x, y) 的横坐标满足不等式 x ≥ 0;当x 的值增大时,|y| 也增大,这说明抛物线向右上方和右下方无限延伸.抛物线是无界曲线.
2. 对称性
观察图象,不难发现,抛物线 y2 = 2px (p>0)关于 x 轴对称,我们把抛物线的对称轴叫做抛物线的轴.抛物线只有一条对称轴.
3. 顶点
抛物线和它轴的交点叫做抛物线的顶点.抛物线的顶点坐标是坐标原点 (0, 0) .
4. 离心率
抛物线上的点M 到焦点的距离和它到准线的距离的比,叫做抛物线的离心率. 用 e 表示,e = 1.
探究
如果抛物线的标准方程是
②
③
④
那么抛物线的范围(开口方向)、对称性、顶点、离心率中,哪些与①所表示的抛物线是相同的?哪些是有区别的?
二、典例解析
例3. 已知轴,顶点是坐标原点,并且经过点M
求它的标准方程。
顶点在原点,对称轴是坐标轴,并且经过点M 的抛物线有几条?求出这些抛物线的标准方程。
跟踪训练1 .设抛物线y=mx2(m≠0)的准线与直线y=1的距离为3,求抛物线的标准方程.
例4 .斜率为 1 的直线经过抛物线 y2 = 4x 的焦点,与抛物线相交于两点A、B,求焦点弦长AB的长.
直线和抛物线的位置关系有三种:相交、相切、相离
将直线方程和抛物线方程联立,消元转化为关于 x(或 y 的)
方程组:Ax2 + Bx + C = 0(或Ay2 + By + C = 0),其中A,B,C 为常数.
若A = 0,则直线和抛物线相交(直线与抛物线的对称轴平行),有一个交点;
若A ≠ 0,计算判别式 Δ=B2 -4AC :
若 Δ>0,则直线和抛物线相交(有两个交点);
若 Δ = 0,则直线和抛物线相切(有一个交点);
若 Δ<0,则直线和抛物线相离(无交点).
跟踪训练2 (1)过定点P(0,1)作与抛物线y2=2x只有一个公共点的直线有几条?
(2)若直线l:y=(a+1)x-1与曲线C:y2=ax(a≠0)恰好有一个公共点,试求实数a的取值集合.
1.若抛物线y2=2x上有两点A、B且AB垂直于x轴,若|AB|=2,则抛物线的焦点到直线AB的距离为( )
A. B. C. D.
2.在抛物线y2=16x上到顶点与到焦点距离相等的点的坐标为( )
A.(4,±2) B.(±4,2) C.(±2,4) D.(2,±4)
3.已知AB是过抛物线2x2=y的焦点的弦,若|AB|=4,则AB的中点的纵坐标是________.
4. 已知抛物线y2=8x.
(1)求出该抛物线的顶点、焦点、准线方程、对称轴、变量x的范围;
(2)以坐标原点O为顶点,作抛物线的内接等腰三角形OAB,|OA|=|OB|,若焦点F是△OAB的重心,求△OAB的周长.
5.已知点P(1,m)是抛物线C:y2=2px上的点,F为抛物线的焦点,且|PF|=2,直线l:y=k(x-1)与抛物线C相交于不同的两点A,B.
(1)求抛物线C的方程;
(2)若|AB|=8,求k的值.
参考答案:
知识梳理
1. 判断答案:(1)× (2)√ (3)√
2.解析:一次项的变量若为x(或y),则x轴(或y轴)是抛物线的对称轴,一次项系数的
符号决定开口方向.
如果y是一次项,负时向下,正时向上.
如果x是一次项,负时向左,正时向右.
3. 解析:设抛物线方程为y2=2px(p>0)或y2=-2px(p>0),依题意得x=,代入y2=2px或y2=-2px
得|y|=p,∴2|y|=2p=8,p=4.∴抛物线方程为y2=8x或y2=-8x.
答案:C
问题思考
(1)提示:“两点”是指抛物线的焦点和顶点;“两线”是指抛物线的准线和对称轴;“一率”是指离心率1;“一方向”是指抛物线的开口方向.
(2)提示:抛物线的离心率等于1,它只有一个焦点、一个顶点、一条对称轴和一条准线.它没有中心,通常称抛物线为无心圆锥曲线,而称椭圆和双曲线为有心圆锥曲线.
学习过程
一、问题导学
二、典例解析
例3. 解:因为轴,它的顶点在原点,并且经过点M ,所以可设它的标准方程为
因为点M
解得= 因此,所求抛物线的标准方程是
跟踪训练1 .错解:由y=mx2(m≠0)可知其准线方程为y=-.
由题意知-=-2,解得m=8,
故所求抛物线的标准方程为y=8x2.
错因分析本题在解答过程中容易出现两个错误:一是不能正确理解抛物线标准方程的形式,错误地将所给方程看成是抛物线的标准方程,得到准线方程为y=- ;
二是得到准线方程后,只分析其中的一种情况,而忽略了另一种情况,只得到了一个解.
正解:y=mx2(m≠0)可化为x2=y,其准线方程为y=-.由题意知-=-2或-=4,
解得m=或m=-,
故所求抛物线的标准方程为x2=8y或x2=-16y.
例4 . 解:方法一:由抛物线的标准方程可知,抛物线焦点的坐标为F (1,0),
所以直线AB的方程为,即, ①
将方程①代入抛物线方程,化简得,
解这个方程,得,,
将,代入方程①中,
得,,即A(,),B(,),
∴.
解:方法二:由抛物线的定义可知,|AF|=|AD|=x1+1,|BF|=|BC|= x2+1,
于是|AB|=|AF|+|BF|= x1+x2+2.
在方法一中得到方程x2-6x+1=0后,
根据根与系数的关系可以直接得到x1+x2=6,
于是立即可以求出|AB|=6+2=8.
方法三:抛物线y2=4x中2p=4,直线的
倾斜角为,所以焦点弦长.
跟踪训练2 [思路探究] (1)分斜率存在、不存在两种情况,存在时将直线方程代入抛物线方程,转化为Δ=0求解;不存在时显然满足题意.
(2)→
→分类讨论方程有一解时a的取值
[解] (1)当直线的斜率不存在时,直线x=0,符合题意.
当直线的斜率存在时,设过点P的直线方程为y=kx+1,当k=0时,直线l的方程为y=1,满足直线与抛物线y2=2x仅有一个公共点;
当k≠0时,将直线方程y=kx+1代入y2=2x,消去y得k2x2+2(k-1)x+1=0.由Δ=0,得k=,直线方程为y=x+1.故满足条件的直线有三条.
(2)因为直线l与曲线C恰好有一个公共点,所以方程组只有一组实数解,消去y,得[(a+1)x-1]2=ax,即(a+1)2x2-(3a+2)x+1=0 ①.
(ⅰ)当a+1=0,即a=-1时,方程①是关于x的一元一次方程,解得x=-1,这时,原方程组有唯一解
(ⅱ)当a+1≠0,即a≠-1时,方程①是关于x的一元二次方程.
令Δ=(3a+2)2-4(a+1)2=a(5a+4)=0,解得a=0(舍去)或a=-.
所以原方程组有唯一解
综上,实数a的取值集合是.
达标检测
1.A [线段AB所在的直线方程为x=1,抛物线的焦点坐标为,则焦点到直线AB的距离为1-=.]
2.D [抛物线y2=16x的顶点O(0,0),焦点F(4,0),设P(x,y)符合题意,则有
所以符合题意的点为(2,±4).]
3. [设A(x1,y1),B(x2,y2),由抛物线2x2=y,可得p=.
∵|AB|=y1+y2+p=4,∴y1+y2=4-=,故AB的中点的纵坐标是=.]
4. 解:(1)抛物线y2=8x的顶点、焦点、准线方程、对称轴、变量x的范围分别为(0,0),(2,0),x=-2,x轴,x≥0.
(2)如图所示,由|OA|=|OB|可知AB⊥x轴,垂足为点M,
又焦点F是△OAB的重心,
则|OF|=|OM|. 因为F(2,0),
所以|OM|=|OF|=3,所以M(3,0).故设A(3,m),
代入y2=8x得m2=24, 所以m=2或m=-2,
所以A(3,2),B(3,-2),所以|OA|=|OB|=,
所以△OAB的周长为2+4.
5.[解] (1)抛物线C:y2=2px的准线为x=-,
由|PF|=2得:1+=2,得p=2.
所以抛物线的方程为y2=4x.
(2)设A(x1,y1),B(x2,y2),由
可得k2x2-(2k2+4)x+k2=0,Δ=16k2+16>0,
∴x1+x2=.
∵直线l经过抛物线C的焦点F,
∴|AB|=x1+x2+p=+2=8,
解得k=±1,所以k的值为1或-1.
1.掌握抛物线的简单几何性质.
2.归纳、对比四种方程所表示的抛物线的几何性质的异同.
3.掌握直线与抛物线位置关系的判断。
重点:抛物线的简单几何性质及其应用
难点:直线与抛物线位置关系的判断
抛物线四种形式的标准方程及其性质
标准方程 y2=2px (p>0) y2=-2px (p>0) x2=2py (p>0) x2=-2py (p>0)
图形
范围 x≥0,y∈R x≤0,y∈R y≥0,x∈R y≤0,x∈R
对称轴 x轴 x轴 y轴 y轴
标准方程 y2=2px (p>0) y2=-2px (p>0) x2=2py (p>0) x2=-2py (p>0)
焦点坐标
准线方程
顶点坐标 O(0,0)
离心率 e=1
1.对以上四种位置不同的抛物线和它们的标准方程进行对比、分析,
其共同点:(1)顶点都为原点;
(2)对称轴为坐标轴;
(3)准线与对称轴垂直,垂足与焦点分别关于原点对称,它们与原点的距离都等于一次项系数的绝对值的;
(4)焦点到准线的距离均为p.
其不同点:(1)对称轴为x轴时,方程的右端为±2px,左端为y2;对称轴为y轴时,方程的右端为±2py,左端为x2;(2)开口方向与x轴(或y轴)的正半轴相同,焦点在x轴(或y轴)的正半轴上,方程的右端取正号;开口方向与x轴(或y轴)的负半轴相同,焦点在x轴(或y轴)的负半轴上,方程的右端取负号.
2.只有焦点在坐标轴上,顶点是原点的抛物线的方程才是标准方程.
1. 判断
(1)抛物线关于顶点对称.( )
(2)抛物线只有一个焦点,一条对称轴,无对称中心.( )
(3)抛物线的标准方程虽然各不相同,但是其离心率都相同.( )
2.思考:怎样根据抛物线的标准方程判断抛物线的对称轴和开口方向
3. 以x轴为对称轴的抛物线的通径(过焦点且与对称轴垂直的弦)长为8,若抛物线的顶点在坐标原点,则其方程为( )
A.y2=8x B.y2=-8x C.y2=8x或y2=-8x D.x2=8y或x2=-8y
问题思考
(1)掌握抛物线的性质,重点应抓住“两点”“两线”“一率”“一方向”,它们分别指的是什么
(2)抛物线的性质与椭圆和双曲线性质的主要区别有哪些
问题导学
类比用方程研究椭圆双曲线几何性质的过程与方法,
①
你认为应研究抛物线的哪些几何性质,如何研究这些性质?
1. 范围
抛物线 y2 = 2px (p>0) 在 y 轴的右侧,开口向右,这条抛物线上的任意一点M 的坐标 (x, y) 的横坐标满足不等式 x ≥ 0;当x 的值增大时,|y| 也增大,这说明抛物线向右上方和右下方无限延伸.抛物线是无界曲线.
2. 对称性
观察图象,不难发现,抛物线 y2 = 2px (p>0)关于 x 轴对称,我们把抛物线的对称轴叫做抛物线的轴.抛物线只有一条对称轴.
3. 顶点
抛物线和它轴的交点叫做抛物线的顶点.抛物线的顶点坐标是坐标原点 (0, 0) .
4. 离心率
抛物线上的点M 到焦点的距离和它到准线的距离的比,叫做抛物线的离心率. 用 e 表示,e = 1.
探究
如果抛物线的标准方程是
②
③
④
那么抛物线的范围(开口方向)、对称性、顶点、离心率中,哪些与①所表示的抛物线是相同的?哪些是有区别的?
二、典例解析
例3. 已知轴,顶点是坐标原点,并且经过点M
求它的标准方程。
顶点在原点,对称轴是坐标轴,并且经过点M 的抛物线有几条?求出这些抛物线的标准方程。
跟踪训练1 .设抛物线y=mx2(m≠0)的准线与直线y=1的距离为3,求抛物线的标准方程.
例4 .斜率为 1 的直线经过抛物线 y2 = 4x 的焦点,与抛物线相交于两点A、B,求焦点弦长AB的长.
直线和抛物线的位置关系有三种:相交、相切、相离
将直线方程和抛物线方程联立,消元转化为关于 x(或 y 的)
方程组:Ax2 + Bx + C = 0(或Ay2 + By + C = 0),其中A,B,C 为常数.
若A = 0,则直线和抛物线相交(直线与抛物线的对称轴平行),有一个交点;
若A ≠ 0,计算判别式 Δ=B2 -4AC :
若 Δ>0,则直线和抛物线相交(有两个交点);
若 Δ = 0,则直线和抛物线相切(有一个交点);
若 Δ<0,则直线和抛物线相离(无交点).
跟踪训练2 (1)过定点P(0,1)作与抛物线y2=2x只有一个公共点的直线有几条?
(2)若直线l:y=(a+1)x-1与曲线C:y2=ax(a≠0)恰好有一个公共点,试求实数a的取值集合.
1.若抛物线y2=2x上有两点A、B且AB垂直于x轴,若|AB|=2,则抛物线的焦点到直线AB的距离为( )
A. B. C. D.
2.在抛物线y2=16x上到顶点与到焦点距离相等的点的坐标为( )
A.(4,±2) B.(±4,2) C.(±2,4) D.(2,±4)
3.已知AB是过抛物线2x2=y的焦点的弦,若|AB|=4,则AB的中点的纵坐标是________.
4. 已知抛物线y2=8x.
(1)求出该抛物线的顶点、焦点、准线方程、对称轴、变量x的范围;
(2)以坐标原点O为顶点,作抛物线的内接等腰三角形OAB,|OA|=|OB|,若焦点F是△OAB的重心,求△OAB的周长.
5.已知点P(1,m)是抛物线C:y2=2px上的点,F为抛物线的焦点,且|PF|=2,直线l:y=k(x-1)与抛物线C相交于不同的两点A,B.
(1)求抛物线C的方程;
(2)若|AB|=8,求k的值.
参考答案:
知识梳理
1. 判断答案:(1)× (2)√ (3)√
2.解析:一次项的变量若为x(或y),则x轴(或y轴)是抛物线的对称轴,一次项系数的
符号决定开口方向.
如果y是一次项,负时向下,正时向上.
如果x是一次项,负时向左,正时向右.
3. 解析:设抛物线方程为y2=2px(p>0)或y2=-2px(p>0),依题意得x=,代入y2=2px或y2=-2px
得|y|=p,∴2|y|=2p=8,p=4.∴抛物线方程为y2=8x或y2=-8x.
答案:C
问题思考
(1)提示:“两点”是指抛物线的焦点和顶点;“两线”是指抛物线的准线和对称轴;“一率”是指离心率1;“一方向”是指抛物线的开口方向.
(2)提示:抛物线的离心率等于1,它只有一个焦点、一个顶点、一条对称轴和一条准线.它没有中心,通常称抛物线为无心圆锥曲线,而称椭圆和双曲线为有心圆锥曲线.
学习过程
一、问题导学
二、典例解析
例3. 解:因为轴,它的顶点在原点,并且经过点M ,所以可设它的标准方程为
因为点M
解得= 因此,所求抛物线的标准方程是
跟踪训练1 .错解:由y=mx2(m≠0)可知其准线方程为y=-.
由题意知-=-2,解得m=8,
故所求抛物线的标准方程为y=8x2.
错因分析本题在解答过程中容易出现两个错误:一是不能正确理解抛物线标准方程的形式,错误地将所给方程看成是抛物线的标准方程,得到准线方程为y=- ;
二是得到准线方程后,只分析其中的一种情况,而忽略了另一种情况,只得到了一个解.
正解:y=mx2(m≠0)可化为x2=y,其准线方程为y=-.由题意知-=-2或-=4,
解得m=或m=-,
故所求抛物线的标准方程为x2=8y或x2=-16y.
例4 . 解:方法一:由抛物线的标准方程可知,抛物线焦点的坐标为F (1,0),
所以直线AB的方程为,即, ①
将方程①代入抛物线方程,化简得,
解这个方程,得,,
将,代入方程①中,
得,,即A(,),B(,),
∴.
解:方法二:由抛物线的定义可知,|AF|=|AD|=x1+1,|BF|=|BC|= x2+1,
于是|AB|=|AF|+|BF|= x1+x2+2.
在方法一中得到方程x2-6x+1=0后,
根据根与系数的关系可以直接得到x1+x2=6,
于是立即可以求出|AB|=6+2=8.
方法三:抛物线y2=4x中2p=4,直线的
倾斜角为,所以焦点弦长.
跟踪训练2 [思路探究] (1)分斜率存在、不存在两种情况,存在时将直线方程代入抛物线方程,转化为Δ=0求解;不存在时显然满足题意.
(2)→
→分类讨论方程有一解时a的取值
[解] (1)当直线的斜率不存在时,直线x=0,符合题意.
当直线的斜率存在时,设过点P的直线方程为y=kx+1,当k=0时,直线l的方程为y=1,满足直线与抛物线y2=2x仅有一个公共点;
当k≠0时,将直线方程y=kx+1代入y2=2x,消去y得k2x2+2(k-1)x+1=0.由Δ=0,得k=,直线方程为y=x+1.故满足条件的直线有三条.
(2)因为直线l与曲线C恰好有一个公共点,所以方程组只有一组实数解,消去y,得[(a+1)x-1]2=ax,即(a+1)2x2-(3a+2)x+1=0 ①.
(ⅰ)当a+1=0,即a=-1时,方程①是关于x的一元一次方程,解得x=-1,这时,原方程组有唯一解
(ⅱ)当a+1≠0,即a≠-1时,方程①是关于x的一元二次方程.
令Δ=(3a+2)2-4(a+1)2=a(5a+4)=0,解得a=0(舍去)或a=-.
所以原方程组有唯一解
综上,实数a的取值集合是.
达标检测
1.A [线段AB所在的直线方程为x=1,抛物线的焦点坐标为,则焦点到直线AB的距离为1-=.]
2.D [抛物线y2=16x的顶点O(0,0),焦点F(4,0),设P(x,y)符合题意,则有
所以符合题意的点为(2,±4).]
3. [设A(x1,y1),B(x2,y2),由抛物线2x2=y,可得p=.
∵|AB|=y1+y2+p=4,∴y1+y2=4-=,故AB的中点的纵坐标是=.]
4. 解:(1)抛物线y2=8x的顶点、焦点、准线方程、对称轴、变量x的范围分别为(0,0),(2,0),x=-2,x轴,x≥0.
(2)如图所示,由|OA|=|OB|可知AB⊥x轴,垂足为点M,
又焦点F是△OAB的重心,
则|OF|=|OM|. 因为F(2,0),
所以|OM|=|OF|=3,所以M(3,0).故设A(3,m),
代入y2=8x得m2=24, 所以m=2或m=-2,
所以A(3,2),B(3,-2),所以|OA|=|OB|=,
所以△OAB的周长为2+4.
5.[解] (1)抛物线C:y2=2px的准线为x=-,
由|PF|=2得:1+=2,得p=2.
所以抛物线的方程为y2=4x.
(2)设A(x1,y1),B(x2,y2),由
可得k2x2-(2k2+4)x+k2=0,Δ=16k2+16>0,
∴x1+x2=.
∵直线l经过抛物线C的焦点F,
∴|AB|=x1+x2+p=+2=8,
解得k=±1,所以k的值为1或-1.
