5.1.2导数的概念及其几何意义 (导学案)
文档属性
| 名称 | 5.1.2导数的概念及其几何意义 (导学案) |  | |
| 格式 | docx | ||
| 文件大小 | 316.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-29 23:00:09 | ||
图片预览


文档简介
5.1.2导数的概念及其几何意义 导学案
1. 经历由平均变化率到瞬时变化率的过程,体会导数的概念的实际背景.
2.了解导函数的概念,理解导数的几何意义.
重点:导数的概念及其几何意义
难点:导数中蕴含的极限思想和以直代曲的思想方法的理解
1.导数的概念
如果当Δx→0时,平均变化率无限趋近于一个确定的值,即有极限,则称y=f (x)在x=x0处____,并把这个________叫做y=f (x)在x=x0处的导数(也称为__________),记作f ′(x0)或________,即
f ′(x0)= = .
可导; 确定的值; 瞬时变化率; y′|; ;
2.导数的几何意义
(1)导数的几何意义
如图,割线P0P的斜率k=___________.记Δx=x-x0,当点P沿着曲线y=f (x)无限趋近于点P0时,即当Δx→0时,k无限趋近于函数y=f (x)在x=x0处的导数,因此,函数y=f (x)在x=x0处的导数f ′(x0)就是__________的斜率k0,即k0= =f ′(x0).
;切线P0T
3.导函数
对于函数y=f (x),当x=x0时,f ′(x0)是一个唯一确定的数,当x变化时,f ′(x)便是x的一个函数,我们称它为y=f (x)的导函数(简称为导数),即f ′(x)=y′= .
学习导引
前面我们研究了两类变化率问题:一类是物理学中的问题,涉及平均速度和瞬时速度;另一类是几何学中的问题,涉及割线斜率和切线斜率。这两类问题来自不同的学科领域,但在解决问题时,都采用了由“平均变化率”逼近“瞬时变化率”的思想方法;问题的答案也是一样的表示形式。下面我们用上述思想方法研究更一般的问题。
二、新知探究
探究1:对于函数,设自变量从变化到+ ,相应地,函数值就从变化到。这时, 的变化量为
的变化量为
我们把比值,即=
叫做函数从到的平均变化率。
由导数的定义可知,问题1中运动员在t =1时的瞬时速度,就是函数h(t)=-4.9t2+4.8t+11.
在t =1处的导数(1) ;问题2中抛物线在点(1,1)
处的切线T的斜率,就是函数在x =1处的导数(1) ,实际上,导数可以描述任何运动变化事物的瞬时变化率,如效率、国内生产总值(GDP)的增长率等。
探究2: 我们知道,导数表示函数在处的瞬时变化率,反映了函数在附近的变化情况,那么导数的几何意义是什么?
观察函数,
平均变化率
=表示什么
瞬时变化率
==表示什么?
三、典例解析
例1 设 求.
利用导数定义求导数
取极限前,要注意化简,保证使Δx→0时分母不为0.
函数在x0处的导数f ′x0只与x0有关,与Δx无关.
导数可以描述事物的瞬时变化率,应用非常广泛.
跟踪训练1. (1)若函数y=f (x)在x=x0处可导,则 等于( )
A.f ′(x0) B.2f ′(x0) C.-2f ′(x0) D.0
(2)求函数y=3x2在x=1处的导数.
跟踪训练2.建造一栋面积为x m2的房屋需要成本y万元,y是x的函数,y=f (x)=++0.3,求f ′(100),并解释它的实际意义.
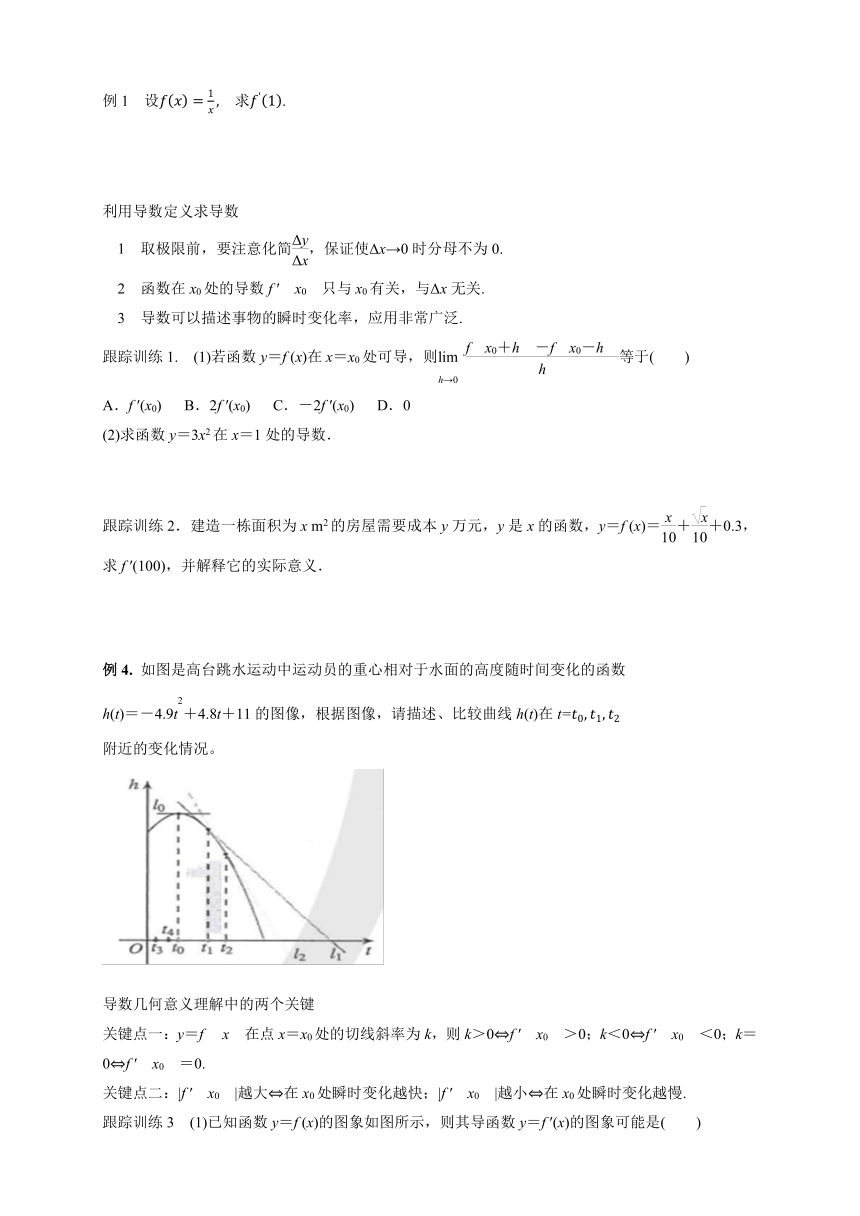
例4. 如图是高台跳水运动中运动员的重心相对于水面的高度随时间变化的函数
h(t)=-4.9t2+4.8t+11的图像,根据图像,请描述、比较曲线h(t)在t=
附近的变化情况。
导数几何意义理解中的两个关键
关键点一:y=f x在点x=x0处的切线斜率为k,则k>0 f ′x0>0;k<0 f ′x0<0;k=0 f ′x0=0.
关键点二:|f ′x0越大 在x0处瞬时变化越快;|f ′x0越小 在x0处瞬时变化越慢.
跟踪训练3 (1)已知函数y=f (x)的图象如图所示,则其导函数y=f ′(x)的图象可能是( )
A B C D
(2)某家电制造集团为尽快实现家电下乡提出四种运输方案,据预测,这四种方案均能在规定时间T内完成预期的运输任务Q0,各种方案的运输总量Q与时间t的函数关系如下所示.在这四种方案中,运输效率(单位时间内的运输量)逐步提高的是( )
A B C D
1.判断正误(正确的打“√”,错误的打“×”)
(1)函数y=f (x)在x=x0处的导数即为在该点处的斜率,也就是k=f ′(x0). ( )
(2)f ′(x1)>f ′(x2)反映了曲线在x=x1处比在x=x2处瞬时变化率较大. ( )
(3)f ′(x0)就是导函数y=f ′(x)在x0处的函数值. ( )
(4)若f ′(x0)=0,则曲线在x=x0处切线不存在. ( )
2.已知函数y=f (x)是可导函数,且f ′(1)=2,则 =( )
A. B.2 C.1 D.-1
3.已知y=f (x)的图象如图所示,则f ′(xA)与f ′(xB)的大小关系是( )
A.f ′(xA)>f ′(xB) B.f ′(xA)<f ′(xB)
C.f ′(xA)=f ′(xB) D.不能确定
4.若曲线y=x2+ax+b在点(0,b)处的切线方程是x-y+1=0,则( )
A.a=1,b=1 B.a=-1,b=1
C.a=1,b=-1 D.a=-1,b=-1
5.已知曲线y=2x2-7在点P处的切线方程为8x-y-15=0,求切点P的坐标.
1.导函数的概念;
2.导数的几何意义;
3.导函数的概念.
参考答案:
知识梳理
学习过程
新知探究
典例解析
例1 解:=
=1
跟踪训练1. (1)B [∵Δx=(x0+h)-(x0-h)=2h.
∴ =2 =2f ′(x0).故选B.]
(2)解:∵Δy=f (1+Δx)-f (1)=3(1+Δx)2-3=6Δx+3(Δx)2,
∴=6+3Δx,
∴f ′(1)= = (6+3Δx)=6.
跟踪训练2. [解] 根据导数的定义,得
f ′(100)=
=
=
=
=
=+
=0.105.
f ′(100)=0.105表示当建筑面积为100 m2时,成本增加的速度为1 050元/m2.
例4. 解:我们用曲线h(t)在t=处的切线斜率,刻画曲线h(t) 在上述三个时刻附近的变化情况
(1)当t=时,曲线h(t)在t=处的切线平行于t轴,=0,
这时,在t=附近曲线比较平坦,几乎没有升降;
(2)当t=时,曲线h(t)在t=处的切线斜率<0,这时,
在t=附近曲线下降,即函数h(t)在t=附近单调递减;
(3)当t=时,曲线h(t)在t=处的切线斜率<0,
这时,在t=附近曲线下降,即函数h(t)在t=附近单调递减;
从图可以看出,直线倾斜程度小于直线倾斜程度,这说明曲线h(t)在t=附近比在t=附近下降得缓慢。
跟踪训练3 [思路探究] (1)切线斜率大于零,则f ′(x)>0;切线斜率小于零,则f ′(x)<0;
(2)要明确运输效率的含义,题设中已经给出运输效率即单位时间内的运输量,因此,运输效率逐步提高就是指Q′(t)不断增大.
(1)B (2)B [(1)由y=f (x)的图象及导数的几何意义可知,当x<0时,f ′(x)>0;当x=0时,f ′(x)=0;当x>0时,f ′(x)<0,故B符合.
(2)从函数图象上看,要求图象在[0,T]上越来越陡峭,在各选项中,只有B项中图象的切线斜率在不断增大,即运输效率(单位时间内的运输量)逐步提高.故选B.]
达标检测
1.解析: (1)根据导数的几何意义知正确.
(2)若|f (x0)|越大,瞬时变化率越大,故错误.
(3)根据导函数的定义知正确.
(4)若f ′(x0)=0说明曲线在x=x0处切线平行于x轴,不能说不存在.
[答案] (1)√ (2)× (3)√ (4)×
2.C [由题意可得: = =f ′(1),
即: =×2=1.故应选C.]
3. B 解析:由导数的几何意义,f ′(xA),f ′(xB)分别是切线在点A、B处切线的斜率,
由图象可知f ′(xA)<f ′(xB).
4.A 解析:由题意,知k=y′|x=0= =1,
∴a=1.又点(0,b)在切线上,∴b=1,故选A.
5. [解] 设切点P(m,n),切线斜率为k,
由y′= = = (4x+2Δx)=4x,
得k=y′|x=m=4m.
由题意可知4m=8,∴m=2.
代入y=2x2-7得n=1.
故所求切点P为(2,1).
1. 经历由平均变化率到瞬时变化率的过程,体会导数的概念的实际背景.
2.了解导函数的概念,理解导数的几何意义.
重点:导数的概念及其几何意义
难点:导数中蕴含的极限思想和以直代曲的思想方法的理解
1.导数的概念
如果当Δx→0时,平均变化率无限趋近于一个确定的值,即有极限,则称y=f (x)在x=x0处____,并把这个________叫做y=f (x)在x=x0处的导数(也称为__________),记作f ′(x0)或________,即
f ′(x0)= = .
可导; 确定的值; 瞬时变化率; y′|; ;
2.导数的几何意义
(1)导数的几何意义
如图,割线P0P的斜率k=___________.记Δx=x-x0,当点P沿着曲线y=f (x)无限趋近于点P0时,即当Δx→0时,k无限趋近于函数y=f (x)在x=x0处的导数,因此,函数y=f (x)在x=x0处的导数f ′(x0)就是__________的斜率k0,即k0= =f ′(x0).
;切线P0T
3.导函数
对于函数y=f (x),当x=x0时,f ′(x0)是一个唯一确定的数,当x变化时,f ′(x)便是x的一个函数,我们称它为y=f (x)的导函数(简称为导数),即f ′(x)=y′= .
学习导引
前面我们研究了两类变化率问题:一类是物理学中的问题,涉及平均速度和瞬时速度;另一类是几何学中的问题,涉及割线斜率和切线斜率。这两类问题来自不同的学科领域,但在解决问题时,都采用了由“平均变化率”逼近“瞬时变化率”的思想方法;问题的答案也是一样的表示形式。下面我们用上述思想方法研究更一般的问题。
二、新知探究
探究1:对于函数,设自变量从变化到+ ,相应地,函数值就从变化到。这时, 的变化量为
的变化量为
我们把比值,即=
叫做函数从到的平均变化率。
由导数的定义可知,问题1中运动员在t =1时的瞬时速度,就是函数h(t)=-4.9t2+4.8t+11.
在t =1处的导数(1) ;问题2中抛物线在点(1,1)
处的切线T的斜率,就是函数在x =1处的导数(1) ,实际上,导数可以描述任何运动变化事物的瞬时变化率,如效率、国内生产总值(GDP)的增长率等。
探究2: 我们知道,导数表示函数在处的瞬时变化率,反映了函数在附近的变化情况,那么导数的几何意义是什么?
观察函数,
平均变化率
=表示什么
瞬时变化率
==表示什么?
三、典例解析
例1 设 求.
利用导数定义求导数
取极限前,要注意化简,保证使Δx→0时分母不为0.
函数在x0处的导数f ′x0只与x0有关,与Δx无关.
导数可以描述事物的瞬时变化率,应用非常广泛.
跟踪训练1. (1)若函数y=f (x)在x=x0处可导,则 等于( )
A.f ′(x0) B.2f ′(x0) C.-2f ′(x0) D.0
(2)求函数y=3x2在x=1处的导数.
跟踪训练2.建造一栋面积为x m2的房屋需要成本y万元,y是x的函数,y=f (x)=++0.3,求f ′(100),并解释它的实际意义.
例4. 如图是高台跳水运动中运动员的重心相对于水面的高度随时间变化的函数
h(t)=-4.9t2+4.8t+11的图像,根据图像,请描述、比较曲线h(t)在t=
附近的变化情况。
导数几何意义理解中的两个关键
关键点一:y=f x在点x=x0处的切线斜率为k,则k>0 f ′x0>0;k<0 f ′x0<0;k=0 f ′x0=0.
关键点二:|f ′x0越大 在x0处瞬时变化越快;|f ′x0越小 在x0处瞬时变化越慢.
跟踪训练3 (1)已知函数y=f (x)的图象如图所示,则其导函数y=f ′(x)的图象可能是( )
A B C D
(2)某家电制造集团为尽快实现家电下乡提出四种运输方案,据预测,这四种方案均能在规定时间T内完成预期的运输任务Q0,各种方案的运输总量Q与时间t的函数关系如下所示.在这四种方案中,运输效率(单位时间内的运输量)逐步提高的是( )
A B C D
1.判断正误(正确的打“√”,错误的打“×”)
(1)函数y=f (x)在x=x0处的导数即为在该点处的斜率,也就是k=f ′(x0). ( )
(2)f ′(x1)>f ′(x2)反映了曲线在x=x1处比在x=x2处瞬时变化率较大. ( )
(3)f ′(x0)就是导函数y=f ′(x)在x0处的函数值. ( )
(4)若f ′(x0)=0,则曲线在x=x0处切线不存在. ( )
2.已知函数y=f (x)是可导函数,且f ′(1)=2,则 =( )
A. B.2 C.1 D.-1
3.已知y=f (x)的图象如图所示,则f ′(xA)与f ′(xB)的大小关系是( )
A.f ′(xA)>f ′(xB) B.f ′(xA)<f ′(xB)
C.f ′(xA)=f ′(xB) D.不能确定
4.若曲线y=x2+ax+b在点(0,b)处的切线方程是x-y+1=0,则( )
A.a=1,b=1 B.a=-1,b=1
C.a=1,b=-1 D.a=-1,b=-1
5.已知曲线y=2x2-7在点P处的切线方程为8x-y-15=0,求切点P的坐标.
1.导函数的概念;
2.导数的几何意义;
3.导函数的概念.
参考答案:
知识梳理
学习过程
新知探究
典例解析
例1 解:=
=1
跟踪训练1. (1)B [∵Δx=(x0+h)-(x0-h)=2h.
∴ =2 =2f ′(x0).故选B.]
(2)解:∵Δy=f (1+Δx)-f (1)=3(1+Δx)2-3=6Δx+3(Δx)2,
∴=6+3Δx,
∴f ′(1)= = (6+3Δx)=6.
跟踪训练2. [解] 根据导数的定义,得
f ′(100)=
=
=
=
=
=+
=0.105.
f ′(100)=0.105表示当建筑面积为100 m2时,成本增加的速度为1 050元/m2.
例4. 解:我们用曲线h(t)在t=处的切线斜率,刻画曲线h(t) 在上述三个时刻附近的变化情况
(1)当t=时,曲线h(t)在t=处的切线平行于t轴,=0,
这时,在t=附近曲线比较平坦,几乎没有升降;
(2)当t=时,曲线h(t)在t=处的切线斜率<0,这时,
在t=附近曲线下降,即函数h(t)在t=附近单调递减;
(3)当t=时,曲线h(t)在t=处的切线斜率<0,
这时,在t=附近曲线下降,即函数h(t)在t=附近单调递减;
从图可以看出,直线倾斜程度小于直线倾斜程度,这说明曲线h(t)在t=附近比在t=附近下降得缓慢。
跟踪训练3 [思路探究] (1)切线斜率大于零,则f ′(x)>0;切线斜率小于零,则f ′(x)<0;
(2)要明确运输效率的含义,题设中已经给出运输效率即单位时间内的运输量,因此,运输效率逐步提高就是指Q′(t)不断增大.
(1)B (2)B [(1)由y=f (x)的图象及导数的几何意义可知,当x<0时,f ′(x)>0;当x=0时,f ′(x)=0;当x>0时,f ′(x)<0,故B符合.
(2)从函数图象上看,要求图象在[0,T]上越来越陡峭,在各选项中,只有B项中图象的切线斜率在不断增大,即运输效率(单位时间内的运输量)逐步提高.故选B.]
达标检测
1.解析: (1)根据导数的几何意义知正确.
(2)若|f (x0)|越大,瞬时变化率越大,故错误.
(3)根据导函数的定义知正确.
(4)若f ′(x0)=0说明曲线在x=x0处切线平行于x轴,不能说不存在.
[答案] (1)√ (2)× (3)√ (4)×
2.C [由题意可得: = =f ′(1),
即: =×2=1.故应选C.]
3. B 解析:由导数的几何意义,f ′(xA),f ′(xB)分别是切线在点A、B处切线的斜率,
由图象可知f ′(xA)<f ′(xB).
4.A 解析:由题意,知k=y′|x=0= =1,
∴a=1.又点(0,b)在切线上,∴b=1,故选A.
5. [解] 设切点P(m,n),切线斜率为k,
由y′= = = (4x+2Δx)=4x,
得k=y′|x=m=4m.
由题意可知4m=8,∴m=2.
代入y=2x2-7得n=1.
故所求切点P为(2,1).
