高中数学人教B版(2019)必修第二册 4.1.1实数指数幂及其运算课件(共22张PPT)
文档属性
| 名称 | 高中数学人教B版(2019)必修第二册 4.1.1实数指数幂及其运算课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 446.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-30 00:00:00 | ||
图片预览








文档简介
(共22张PPT)
第四章 指数函数、对数函数与幂函数
4.1.1 实数指数幂及其运算
情境与问题
国家统计局有关数据显示,我国科研和开发机构基础研究经费支出近些年呈爆炸式增长:2013年为221.59亿元,2014年、2015年、2016年的年增长率分别为16.84%,14.06%,14.26%。
你能根据这三个年增长率的数据,算出年平均增长幸,并以2013年的经费支出为基础,预测2017年及以后各年的经费支出吗?
一、有理指数幂
初中我们已经学习了整数指数幂的知识,例如25=2×2×2×2×2=32,
30=
一般地,an中的a称为 ,n称为
整数指数幂运算的运算法则有
aman= ,(am)n= ,(ab)m= .
1
底数
指数
am+n
amn
ambm
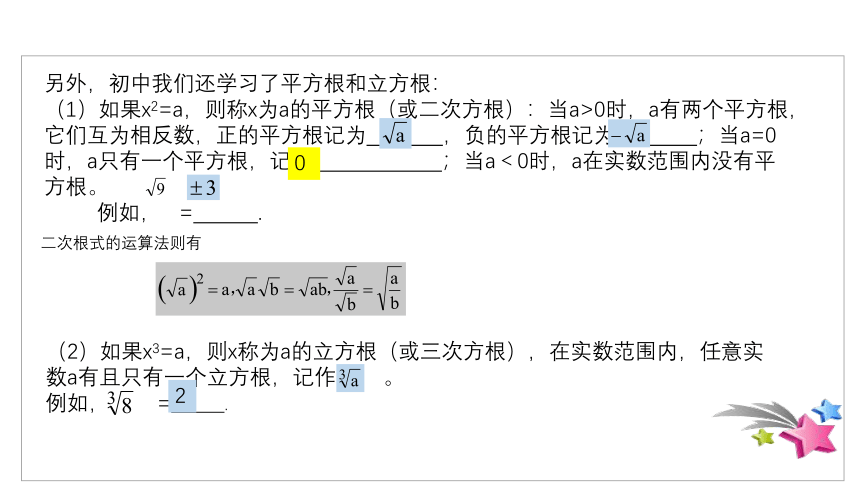
另外,初中我们还学方根和立方根:
(1)如果x2=a,则称x为a的平方根(或二次方根):当a>0时,a有两个平方根,它们互为相反数,正的平方根记为 ,负的平方根记为 ;当a=0时,a只有一个平方根,记为 ;当a<0时,a在实数范围内没有平方根。
例如, = .
二次根式的运算法则有
0
(2)如果x3=a,则x称为a的立方根(或三次方根),在实数范围内,任意实数a有且只有一个立方根,记作 。
例如, = .
2
类比二次方根和三次方根,给出四次方根和五次方根的定义。
尝试与发现
一般地,给定大于1的正整数n和实数a,如果存在实数x,使得
xn=a,
则x称为a的 。
n次方根
例如,因为方程x4=81的实数解为3与-3,因此3与-3都是81的4次方根:因为25=32,而且x5=32只有一个实数解,所以32的5次方根为2
根据方程xn=a解的情况不难看出:
(1)0的任意正整数次方根均为0,记为 .
(2)正数a的偶次方根有两个,它们互为相反数,其中正的方根称为a的n次算术根,记为 ,负的方根记为- ;负数的偶数次方根在实数范围内不存在,即当a<0且n为偶数时, 在实数范围内没有意义。
(3)任意实数的奇数次方根都有且只有一个,记为 。而且正数的奇数数次方根是一个正数,负数的奇数数次方根是一个负数.
当 有意义的时候, 称为根式,n称为根指数,a称为被开方数.
注意,虽然我们不知道 等的精确小数形式(计算器和计算机上给出的值都是近似值),但是按照定义,我们知道 的一些性质,比如 等.
一般地,根式具有以下性质:
(1)
(2)当n为奇数时, 当n为偶数时,
例如,
你能想出一个新的二次根式符号的表示方法,使 成为(am)n=amn的特例 , 成为ambm=(ab)m的特例吗?
尝试与发现
现在来将整数指数幂运算推广到分数指数幂运算,也就是给出 等的定义.同以前一样,我们希望推广后,有关的运算性质仍然能保持,比如(am)n=amn在m,n都是分数时仍然成立,因此, 应该满足
这表示 应该是 5 的平方跟,但是5的平方根有两个,即 和- ,为了方便起见,我们规定 = .这样一来,尝试与发现中的问题也就解决了.
一般地,如果n是正整数,那么:当 有意义时,规定
当 没有意义时,称 没有意义.
例如,
而 没有意义,因为 没有意义.
2
-3
这样一来, 可以看成 ,也可以看成 ,即
= =
对于一般的正分数 ,也可作类似规定,即
但值得注意的是,这个式子在 不是既约分数(即m,n有大于1的公约数)时可能会有歧义.
例如, 是有意义的,而 是没有意义的。因此,以后如果没有特别说明,一般总认为分数指数幂中的指数都是既约分数。
负分数指数幂的定义与负整数指数幂类似,即若s是正分数,as有意义且a≠0时,规定a- s=
现在我们已经将整数指数幂推广到了分数指数幂(即有理数指数幂).
一般情况下,当s与都是有理数时,有运算法则:
asat=as+t
(as)t=ast
(ab)s=asbs
例如,
典型例题
例1 求证:如果a>b>0,n是大于1的自然数,那么
证明 假设 ,即
或
根据不等式的性质与根式的性质,得
a这都与a>b矛盾,因此假设不成立,从而
利用例1的结论,可以证明(留作练习):
(1)如果a>s>0,s是正有理数,那么as>bs;
(2)如果a>1,s是正有理数,那么as>1,a-s<1;
(3)如果a>1,s>t>0,且s与t均为有理数,那么as>at
二、实数指数幂
有理数指数幂还可以推广到无理数指数幂,下面我们通过一个例子来描述其中的思想。
应该怎样理解2π这个数呢
尝试与发现
根据前面的知识,猜测2π与23的相对大小,以及2π与24的相对大小
不难猜出,23<2π<24.
就像在计算圆的面积时,我们常常取π为3.14一样,在精度要求不高的前提下,我们可以认为
2π≈23.14=
因为π=3.141592653...是一个无理数(即无限不循环小数),我们写不出他的精确的小数形式,但是因为3.1<π<3.2,所以23.1<2π<23.2,同样
3.14<π<3.15 23.14<2π<23.15
3.141<π<3.142 23.141<2π<23.142
3.1415<π<3.1416 23.1415<2π<23.1416
3.14159<π<3.14160 23.14159<2π<23.14160
也就是说,两个序列
3.1,3.14,3.141,3.1415,3.14159,...;
3.2.,3.15,3.142,3.1416,3.14160,...
中的数,随着小数点后位数的增加,都越来越接近,从而两个序列
23.1,23.14,23.141,23.1415,23.14159,...;
23.2,23.15,23.142,23.1416,23.14160,...;
中的数,随着指数的变化,也都会越来越接近一个实数,这个实数就是2π
一般地,当a>0且t是无理数时,at都是一个确定的实数,我们可以用与上述类似的方法找出它的任意精度的近似值。因此,当a>0,t为任意实数时,可以认为实数指数幂at都有意义.
可以证明,对任意实数s和t,类似前述有理指数释的运算法则仍然成立。
典型例题
例2 计算下列各式的值:
(1)
(2)
典型例题
例3 化简下列各式:
(1)
(2)
三、用信息技术求实数指数幂
实数指数幂的值可以通过计算器或计算机软件方便地求得.
在GeoGebra中,在“运算区”利用符号“ ”,就可以得到实数指数幂的精确值或近似值.如下图所示,前面三个是在符号计算模式下的输入和所得到的结果,后面两个是在数值计算模式下得到的结果。下面我们来求本节情境与问题中的年平均增长率。
假设年平均增长率为x,则应该有
(1+16.84%)(1+14.06%)(1+14.26%)=(1+x)3
从而x=
由此可预测2017年的科研和开发机构基础研究经费支出为
221.59×(1+15.05%)4≈388.24(亿元)
其他年份的预测值可用类似的方法算出.
第四章 指数函数、对数函数与幂函数
4.1.1 实数指数幂及其运算
情境与问题
国家统计局有关数据显示,我国科研和开发机构基础研究经费支出近些年呈爆炸式增长:2013年为221.59亿元,2014年、2015年、2016年的年增长率分别为16.84%,14.06%,14.26%。
你能根据这三个年增长率的数据,算出年平均增长幸,并以2013年的经费支出为基础,预测2017年及以后各年的经费支出吗?
一、有理指数幂
初中我们已经学习了整数指数幂的知识,例如25=2×2×2×2×2=32,
30=
一般地,an中的a称为 ,n称为
整数指数幂运算的运算法则有
aman= ,(am)n= ,(ab)m= .
1
底数
指数
am+n
amn
ambm
另外,初中我们还学方根和立方根:
(1)如果x2=a,则称x为a的平方根(或二次方根):当a>0时,a有两个平方根,它们互为相反数,正的平方根记为 ,负的平方根记为 ;当a=0时,a只有一个平方根,记为 ;当a<0时,a在实数范围内没有平方根。
例如, = .
二次根式的运算法则有
0
(2)如果x3=a,则x称为a的立方根(或三次方根),在实数范围内,任意实数a有且只有一个立方根,记作 。
例如, = .
2
类比二次方根和三次方根,给出四次方根和五次方根的定义。
尝试与发现
一般地,给定大于1的正整数n和实数a,如果存在实数x,使得
xn=a,
则x称为a的 。
n次方根
例如,因为方程x4=81的实数解为3与-3,因此3与-3都是81的4次方根:因为25=32,而且x5=32只有一个实数解,所以32的5次方根为2
根据方程xn=a解的情况不难看出:
(1)0的任意正整数次方根均为0,记为 .
(2)正数a的偶次方根有两个,它们互为相反数,其中正的方根称为a的n次算术根,记为 ,负的方根记为- ;负数的偶数次方根在实数范围内不存在,即当a<0且n为偶数时, 在实数范围内没有意义。
(3)任意实数的奇数次方根都有且只有一个,记为 。而且正数的奇数数次方根是一个正数,负数的奇数数次方根是一个负数.
当 有意义的时候, 称为根式,n称为根指数,a称为被开方数.
注意,虽然我们不知道 等的精确小数形式(计算器和计算机上给出的值都是近似值),但是按照定义,我们知道 的一些性质,比如 等.
一般地,根式具有以下性质:
(1)
(2)当n为奇数时, 当n为偶数时,
例如,
你能想出一个新的二次根式符号的表示方法,使 成为(am)n=amn的特例 , 成为ambm=(ab)m的特例吗?
尝试与发现
现在来将整数指数幂运算推广到分数指数幂运算,也就是给出 等的定义.同以前一样,我们希望推广后,有关的运算性质仍然能保持,比如(am)n=amn在m,n都是分数时仍然成立,因此, 应该满足
这表示 应该是 5 的平方跟,但是5的平方根有两个,即 和- ,为了方便起见,我们规定 = .这样一来,尝试与发现中的问题也就解决了.
一般地,如果n是正整数,那么:当 有意义时,规定
当 没有意义时,称 没有意义.
例如,
而 没有意义,因为 没有意义.
2
-3
这样一来, 可以看成 ,也可以看成 ,即
= =
对于一般的正分数 ,也可作类似规定,即
但值得注意的是,这个式子在 不是既约分数(即m,n有大于1的公约数)时可能会有歧义.
例如, 是有意义的,而 是没有意义的。因此,以后如果没有特别说明,一般总认为分数指数幂中的指数都是既约分数。
负分数指数幂的定义与负整数指数幂类似,即若s是正分数,as有意义且a≠0时,规定a- s=
现在我们已经将整数指数幂推广到了分数指数幂(即有理数指数幂).
一般情况下,当s与都是有理数时,有运算法则:
asat=as+t
(as)t=ast
(ab)s=asbs
例如,
典型例题
例1 求证:如果a>b>0,n是大于1的自然数,那么
证明 假设 ,即
或
根据不等式的性质与根式的性质,得
a
利用例1的结论,可以证明(留作练习):
(1)如果a>s>0,s是正有理数,那么as>bs;
(2)如果a>1,s是正有理数,那么as>1,a-s<1;
(3)如果a>1,s>t>0,且s与t均为有理数,那么as>at
二、实数指数幂
有理数指数幂还可以推广到无理数指数幂,下面我们通过一个例子来描述其中的思想。
应该怎样理解2π这个数呢
尝试与发现
根据前面的知识,猜测2π与23的相对大小,以及2π与24的相对大小
不难猜出,23<2π<24.
就像在计算圆的面积时,我们常常取π为3.14一样,在精度要求不高的前提下,我们可以认为
2π≈23.14=
因为π=3.141592653...是一个无理数(即无限不循环小数),我们写不出他的精确的小数形式,但是因为3.1<π<3.2,所以23.1<2π<23.2,同样
3.14<π<3.15 23.14<2π<23.15
3.141<π<3.142 23.141<2π<23.142
3.1415<π<3.1416 23.1415<2π<23.1416
3.14159<π<3.14160 23.14159<2π<23.14160
也就是说,两个序列
3.1,3.14,3.141,3.1415,3.14159,...;
3.2.,3.15,3.142,3.1416,3.14160,...
中的数,随着小数点后位数的增加,都越来越接近,从而两个序列
23.1,23.14,23.141,23.1415,23.14159,...;
23.2,23.15,23.142,23.1416,23.14160,...;
中的数,随着指数的变化,也都会越来越接近一个实数,这个实数就是2π
一般地,当a>0且t是无理数时,at都是一个确定的实数,我们可以用与上述类似的方法找出它的任意精度的近似值。因此,当a>0,t为任意实数时,可以认为实数指数幂at都有意义.
可以证明,对任意实数s和t,类似前述有理指数释的运算法则仍然成立。
典型例题
例2 计算下列各式的值:
(1)
(2)
典型例题
例3 化简下列各式:
(1)
(2)
三、用信息技术求实数指数幂
实数指数幂的值可以通过计算器或计算机软件方便地求得.
在GeoGebra中,在“运算区”利用符号“ ”,就可以得到实数指数幂的精确值或近似值.如下图所示,前面三个是在符号计算模式下的输入和所得到的结果,后面两个是在数值计算模式下得到的结果。下面我们来求本节情境与问题中的年平均增长率。
假设年平均增长率为x,则应该有
(1+16.84%)(1+14.06%)(1+14.26%)=(1+x)3
从而x=
由此可预测2017年的科研和开发机构基础研究经费支出为
221.59×(1+15.05%)4≈388.24(亿元)
其他年份的预测值可用类似的方法算出.
