3.1.1 椭圆的简单几何性质(2)(共16张PPT)
文档属性
| 名称 | 3.1.1 椭圆的简单几何性质(2)(共16张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-30 11:33:21 | ||
图片预览





文档简介
(共16张PPT)
3.1椭圆
3.1.1椭圆的几何性质(2)
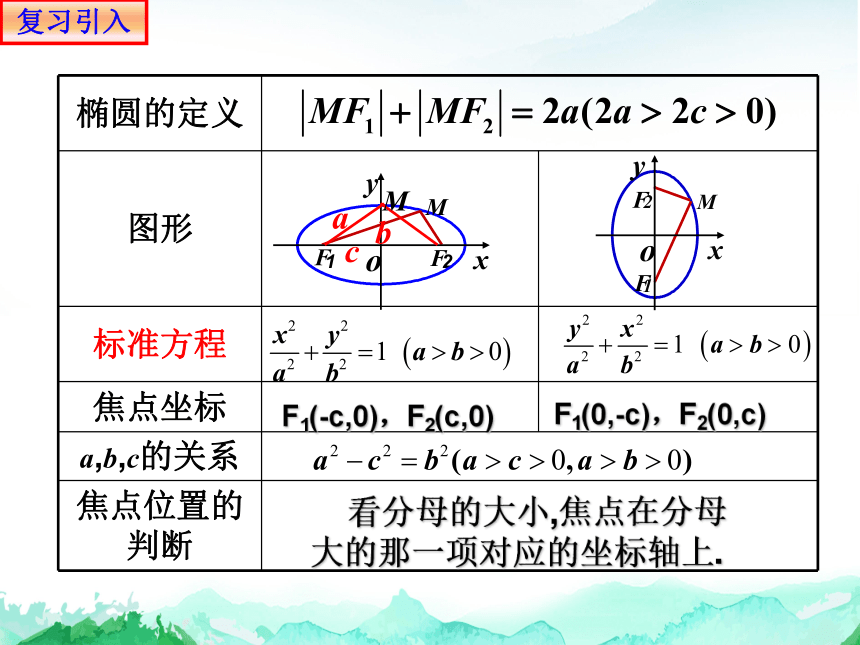
椭圆的定义
图形
标准方程
焦点坐标
a,b,c的关系
焦点位置的判断
F1(-c,0),F2(c,0)
F1(0,-c),F2(0,c)
看分母的大小,焦点在分母大的那一项对应的坐标轴上.
1
2
y
o
F
F
M
x
1
o
F
y
x
2
F
M
c
a
b
M
复习引入
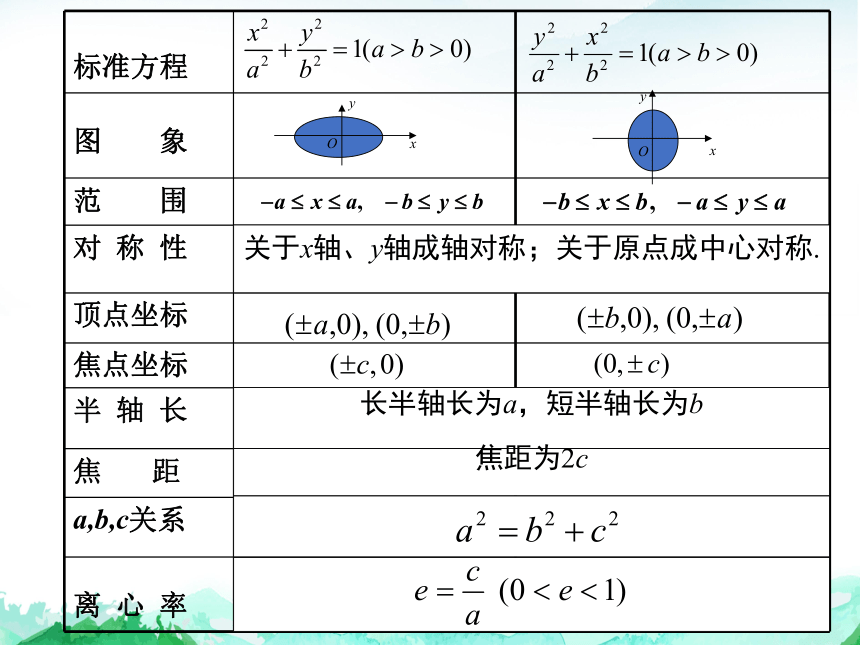
标准方程
范围
对称性
顶点坐标
焦点坐标
半轴长
离心率
a、b、c的关系
-a≤x≤ a, -b≤y≤ b
关于x 轴、y 轴成轴对称;关于原点成中心对称
(a,0)、(-a,0)、(0,b)、(0,-b)
(c,0)、(-c,0)
长半轴长为a,短半轴长为b. a>b
a2=b2+c2
标准方程
图 象
范 围
对 称 性
顶点坐标
焦点坐标
半 轴 长
焦 距
a,b,c关系
离 心 率
关于x轴、y轴成轴对称;
关于原点成中心对称.
长半轴长为a,
短半轴长为b
焦距为2c
x
y
O
x
y
O
关于x轴、y轴成轴对称;
关于原点成中心对称.
长半轴长为a,
短半轴长为b
焦距为2c
关于x轴、y轴成轴对称;关于原点成中心对称.
长半轴长为a,短半轴长为b
.
焦距为2c
典型例题
例1如图,一种电影放映灯的反射镜面是旋转椭圆面(椭圆绕其对称轴旋转一周形成的曲面)的一部分.过对称轴的截口BAC是椭圆的一部分,灯丝位于椭圆的一个焦点F1上,片门位于另一个焦点F2上.由椭圆一个焦点F1发出的光线,经过旋转椭圆面反射后集中到另一个焦点F2.已知BC⊥F1F2,|F1B|=2.8cm,
| F1F2 |=4.5cm.试建立适当的平面直角坐标系,求截口BAC所在椭圆的方程(精确到0.1cm).
典型例题
例1如图,一种电影放映灯的反射镜面是旋转椭圆面(椭圆绕其对称轴旋转一周形成的曲面)的一部分.过对称轴的截口BAC是椭圆的一部分,灯丝位于椭圆的一个焦点F1上,片门位于另一个焦点F2上.由椭圆一个焦点F1发出的光线,经过旋转椭圆面反射后集中到另一个焦点F2.已知BC⊥F1F2,|F1B|=2.8cm,
| F1F2 |=4.5cm.试建立适当的平面直角坐标系,求截口BAC所在椭圆的方程(精确到0.1cm).
H
d
例题讲评
新知探究
O
x
y
F
H
M
l
新知探究
F1
O
F2
x
y
M
N
F1
O
F2
x
y
M
椭圆上的点到椭圆一个焦点的距离叫做椭圆的焦半径,上述结果就是椭圆的焦半径公式.
|MF1|=a+ex0
|MF2|=a-ex0
|MF2|=a-ey0
|MF1|=a+ey0
x
F1
F2
y
O
M
新知探究
(±a,0)
a
(0, ±b)
b
(-a,0)
a+c
(a,0)
a-c
椭圆上一点M(x0,y0)到左焦点F1(-c,0) 和右焦点F2(c,0)的距离分别是
|MF1|=a+ex0
|MF2|=a-ex0
新知探究
课堂小结
标准方程
范围
对称性
顶点坐标
焦点坐标
半轴长
离心率
a,b,c的关系
|x|≤ a,|y|≤ b
关于x轴、y轴成轴对称;关于原点成中心对称
(a,0)、(-a,0)、(0,b)、(0,-b)
(c,0)、(-c,0)
长半轴长为a,短半轴长为b. a>b
a2=b2+c2
|x|≤ b,|y|≤ a
(b,0)、(-b,0)、(0,a)、(0,-a)
(0 , c)、(0, -c)
F1
O
F2
x
y
M
椭圆上的点到椭圆一个焦点的距离叫做椭圆的焦半径,上述结果就是椭圆的焦半径公式.
|MF1|=a+ex0
|MF2|=a-ex0
课堂小结
|MF2|=a-ey0
|MF1|=a+ey0
x
F1
F2
y
O
M
巩固练习
习题3.1:课本P115
5,6,8,10,13,14 .
谢谢大家
再见!
3.1椭圆
3.1.1椭圆的几何性质(2)
椭圆的定义
图形
标准方程
焦点坐标
a,b,c的关系
焦点位置的判断
F1(-c,0),F2(c,0)
F1(0,-c),F2(0,c)
看分母的大小,焦点在分母大的那一项对应的坐标轴上.
1
2
y
o
F
F
M
x
1
o
F
y
x
2
F
M
c
a
b
M
复习引入
标准方程
范围
对称性
顶点坐标
焦点坐标
半轴长
离心率
a、b、c的关系
-a≤x≤ a, -b≤y≤ b
关于x 轴、y 轴成轴对称;关于原点成中心对称
(a,0)、(-a,0)、(0,b)、(0,-b)
(c,0)、(-c,0)
长半轴长为a,短半轴长为b. a>b
a2=b2+c2
标准方程
图 象
范 围
对 称 性
顶点坐标
焦点坐标
半 轴 长
焦 距
a,b,c关系
离 心 率
关于x轴、y轴成轴对称;
关于原点成中心对称.
长半轴长为a,
短半轴长为b
焦距为2c
x
y
O
x
y
O
关于x轴、y轴成轴对称;
关于原点成中心对称.
长半轴长为a,
短半轴长为b
焦距为2c
关于x轴、y轴成轴对称;关于原点成中心对称.
长半轴长为a,短半轴长为b
.
焦距为2c
典型例题
例1如图,一种电影放映灯的反射镜面是旋转椭圆面(椭圆绕其对称轴旋转一周形成的曲面)的一部分.过对称轴的截口BAC是椭圆的一部分,灯丝位于椭圆的一个焦点F1上,片门位于另一个焦点F2上.由椭圆一个焦点F1发出的光线,经过旋转椭圆面反射后集中到另一个焦点F2.已知BC⊥F1F2,|F1B|=2.8cm,
| F1F2 |=4.5cm.试建立适当的平面直角坐标系,求截口BAC所在椭圆的方程(精确到0.1cm).
典型例题
例1如图,一种电影放映灯的反射镜面是旋转椭圆面(椭圆绕其对称轴旋转一周形成的曲面)的一部分.过对称轴的截口BAC是椭圆的一部分,灯丝位于椭圆的一个焦点F1上,片门位于另一个焦点F2上.由椭圆一个焦点F1发出的光线,经过旋转椭圆面反射后集中到另一个焦点F2.已知BC⊥F1F2,|F1B|=2.8cm,
| F1F2 |=4.5cm.试建立适当的平面直角坐标系,求截口BAC所在椭圆的方程(精确到0.1cm).
H
d
例题讲评
新知探究
O
x
y
F
H
M
l
新知探究
F1
O
F2
x
y
M
N
F1
O
F2
x
y
M
椭圆上的点到椭圆一个焦点的距离叫做椭圆的焦半径,上述结果就是椭圆的焦半径公式.
|MF1|=a+ex0
|MF2|=a-ex0
|MF2|=a-ey0
|MF1|=a+ey0
x
F1
F2
y
O
M
新知探究
(±a,0)
a
(0, ±b)
b
(-a,0)
a+c
(a,0)
a-c
椭圆上一点M(x0,y0)到左焦点F1(-c,0) 和右焦点F2(c,0)的距离分别是
|MF1|=a+ex0
|MF2|=a-ex0
新知探究
课堂小结
标准方程
范围
对称性
顶点坐标
焦点坐标
半轴长
离心率
a,b,c的关系
|x|≤ a,|y|≤ b
关于x轴、y轴成轴对称;关于原点成中心对称
(a,0)、(-a,0)、(0,b)、(0,-b)
(c,0)、(-c,0)
长半轴长为a,短半轴长为b. a>b
a2=b2+c2
|x|≤ b,|y|≤ a
(b,0)、(-b,0)、(0,a)、(0,-a)
(0 , c)、(0, -c)
F1
O
F2
x
y
M
椭圆上的点到椭圆一个焦点的距离叫做椭圆的焦半径,上述结果就是椭圆的焦半径公式.
|MF1|=a+ex0
|MF2|=a-ex0
课堂小结
|MF2|=a-ey0
|MF1|=a+ey0
x
F1
F2
y
O
M
巩固练习
习题3.1:课本P115
5,6,8,10,13,14 .
谢谢大家
再见!
